Проверка гипотез о числовых значениях параметров

Гипотезы о числовых значениях встречаются в различных задачах. Пусть х_х (i =1,2,…, п) — значения некоторого параметра изделий, производящихся станком автоматической линии, и пусть а — заданное номинальное значение этого параметра. Каждое отдельное значение x_i может, естественно, как-то отклоняться от заданного номинала. Очевидно, для того, чтобы проверить правильность настройки этого станка, надо убедиться в том, что среднее значение параметра у производимых на нем изделий будет соответствовать номиналу, т. е. проверить гипотезу Я₀: х₀ = а против альтернативной Яр х^Фа, или Н₂: х₀<�а, или Н₂: х$>а.

При произвольной настройке станка может возникнуть необходимость проверки гипотезы о том, что точность изготовления изделий по данному параметру, задаваемая дисперсий а², равна заданной величине о$, т. е. Я₀: а² = Oq или, например, того, что доля бракованных изделий, производимых станком, равна заданной величине р₀, т. е. Я₀: р = р₀ и т. д.

Аналогичные задачи могут возникнуть, например, в финансовом анализе, когда по данным выборки надо установить, можно ли считать доходность актива определенного вида или портфеля ценных бумаг, либо ее риск равным заданному числу; или по результатам выборочной аудиторской проверки однотипных документов нужно убедиться, можно ли считать процент допущенных ошибок равным номиналу, и т. п.

В общем случае гипотезы подобного типа имеют вид Я₀: 0 = Д₀, где 0 некоторый параметр исследуемого распределения, а Д₀ — область его конкретных значений, состоящая в частном случае из одного значения.

При проверке гипотезы указанного типа можно использовать тот же подход, что и в параграф 10.2 (см., например, проверку гипотезы Я₀: а = а₀ против альтернативной Яр а = а_{> а₀ при известной дисперсии а² в примере 10.1).

Соответствующие критерии проверки гипотез о числовых значениях параметров нормального закона приведены в табл. 10.2.

Таблица 10.2.

Окончание табл. 10.2

Примечание. Критические значения статистик на уровне значимости, а определяют по соответствующим таблицам приложений исходя из соотношений:

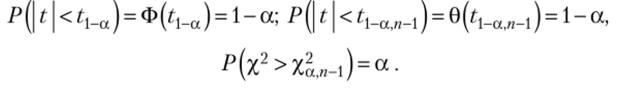
0 Пример 10.8. На основании сделанного прогноза средняя дебиторская задолженность однотипных предприятий региона должна составить «₀= 120 ден. ед. Выборочная проверка 10 предприятий дала среднюю задолженность х = 135 ден. ед., а среднее квадратическое отклонение задолженности 5 = 20 ден. ед. На уровне значимости 0,05: а) выяснить, можно ли принять данный прогноз; б) найти мощность критерия, использованного в п. а); в) определить минимальное число предприятий, которое следует проверить, чтобы обеспечить мощность критерия 0,975.

Решение, а) Проверяемая гипотеза #₀: х₀ =а₀ = 120. В качестве альтернативной возьмем гипотезу Н_{: х₀=а^ = 135. Так как генеральная дисперсия а² неизвестна, то используем^{-критерий} Стьюдента. Статистика.

х — а 135−120.

критерия в соответствии с табл. 10.2 равна t =, ,—= =—, =2,25.

s/yjn-1 20/V10−1.

Критическое значение статистики t_x_₂. o, o5;io-i⁼ %);9 ⁼ 1"83.

Так как 111 > ?_09;9 (2,25 > 1,83), то гипотеза Н₀ отвергается, т. е. на 5%-ном уровне значимости сделанный прогноз должен быть отвергнут.

б) Так как а_{ = 135 > а₀ = 120, то критическая область правосторонняя и критическое значение выборочной средней.

т.е. критическая область значений для х есть интервал (132,2; +). Мощность критерия (см. параграф 10.2) равна вероятности Р отвергнуть гипотезу Н₀, когда верна гипотеза #_t, т. е.

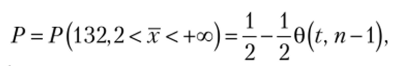
где 0 (?, п — 1) — функция, выражающая вероятность попадания случайной величины, имеющей^{-распределение} Стъюдента, на отрезок (-1, t)

(аналогична функции Лапласа для нормального распределения (см. параграф 9.7));

По табл. IV приложений^[1] 0 (-0,42; 9) = -0 (0,42; 9) ~ -0,31.

Итак, Р = |-|е (-0,42;9)Л (1 + 0,31)~0,6б.

в) Воспользуемся решением примера 10.1, б), в котором формула <10.1') объема выборки была получена для случая нормального закона распределения х, когда известна генеральная дисперсия а^[2]. Так как у нас а^[2] не известна, а известна лишь ее выборочная оценка s^[2], то статистика Крите;

рия t = ——. ⁰ имеет^{-распределение} Стьюдента (см. табл. 10.2), и соот- s / v п —1.

ветствующая скорректированная формула (10.Г) для п примет вид.

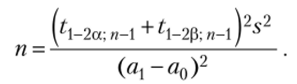
При, а = 0,05, р = 0,025 (ибо по условию мощность критерия 1 — р = 0,975), а₀ = 120, а_х = 135, s = 20 получим:

Так как правая часть равенства сама зависит от неизвестного значения п, то п находится приближенно подбором. Так, при п = 20, п = 30 равенство (*) не выполняется (например, при п = 20.

• 20 *y (t₀, 9;₁₉ + W>)^[2] =у (1,⁷³ +2,09)2 = 24,7), а при п = 25
• 25 * у (*о, 9;24 + W)^[2] =у (1,71 + 2,06)^[2] = 25,3.

Следовательно, необходимо проверить 25 предприятий. ?

Аналогично проверяются и другие гипотезы о числовых значениях параметров в соответствии с критериями проверки, приведенными в табл.

10.2.

При проверке статистических гипотез есть идругой подход, основанный на том, что выше (в параграфе 9.3) для параметров х₀, р, а² были построены доверительные интервалы. И если параметр х₀ (или р, или а²) не попадает в доверительный интервал с надежностью у = 1-а, т. е. попадает в критическую область, то гипотеза Я₀ отвергается; в противном случае полагают, что имеющиеся данные не противоречат гипотезе Я₀.

Достоинством такого подхода, основанного на построении доверительного интервала для параметра, является то, что кроме проверки гипотезы Я₀ получается дополнительная информация о возможных истинных значениях параметра. Однако этот подход применим, если в качестве конкурирующих выступают гипотезы типа х₀Фа, рф р₀, о² *, предполагающие выбор двусторонней критической области.

0 Пример 10.9. По данным примера 9.10 на уровне значимости а ~ 0,05 проверить гипотезу о том, что средняя выработка рабочих всего цеха равна 121%.

Решение. Проверяемая гипотеза Я₀: д:₀ = 121(%). Конкурирующая гипотеза Я: х₀Ф12. В примере 9.10 с надежностью у~ 1 — 0,05 = 0,95 построен доверительный интервал для Т₀: 117,33 < х₀ < 121,07. Так как значение а = 121 принадлежит этому интервалу, то гипотеза Я₀ не отвергается, т. е. имеющиеся данные не противоречат предположению о том, что средняя выработка рабочих равна 121%. ?

О Пример 10.10. По данным примера 9.11 на уровне значимости, а = 0,05 проверить гипотезу о том, что доля нестандартных деталей во всей партии равна 12%.

Решение. Проверяемая гипотеза Я₀: р = 0,12 (или 12%). Конкурирующая гипотеза Я: рФ0,12. В примере 9.11 с надежностью у = 1 — 0,05 = 0,95 построен доверительный интервал для р: 0,044 < р < 0,116. Так как значение р₀= 0,12 не принадлежит этому интервалу, то на уровне значимости, а = 0,05 гипотеза Я₀ отвергается, т. е. имеющиеся данные не позволяют считать, что в партии находится 12% нестандартных деталей. ?

1> Пример 10.11. По данным примера 9.17 па уровне значимости а — 0,1 проверить гипотезу о том, что среднее квадратическое отклонение суточной выработки работниц равно 20 м/ч.

Решение. Проверяемая гипотеза Я₀: а² = 20²=400. Конкурирующая гипотеза Я: а² *400. В примере 9.17 с надежностью у = 1−0,1 = 0,9 получен доверительный интервал для о²: 157,3 < а² <468,9. Так как значение Gjj =400 принадлежит этому интервалу, то на уровне значимости, а = 0,1 гипотеза Я₀ нс отвергается, т. е. имеющиеся данные не противоречат предположению о том, что среднее квадратическое отклонение суточной выработки работниц равно 20 м/ч. ?

• [1] Так как непосредственно значений 0(f, п) в данной таблице нет, «внутри» ее в строкеk = 9 находим близкие к 0,42 значения 0,40 и 0,54, соответствующие вероятностям у = 0,3
• [2] и у = 0,4, т. е. 0(0,40; 9) = 0,3, и 0(0,54; 9) = 0,4, а искомое значение 0(0,42; 9) «0,31 находиминтерполированием.
• [3] и у = 0,4, т. е. 0(0,40; 9) = 0,3, и 0(0,54; 9) = 0,4, а искомое значение 0(0,42; 9) «0,31 находиминтерполированием.
• [4] и у = 0,4, т. е. 0(0,40; 9) = 0,3, и 0(0,54; 9) = 0,4, а искомое значение 0(0,42; 9) «0,31 находиминтерполированием.
• [5] и у = 0,4, т. е. 0(0,40; 9) = 0,3, и 0(0,54; 9) = 0,4, а искомое значение 0(0,42; 9) «0,31 находиминтерполированием.
• [6] и у = 0,4, т. е. 0(0,40; 9) = 0,3, и 0(0,54; 9) = 0,4, а искомое значение 0(0,42; 9) «0,31 находиминтерполированием.
• [7] и у = 0,4, т. е. 0(0,40; 9) = 0,3, и 0(0,54; 9) = 0,4, а искомое значение 0(0,42; 9) «0,31 находиминтерполированием.