Проверка значимости уравнения регрессии. 
Интервальная оценка параметров парной модели

Проверить значимость уравнения регрессии — значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В гл. 11 дисперсионный анализ рассмотрен как самостоятельный инструмент (метод) статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.

Согласно основной идее дисперсионного анализа (см. гл. 11) или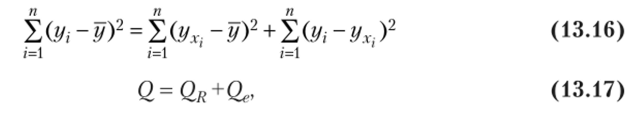

где Q — общая сумма квадратов отклонений зависимой переменной от средней, a Q_R и — соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов.

Убедимся в том, что пропущенное в равенстве (13.17) третье слагаемое.

п

Q₃ =2Yj (y_x ~y)iVi ~Ух) Р^авн0 нулю. Учитывая уравнение (13.7) и первое 1=1.

уравнение системы (12.11), имеем:

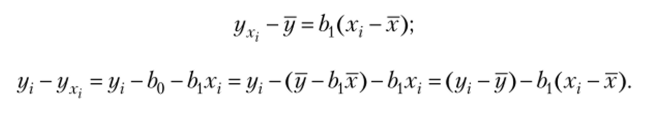
Теперь.

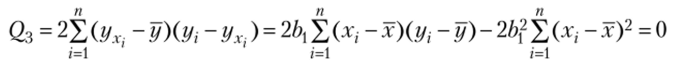
(с учетом соотношения (13.10)).

Схема дисперсионного анализа имеет вид, представленный в табл. 13.3.

Таблица 13.3.

Средние квадраты и s² (см. табл. 13.3) представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленной соответственно регрессией или объясняющей (ими) переменной (ыми) X и воздействием неучтенных случайных факторов и ошибок; т — число оцениваемых параметров уравнения регрессии; п — число наблюдений.

Замечание. При расчете общей суммы квадратов полезно иметь в виду, что.

(формула (13.17') следует из разложения.

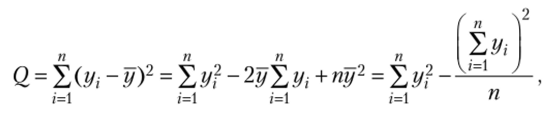
п.

1у, учитывая, что у = ——).

/2.

При отсутствии линейной зависимости между зависимой и объясняющей (ими) переменной (ыми) случайные величины s=Q_R / (т-1) и s²=Q_e/(n-m) имеют^{-распределение} соответственно ст-1ип-т

степенями свободы, а их отношение — F-распределение с теми же степенями свободы (см. параграф 4.9). Поэтому уравнение регрессии значимо на уровне а, если фактически наблюдаемое значение статистики.

где F_ajt_{ji₂ — табличное значение /'-критерия Фишера — Снедекора, определенное на уровне значимости а при k_x-m — wk₂-n — т степенях свободы.

Учитывая смысл величин sf_{ и s², можно сказать, что значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.

В случае линейной парной регрессии т = 2 и уравнение регрессии значимо на уровне а, если.

Выше (параграф 12.6) введен индекс корреляции R (для парной линейной модели — коэффициент корреляции г), выраженный через дисперсии (см. формулу (12.60)). Тог же коэффициент в терминах «сумм квадратов» примет вид.

Следует отметить, что значимость уравнения парной линейной регрессии может быть проверена и другим способом, если оценить значимость коэффициента регрессии /;, что означает проверку нулевой гипотезы о равенстве параметра Р, парной модели (13.2) нулю, т. е. Я₀: Р, =0 против альтернативной гипотезы¹ Яр Р] Ф 0.

Можно показать, что при выполнении предпосылки 5 регрессионного.

b -р анализа (с. 407) статистика? = —— имеет стандартный нормальный.

^а*,.

закон распределения Щ0; 1), а если в выражении (13.11) для о_й) заменить параметр о² его оценкой s², то статистика.

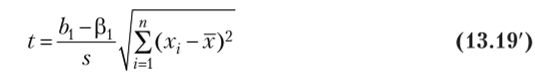
имеет^{распределение} с k = п — 2 степенями свободы. Поэтому коэффициент регрессии Ь_х значим на уровне, а (гипотеза Я₀ отвергается), если М=-Л>; -х)² >?]__а."_2, а доверительный интервал для Р, имеет вид s V /=1.

Здесь и далее используем двусторонние критерии проверки гипотез.

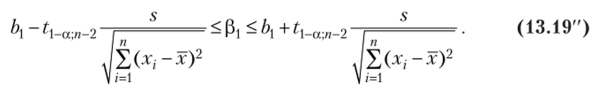
Для парной регрессионной модели оценка значимости уравнения регрессии по /•-критерию равносильна оценке значимости коэффициента регрессии Ь_х либо коэффициента корреляции г по /-критерию (см. параграф 12.5), ибо эти критерии связаны соотношением F = t². А интервальные оценки для параметра Р, (13.19″) — при нормальном законе распределения зависимой переменной и Р_(/Л. = Pi (12.51) совпадают.

При построении доверительного интервала для дисперсии возмущений с² исходят из того, что статистика —— имеет^{-распределение} с k = п — 2

а¹

степенями свободы. Поэтом}' интервальная оценка для а² на уровне значимости, а имеет вид (см. формулу (9.47)):

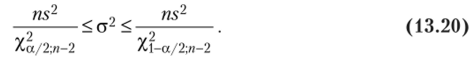
|> Пример 13.2. По данным табл. 13.1 оценить на уровне, а = 0,05 значимость уравнения регрессии Y по X Найти интервальную оценку для параметров Р, и а².

ю.

Решение. 1-й способ. Выше, в примере 13.1, были найдены ^г/,=68, ю 1=1.

Хг/,² = 496.

Вычислим необходимые суммы квадратов по формулам (13.16),.

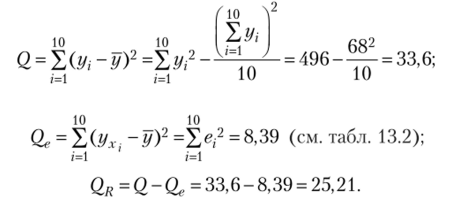
(13.17):

По формуле (13.18') F=^25,2^ ²⁾ = 24,04.

По таблице F-распределения (табл. VI приложений) F₀₀₅._V8 = 4,20. Таккак F> F₀ 05;i_;8, то уравнение регрессии значимо.

• 1°
• 2-й способ. Учитывая, что Ь_{ = 1,016, ?(*,•-х)² = 24,40, s² = 1,049 (см.

пример 13.1, табл. 13.2), по формуле (13.19') /= !'^^-J24,40 =4,90.

VI, 049.

По таблице^{-распределения} (табл. IV приложений) ?q, 95;8 ⁼ 2,31. Так как t >^о, 95;8'^то коэффициент регрессии, а значит, и уравнение парной линейной регрессии Y по X значимы. Оба способа оценки значимости уравнения парной регрессии равносильны, ибо F=t² (24,40 = 4,90²).

Найдем 100 (1 — а) = 95%-ный доверительный интервал для параметра p_t. По формуле (13.19″).

или 0,537 < Pj < 1,495, т. е. с надежностью 0,95 при изменении мощности пласта X на 1 м суточная выработка Y будет изменяться на величину, заключенную в интервале от 0,537 до 1,495 (т).

Найдем 95%-ный интервал для параметра сг.

Учитывая, что, а = 1 — 0,95 = 0,05, найдем по табл. V приложений Х"/2;и-2⁼ = Хо, 025:8= ¹⁷-⁵³; Xi-_a/2;n-2=Xo, 975;8 = ²'¹⁸' ^По Формуле (13.20).

Таким образом, с надежностью 0,95 дисперсия возмущений заключена в пределах от 0,599 до 4,81, а их стандартное отклонение — от 0,774 до 2,19 (т). ?