Многомерные модели ротатабельных ЦКП

Определение. План порядка d называется ротатабельным, если дисперсия оценки функции отклика ц = (х_1; х₂, …, х_к).

вточке (х_1;х₂, зависит лишь от расстояния р (х, х_2> …, х^).

этой точки до центра плана и не зависит от ее положения на гиперсфере.

Таким образом, план ^(N) по определению будет ротатабельным порядка d, если.

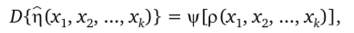
к.

гдер² = р²(Х], х₂, …, х_к) = 1х².

i=i.

В общем виде необходимые и достаточные условия существования ротатабельных планов произвольного порядка выглядят следующим образом.

Пусть D = (x_iu) (i = 1, …, fc; и = 1, …, N) — матрица плана ?(ЛГ) порядка d, а X = (x_JU) (j = 0, 1, …, р; и = 1, …, N) — матрица независимых переменных ранга р + 1, соответствующая этому плану. План ^ (АО будет ротатабельным тогда и только тогда, когда матрица Х’Х будет инвариантна относительно ортогонального преобразования R матрицы плана D. Под инвариантностью матрицы Х¹Х относительно ортогонального преобразования R матрицы плана D понимается условие.

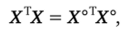
гдеХ⁰— матрица независимых переменных, соответствующая матрице планаD₀ =DR и той же функции отклика, что и матрицах [4].

Общий вид матрицы X представлен в табл. 4.22.

Таблица 4.22. Общий вид матрицы X

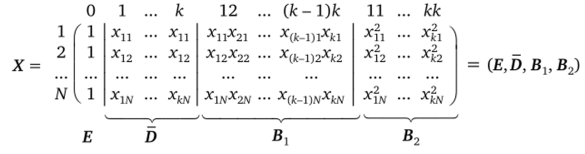
Элемент матрицы X ^хХ называется моментом. Момент считается нечетным, если в его выражении содержится хотя бы один сомножитель в нечетной степени вида xf"⁺¹ (Z = 0, 1).

Необходимое и достаточное условие ротатабельности планов второго порядка выполняется, если все нечетные моменты вплоть до четвертого порядка равны нулю, а четные соответственно равны.

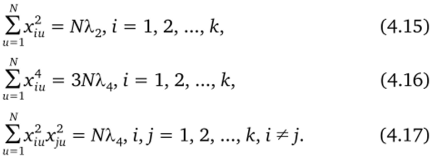
Параметр Х₂ определяется из условия выбора масштаба плана, а Х₄ выбирается с учетом некоторых ограничений. Таким образом, следует,_что матрицы D, В₁ и В₂ будут взаимно ортогональны [4], т. е. D ‘В_г = О;D 'В₂ = 0; В В₂ = 0, где 0 — нулевая матрица. Также будет выполняться условие симметрии плана E’D = 0.

Следовательно, нормированная информационная матрица ротатабельного плана второго порядка имеет вид, представленный в табл. 4.23.

Таблица 4.23. Нормированная информационная матрица ротатабельного плана второго порядка.

Чтобы матрица Х^ТХ была невырожденной, должно выполняться условие.

Существует связь между числом и радиусами гиперсфер, на которых лежат точки ротатабельного плана, с одной стороны, и параметрами Х₂ и Х_л, с другой. Суммируя по i равенство (4.15).

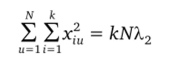
к.

и используя соотношение р^ = X*,², получаем.

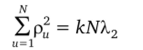
или.

где (s + 1) — число различных гиперсфер, на которых лежат точки плана; п₍₀ — число точек плана на гиперсфере радиуса р₀₎, при этом? п₀₎ = N.

Суммируя далее по; равенство (4.17) и используя (4.16), находим.

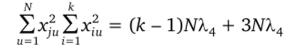
или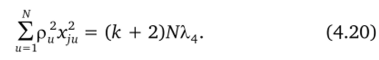

Суммируя по j равенство (4.20), получаем.

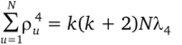
и окончательно.

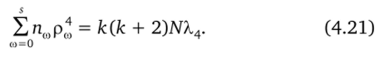
Таким образом, в соответствии с (4.19) и (4.21).

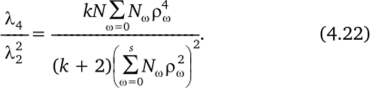
Согласно неравенству Коши [4].

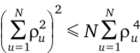
и соответственно.

Тогда равенство (4.22) с учетом последнего неравенства и (4.18) преобразуется в неравенство, и получаем ограничение на выбор параметров Х₂ и Х₄:

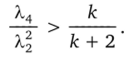
Как видно из (3.22), не существует ротатабельных планов, все точки которых расположены только на одной гиперсфере, ибо в этом случае —j- =-, т. е. матрица Х^ТХ будет вырож;

Я-2 /с «Ь 2.

денной [см. (4.18)]. Следовательно, точки ротатабельного плана должны быть расположены на концентрических гиперсферах, число которых не меньше двух. Одна из гиперсфер при этом может быть центральной точкой плана, т. е. вырожденной. В частности, если s + 1 = 2 и одна из гиперсфер вырождена (р₀ = 0), то.

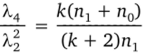
Таким образом, можно отметить следующие особенности структуры ротатабельного плана:

• • план должен удовлетворять условиям симметрии;
• • столбцы плана должны быть попарно ортогональными;
• • точки плана должны быть расположены на концентрических гиперсферах, числом не меньше двух.

Общая теория построения ротатабельных планов второго порядка является достаточно сложной. Так как задача построения ротатабельных планов не имеет однозначного решения, то рассмотрим только некоторые примеры таких планов.

Рассмотрим случай, когда число факторов к = 2. Имеет место теорема [18], что при к = 2 планы, для которых точки равнорасположены на окружности радиуса p_t ^ 0 и имеется п₀ центральных точек, будут ротатабельными тогда и только тогда, когда п₁ > 4. Таким образом, помещая точки в вершины правильного пятиугольника, шестиугольника и т. д. и добавляя к ним необходимое число центральных точек, получаем ротатабельный план 2-го порядка [4]. На рис. 4.10, а, б, в приведены примеры таких планов, последний из которых является ЦКП Бокса («звездное» плечо, а = 1,141). Матрицы этих планов.

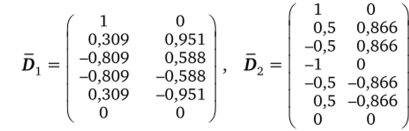
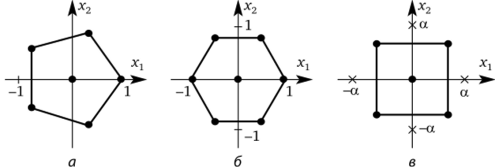
Рис. 4.10. Примеры ротатабельных планов.

Рассмотрим случай к > 2. Среди ротатабельных планов второго порядка наибольшее практическое значение имеют центральные композиционные ротатабельные планы, которые можно получить из ЦКП Бокса специальным подбором «звездного» плеча а.

Дадим правило вычисления радиусов гиперсфер для центральных композиционных ротатабельных планов, ядром которых является ПФЭ вида 2^к или ДФЭ вида 2^к~^ч (ядро плана Бокса). Первая гиперсфера вырождена (р₀ = 0). Вторая гиперсфера соответствует вписанному в нее кубу, выбранному в качестве ядра плана. Для ядрах_; = 1, следовательно, радиус этой гиперсферы pj = (х² + х + … + х,²)¹⁷² = к^]/2.

А радиус третьей гиперсферы является «звездным» плечом, который подбирается следующим образом: р₂ = а = 2^(fc_q)/4. Тем самым достигается ротатабельность плана Бокса. Следовательно, с учетом ограничений на ЦКП Бокса при к > 5 в качестве ядра ротатабельного плана можно использовать полуреплику 2^к~^г. При 5</с<7иа = 2⁽*"^1)/4 ротатабельный план будет минимальным планом Бокса. Если к > 8, ядром ротатабельного плана может служить ¹/4-реплика (а = 2^(fc₂)/4). В табл. 4.24 приведены различные варианты построения центральных композиционных ротатабельных планов второго порядка.

Таблица 4.24. Варианты построения центральных композиционных ротатабельных планов второго порядка.

В некоторых случаях радиусы второй и третьей гиперсферы совпадают pj = р₂, т. е. число гиперсфер для таких планов равно двум. Здесь предполагается, что для всех вариантов число п₀ является одинаковым. Как видно, все эти планы являются ненасыщенными — количество оцениваемых параметров меньше числа опытов.

Из рассмотренных примеров видно, что задача построения ротатабельного плана не имеет единственного решения. Но в реальных задачах проблема выбора плана, как правило, не возникает, так как обычно при проведении эксперимента существуют ограничения как на общее число опытов (число точек плана), так и на их расположение в пространстве. Также на выбор плана оказывает влияние требование к его информационному профилю.

Информацией о поверхности отклика в точке х = Qc_1; х_г,…, Хд.)^т называется величина.

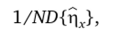
где N — число наблюдений в точках плана; D{r_x} — дисперсия оценки функции отклика в точке х. Информация представляет собой некоторую локальную меру точности оценивания функции отклика, отнесенную к одному наблюдению.

Зависимость информации от радиуса гиперсферы р = = (?xf)^½, на которой расположена точка х, и называется информационным профилем плана.

Так как Х₂ характеризует масштаб плана, то без ограничения общности можно считать, что Х.₂ = 1. Для этого случая в [4] показано, что для (4.13), используя обратную матрицу (Х'Х)^-1, можно получить.

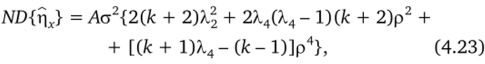
где, А = 1/{2Х₄[(к + 2) Х₄-к]}.

Выражение (4.23) можно записать в виде зависимости [4], представляющей собой информационный профиль ротатабельного плана второго порядка.

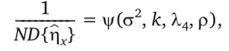
где к, а², Х_Л — параметры, определяющие профиль плана.

При заданном к и при различных Х₄ можно получить различные информационные профили. Так как Х₂ = 1, то параметр Х₄ связан с общим числом наблюдений N соотношением (4.22).

Часто интересует информация о функции отклика в некоторой окрестности центра плана. В этом случае профиль плана выбирают таким, чтобы информация была практически постоянной внутри гипершара радиуса р = 1. Такое планирование называется униформ-ротатабелъным. Для его получения достаточно обеспечить равенство дисперсии в центре плана (р = 0) и на поверхности гиперсферы радиуса р = 1. Согласно (4.23) параметр Х₄ следует взять равным положительному корню квадратного уравнения.

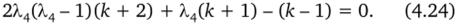
Всегда существует Х₄ такое, что Х₄ > к/(к + 2). Но при этом параметр? с₄ должен удовлетворять и условию (4.22), а обычно удовлетворить двум условиям сразу не удается, поэтому для получения униформ-ротатабельного планирования подбором числа наблюдений п₀ в центре плана добиваются того, чтобы параметр Х₄, определяемый равенством (4.22), был близок к значению, найденному из (4.24).

Рассмотрим ротатабельный план (к = 2), представленный на рис. 4.10, 6. Из (4.22) имеем.

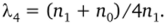
Предположим, что п₀ = 6 и щ = 6, тогда N = 12 и Х₄ = 1. Используя (4.23) и а² = 1, имеем.

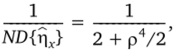
а из (4.24) для униформ-ротатабельного планирования получаем Х₄ = 0,784. При изменении числа наблюдений в центре плана п₀ изменяется его информационный профиль. Подбирая п₀, добиваемся униформ-ротатабельного планирования. На рис. 4.11 приведены соответствующие информационные профили планов.

Для параметров модели (4.2) и их дисперсий (ковариаций) при ротатабельном планировании получены следующие выражения Г4]:

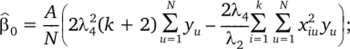
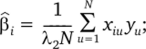
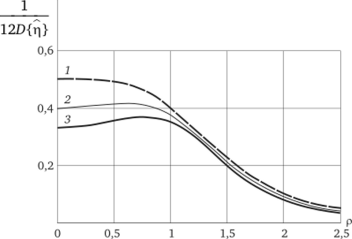
Рис. 4.11. Информационные профили планов: J — = 1 (п₀ = 6);

униформ-ротатабельное планирование: 2 — Х₄ = 0,83 (л₀ = 4);

3 — Х₄ = 0,75 (п₀ = 3).

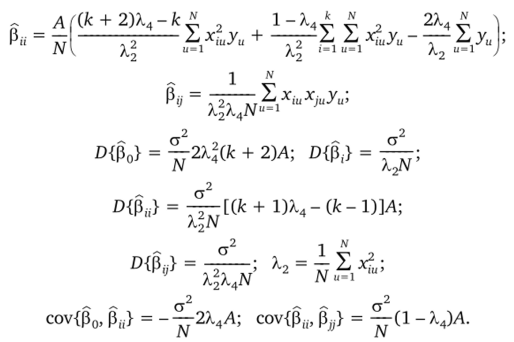
Остальные ковариации равны нулю. Эти формулы справедливы для ротатабельного планирования второго порядка при любом числе независимых переменных.

При А.₄ = 1 ротатабельное планирование оказывается почти ортогональным, не равна нулю только cov{p₀, р"}. Но от величины Х.₄ зависит вид информационного профиля плана, который для получения униформ-ротатабельного планирования требует, чтобы Х₄ была немного меньше единицы. А это приводит к дальнейшей потере ортогональности — становится отличной от нуля и соу{р_н, Ру}.

Пример 4.3.

Для случая к > 1. Для исследования к факторов рассмотрим центрально-композиционное планирование, содержащее куб + + октаэдр + п₀ центральных точек. Общее число точек равно N = 2^к + 2к + п_п. Пусть.

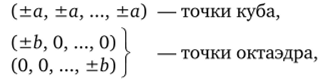
причем из условий ротатабельности b = 2^к4а. Область исследования — сфера Я. Возникает вопрос: как много центральных точек надо использовать и как выбрать размер плана, т. е. какие значения должны иметь п₀ и а? Эти вопросы эквивалентны выбору значений Х¹₂² и X, так как.

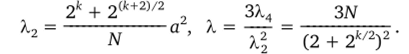
Пусть дано п₀. Тогда можно определить X, затем найти Х₂ и, наконец, определить а. В табл. 4.25 даны параметры планов для к = 2 и 0 «п₀ «12.

Таблица 4.25. Параметры для центрально-композиционного плана, когда к = 2.

Таким образом, когда экспериментатор достаточно уверен в своей модели, т. е. предполагает систематическую ошибку малой, он расширяет план. Для таких ситуаций вклад случайной составляющей значительно больше вклада, вносимого систематической ошибкой. Поэтому естественно стремиться к увеличению числа нулевых точек с тем, чтобы улучшить оценку для о²{у}. С другой стороны, если систематическая ошибка предполагается большой, то надо сузить план в области R и использовать не менее трех или четырех точек, чтобы найти некоторую оценку для а²{у}.

Проверка однородности дисперсии воспроизводимости, адекватности модели и значимости коэффициентов модели осуществляется по схеме, рассмотренной ранее.

Пусть повторные наблюдения {у_0ц}, и = 1,2, …, п₀ имеются только в центре плана. Обозначим черезу₁, у₂, y_N наблюдения в точках плана. Тогда у_0ц = у^-п₀)+и- Величина.

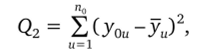
1 Л₀

где у_и = — X Уои> обусловлена дисперсией ошибок наблюдено и = 1 ния, поэтому.

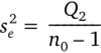
будет несмещенной оценкой дисперсии ошибок наблюдений а². Сумма квадратов, обусловленная неадекватностью модели, Qj = Q₀ — Q₂, где остаточная сумма квадратов Q₀ = У^ТУРХ^ТУ и Р = (Х^ТХ)^_1Х^ТУ. При истинности гипотезы об адекватности модели.

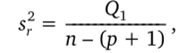
где п = N-n₀+ 1 — число различных точек плана; г = р + 1 = = (к + 1)(к + 2)/2 — число оцениваемых параметров, будет несмещенной оценкой параметра а². Гипотеза об адекватности модели отклоняется, если.

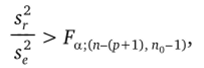
где F_a.(_n_(p₊i) ««-и — квантиль уровня, а распределения Фишера с числом степеней свободы п-(р + 1) ип₀-1.

Рассмотренное композиционное планирование представляет собой один из возможных подходов к построению ротатабельных планов второго порядка.