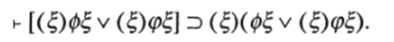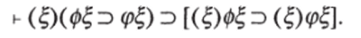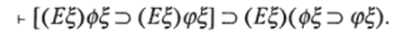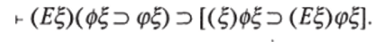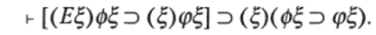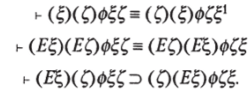Законы дистрибутивности кванторов относительно знака дизъюнкции

Из высказывания «Все вещи в универсуме круглые, или все вещи в универсуме синие» выводимо высказывание «Все вещи в универсуме круглые или синие», но обратная выводимость в общем неверна. Например, из того, что все целые числа — четные или нечетные, не следует, что все целые числа — четные, или все целые числа — нечетные. Значит, квантор общности дистрибутивен относительно знака дизъюнкции с ограничением.

Высказывание «В универсуме существует круглая или синяя вещь» эквивалентно высказыванию «В универсуме существует круглая вещь, или в универсуме существует синяя вещь». Значит, квантор существования дистрибутивен относительно знака дизъюнкции без ограничений.

Законы дистрибутивности кванторов относительно знака импликации

Из высказывания «Для каждого числа, если оно четное, оно целое» выводимо высказывание «Если каждое число четное, то каждое число целое». Но обратная выводимость в общем неверна.

Из высказывания «Если существует четное число, то существует целое число» выводимо высказывание «Существует такое число, что если оно четное, то оно целое». Но обратная выводимость в общем неверна.

Из высказывания «Существует такое число, что если оно четное, то оно целое» выводимо высказывание «Если каждое число четное, то существует целое число». Но обратная выводимость в общем неверна.

Из высказывания «Если существует четное число, то все числа целые» выводимо высказывание «Для каждого числа, если оно четное, оно целое». Но обратная выводимость в общем неверна.

Из сказанного следует, что кванторы общности и существования дистрибутивны относительно знака импликации лишь с ограничением.

Кванторы общности и существования могут переставляться в любом порядке, если они предшествуют формуле однородно, т. е. либо только кванторы общности, либо только кванторы существования. В противном случае возникает ограничение: независимый квантор существования может свободно вводиться в область действия квантора общности, но не может из нее свободно выводиться.