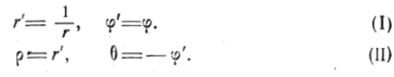Функция w = 1/z

Соответствие, даваемое этой формулой, вза* имно однозначно во всех точках плоскости, причём нулевой точке г = 0 (или 10 = 0) соответствует бесконечно удалённая точка w = — оо (или z = oo). Для исследования отображения, даваемого этой функцией, проще всего ввести полярные координаты, полагая: Z=/" *?, w=pe*. Легко видеть, что в данном, случае будет:

Опишем из нулевой точки, как центра, окружность С радиуса единица. При преобразовании (2) эта окружность переходит сама в себя, а именно каждая её точка преобразуется в симметричную точку относительно действительной оси. Преобразование (2) удобно разбить на два более простые: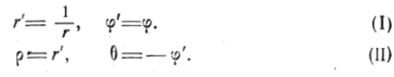

При первом из этих преобразований аргумент сохраняется, а модуль изменяется на обратный. Точка z, находящаяся внутри окружности С, преобразуется в точку w находящуюся вне окружности и лежащую на продолжении отрезка Oz, причём произведение расстояний от точки О отображённой и первоначальной точки равно единице. Такое отображение мы называем преобразованием при помощи взаимных радиусов-векторов (гл. 1, § 2, п. 5) или инверсией относительно окружности С. Точки z и w переходящие одна в другую с помощью этого преобразования (1), мы называли взаимно симметричными относительно окружности С. Геометрическое построение точки W по данной точке z (или обратно) было указано в гл. I, § 2, п. 5. Следует заметить, что отображение (I) может быть записано в виде:

оно не будет, следовательно, аналитическим преобразованием и принадлежит к классу конформных отображений II рода (гл. II, § 5, п. 4) i При таком отображении углы хотя и сохраняются по абсолютной величине, но имеют разные направления.

Преобразование (II) можно записать в виде: w=w. Очевидно" это преобразование также есть конформное II рода, переводящее каждую точку в точку, ей симметричную относительно действительной оси. Совокупность двух неаналитических (конформных II рода) отображений (I) и (II) даёт аналитическое (при z ф 0) отображение.

w= —. Это отображение будет сохранять углы во всех точках плоскости г, включая z = 0 и г=оо, если под углом двух линий при 2=00 мы будем понимать угол, образованный отображёнными линиями посредством функции w = ~ в плоскости w при w = 0.