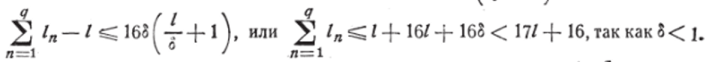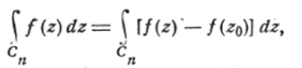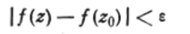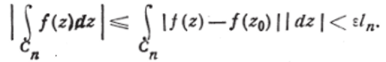Пользуясь последним результатом, возможно придать теореме Коши следующую форму:
Если f (z) есть функция, аналитическая в области D, внутренней к жордановой спрямляемой кривой С, и, кроме того, f{z) непрерывна в замкнутой области D, то 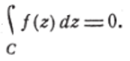
Пусть s — произвольно малое положительное чис^о. Согласно условию /(г) — функция, равномерно непрерывная на D. Следовательно, существует число 8(0 <8< 1) такое, что имеет место неравенство: f (zl) — /(г3)|zh z2 области D, удовлетворяющей условию гх — г2|<23. Согласно следствию 2) леммы п. 7 выбираем число, а и соответственно (J, так что на каждой прямой х=а-]-mb и у= р-J-(/tz = 0, + 1, it2, …) может лежать лишь конечное число точек, общих с кривой С. Прямые jr = aJm3, ^ = р-}-тЗ деляг D, область, внутреннюю к С, на конечное число областей, из которых каждая ограничена жордановой спрямляемой кривой. Обозначим эти кривые Ct Съ Сг. Очевидно, имеем:
где все пути интегрирования проходятся в положительных направлениях. Из кривых Ci, С2, …, Сг пусть первые q, и только они, содержат точки С. Остальные буду г тогда квадраты, расположенные внутри С, и для них.
[f (z)dz = 0 вследствие теоремы Коши (п. 2). Итак,.
d
п
 Ч
Ч
Обозначая через / и 1п длины кривых С и Сл, заметим, что 2 ln — I не л = 1.
превосходит суммы периметров тех квадратов сети, стороны которых содержат точки С. Число этих квадратов не превосходит 4^-^-+0? следовательно,.
Возвращаясь теперь к равенству (II), оценим модуль интеграла f (z)dz:
 Сп
Сп
где го—постоянная точка, выбранная на Сп. Так как диаметр линии Сп не превосходит 8 У 2 <22, то пока г находится на Ся, имеем:
и, значит, 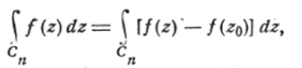
Из равенства (II) после этого получаем:
Так как с — сколь угодно малое положительное число, а 17/ -f 16 — вполне определённое постоянное, то правая часть — произвольно малое положительное число. Левая же часть последнего неравенства есть определённое постоянное число, не отрицательное. Отсюда это число может быть лишь нулём, т. е. 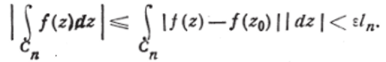
что и нужно было доказать.

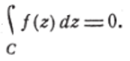
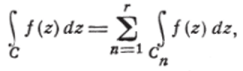
 Ч
Ч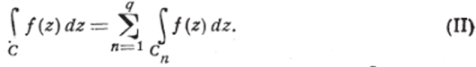
 Сп
Сп