Принцип симметрии Римана-Шварца

Пусть даны две области G, и 0₂, прилегающие друг к другу вЗюль общего куска у их границ, причём область G₂ целиком лежит вне области G_x (фиг. 105). Предположим, что /(z)ecTb функция, голоморфная в области G_t. Если существует функция F (z), голоморфная в области G = G_t -JG₂ -fT" ^co" ставленной из областей G_t, G₂ и точек открытой дуги у" совпадающая с данной функцией f (z) во всех точках области G, то говорят, что функция F (z) является аналитическим продолжением функции f (z) через дугу у. Известно (гл. X, § 1, п. 1), что если такое продолжение функции f (z) возможно, то оно единственное. Основной вопрос, который здесь возникает, состоит в том, чтобы по данной функции / {z) узнать, можно ли её продолжать через некоторый кусок границы области G_t, и если да, то как осуществить это продолжение. Если рассматривавмый кусок у границы области G, представляет дугу некоторой окружности и если значения функции / (z) в точках этой дуги суть действительные числа, то наша функция может быть аналитически продолжена через дугу у. [Под значениями функции f (z) на дуге у мы понимаем непрерывную последовательность предельных её значений изнутри области G_t.j Доказывая это предложение, мы вместе с тем дадим очень простой процесс построения для продолжения данной функции.

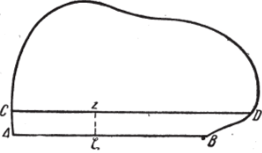
Допустим сначала, что дуга у, через которую мы хотим продолжить функцию /(z), есть часть АВ прямой, параллельной действительной оси (фиг. 106).

Функция /(z) определена с одной стороны от АВ и в точках внутри отрезка АВ, где она принимает действительные значения.

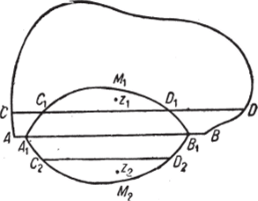
Возьмём лугу А_ХМ₁В₁, лежащую в области G_t, где /(z) определена, и ей симметричную относительно АВ дугу лежащую вне О, (фиг. 107). Определим функцию (р (г) в области, ограниченной замкнутым контуром А₂Мф₁А₂, следующим образом: во всякой точке z₂ этой области, симметричной относительно АВ с точкой z_lt положим:

Эта функция (р (г) будет голоморфной в области, ограниченной контуром А₁М_гВ₁А₁. В самом деле, обозначая через Ь одновременные.

Фиг. 106.

Фиг. 107.

приращения и замечая, что bz₂ и dz_t сопряжены между собой (так как АВ параллельна действительной оси), имеем:

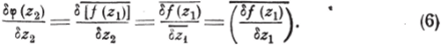
Переходя в равенстве (6) к пределу при Sz, (а значит, и дг₂), стремящемуся к нулю, получим:

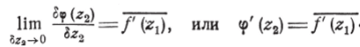
Таким образом, функция <�р (д) имеет конечную производную в каждой точке области, ограниченной контуром А₁М₂В₁А₁, и, следовательно, есть функция, голоморфная в этой области.

Пусть теперь С, Д и С₂?>₂— две хорды, параллельные и симметричные относительно АВ, — расстояние между которыми сколь угодно мало. Обозначая через z' любую точку области, ограниченной замкнутым контуром C_lD_iM_iC_v имеем по формуле Коши:

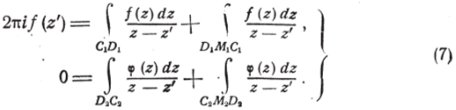
Заставим каждую из хорд C_lD_l и C₂D₂ стремиться к А_ХВ₁. Первый интеграл первого равенства (7) стремится к значению у • В са;

л.в,

мом деле, обозначая через С проекцию на АВ точки z, лежащей на C|Z)_lf имеем:

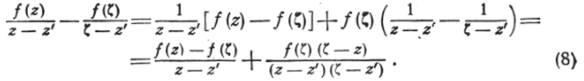
Считая z* постоянной точкой, мы видим, что |z — г'|и |С — z' остаются больше некоторого положительного постоянного числа; с другой стороны, функция f (z) есть ограниченная. Следовательно, модуль выражения (8) может быть сделан как угодно малым; то же самое будет и для его интеграла вдоль CjDj. Таким образом, имеем:

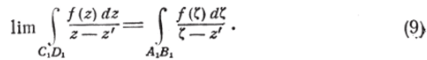
Так же покажем, что будет:

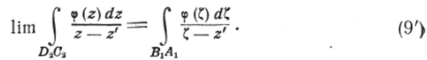
Вспомнив же, что /© имеет действительные значения на АВ, заключаем: /© = <�р© на А_ХВ_Х. Итак, равенства (7) в пределе примут вид.

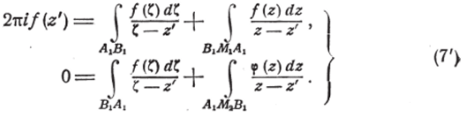
Складывая последние равенства, получим:

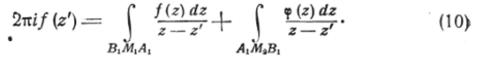
Обозначая через F (z) функцию, определённую на всём контуре Г= B_lM_lA_l—A_lM₂B_l, равную /(г) на дуге А^М^В^ и равную ср (z) на А^М₂В^ перепишем (10) в виде:

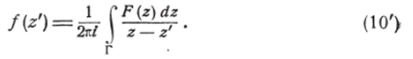
Очевидно, принимая за z' точку области, ограниченной контуром Л₁Ж₂5₁Л_1> мы получили бы: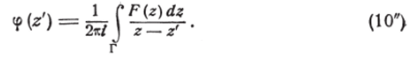

Так как функция, изображаемая интегралом типа Коши.

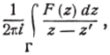
есть голоморфная всюду внутри Г, то из равенства (10') заключаем, что эта функция является аналитическим продолжением через А_ХВ_{ данной функции / (z). С другой стороны, равенство (10″) показывает, что это аналитическое продолжение получается, принимая его значения в точках, симметричных относительно АВ, <�сопряжёнными между собой.

Заметив, наконец, что А_ХВ_Х есть любой отрезок, внутренний к АВ, мы убеждаемся в справедливости принципа.

То же положение может быть обосновано иначе, если воспользоваться вместо ‘интеграла Коши теоремой Морера (гл. IV, § 3, п. 5).

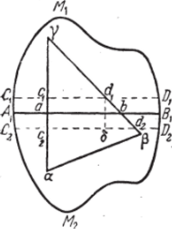
Фиг. 108.

Действительно, обозначив через F (z) функцию, равную /(z) внутри контура А_ХВ_ХМ_ХА₁₉ равную внутри контура A_lM₂B_lA_l9 и, наконец, равную их общему предельному значению в любой точке отрезка A_xB_it мы получим, очевидно, функцию, непрерывную внутри контура A_iM₂B_lM_xA_l. Согласно теореме Морера для доказательства голоморфности функции F (z) достаточно обнаружить, что интеграл от неё, взятый по контуру любого треугольника, лежащего внутри области, где эта функция непрерывна, равен нулю.

Если треугольник afty не пересекается А_ХВ₁₉ то он лежит целиком внутри области, где функция F (z) голоморфна и, следовательно, по теореме Коши, интеграл [ ^mF (z) dz равен нулю. «Зт Если же сфу пересекается Л,?, то, проведя по обе стороны А_ХВ_Х прямые C_XD_X и C₂D₂, параллельные А_ХВ_Х (фиг. 108), получим:

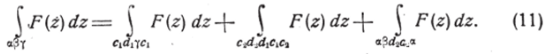
Первый и последний из этих интегралов равны нулю, в силу теоремы Коши; поэтому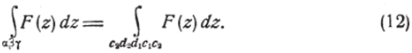

Замечая, что внутри и на контуре сфу модуль F (z) остаётся меньшим некоторого числа /И, и выбирая, далее, прямые C₁D_i и C₂D₂ столь близкими к А_ХВ_Х9 чтобы для любой пары точек С и С|, расположенных, соответственно, по C_xD_t и C₂Z>₂ и притом так, что отрезок CCi параллелен ay, выполнялось бы неравенство: (^(С) — ^(Ci)|s" будем иметь:

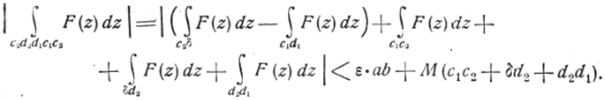
Правая часть неравенства сколь угодно мала, так как г произвольно мало и, кроме того, сумма длин отрезков СуС₂, bd₂ ^и d₂d_v может быть сделана сколь угодно малой, при CyDy и С₂Ц>, достаточно близких к ЛуВ[. Так как, далее, в силу (12), величина.

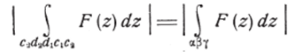
не зависит от положения прямых CyDy и С, Ц>, то она равна нулю, чем и заканчивается доказательство.

Если воспользоваться обобщением теоремы Коши, данным в гл. IV, § 2, п. 8, то последний анализ становится излишним. В самом деле,.

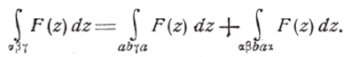
Так как функция F (z), голоморфная внутри каждого контура abya^% и а$Ьаа, остаётся непрерывной на них, то в силу обобщённой теоремы Коши оба интеграла правой части последнего равенства будут нулями, откуда следует: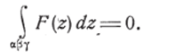

При доказательстве мы существенно предполагали, что прямолинейный отрезок АВ расположен параллельно действительной оси. Остаётся теперь освободиться от этого ограничения. Пусть дуга у, через которую мы хотим продолжить функцию f{z)_y есть какой-нибудь прямолинейный отрезок АВ. Этот случай немедленно приводится к предыдущему, если выполним вращение: z'= ze^hi, посредством которого отрезок АВ становится параллельным действительной оси. Ясно, что значения аналитического продолжения функции f (z) будут сопряжёнными в точках, симметричных относительно отрезка АВ.

Наконец, если у есть дуга некоторой окружности, то этот случай сводится на только что рассмотренный, если выполним линейное пре;

образование z =—, посредством которого дуга у преобразуется в прямолинейный отрезок АВ. Известно (гл. Ill, § 1, п. 7), что при таком преобразовании паре точек z_y симметричных относительно дуги окружности у, будет соответствовать пара точек, симметричных относительно прямолинейного отрезка АВ. Следовательно, значения аналитического продолжения функции f (z) в точках, симметричных относительно у, будут сопряжёнными между со’ой.

Итак, мы ожем формулировать принцип симметрии в таком виде: функция f (z), голоморфная в области G, граница которой содержит дугу окружности у (или прямолинейный отрезок у), принимающая во всех точках внутри у непрерывные (изнутри G_t) действительные значения, аналитически продолжается через у. Значения этого аналитического продолжения функции f (z) вне области G_t будут сопряжёнными с f (z) в точках, симметричных относительно у.

Этот принцип имеет многочисленные приложения в теории конформных отображений. Действительно, пусть дана область G_t, граница которой содержит дугу окружности у (^в частности, прямолинейный отрезок у), такая, что область G₂, симметричная с G_t относительно у, целиком лежит вне G_{. Если функция w = f (z) даёт конформное отображение области G_{ на верхнюю полуплоскость, то мы получаем согласно принципу симметрии аналитическое продолжение через у функции /(z), приписывая ему взаимно сопряжённые значения в двух точках, являющихся взаимно симметричными относительно у. Следовательно, функция w = f (z), будучи продолжена через у, даёт конформное отображение области G = G, -fG₂ + у, составленной из областей G_t, G₂ и точек открытой дуги у, на плоскость w, из которой выкинуты точки действительной оси, за исключением тех точек, которые лежат внутри отрезка, явчяющегося отображением дуги у. Легко видеть, как обобщается формулировка принципа РиманаШварца, если функция w = f (z) даёт конформное отображение на круг.

В приведённой выше формулировке принципа симметрии значения, принимаемые f (z) на дуге окружности у, располагались на отрезке действительной оси. Легко обобщить этот принцип на случай, копа значения, принимаемые /(.г), сами располагаются на дуге некоторой окружности С. В самом деле, выполняя над w = f (z) линейное преобразование, переводящее С в действительную ось, мы сведём этот случай к разобранному выше. Так как при этом линейном преобразовании точкам, симметричным относительно действительной оси, будут отвечать точки, симметричные относительно окружности С, то можно утверждать, что точкам г, симметричным относительно у, отвечают значения f (z), симметричные относительно С.