Факторы накопления гетерогенных сред

ФН зависит также от того, является среда гомогенной или гетерогенной (состоящей из различных материалов). Мы рассмотрим лишь среду, состоящую из плоских слоев. В этом случае ФН дополнительно зависит от числа слоев, материала слоев, их толщины и взаимного расположения. Очевидно, что практически невозможно табулировать ФН для такого количества переменных (вспомним, что еще ФН зависит от энергии источника и его углового распределения). Для каждого конкретного случая ФН можно рассчитать численно (например, методом Монте-Карло) или измерить экспериментально. На основе этих данных можно получить эмпирические формулы, которые полезны при решении различных практических задач.

Рассмотрим два выражения для оценки ФН гетерогенной защиты, состоящей из /V слоев с толщиной i-слоя I-с/^ в ДСП. Их можно использовать для точечных и плоских источников в барьерной геометрии [8].

1) ФН гетерогенной среды равен ФН материала последнего слоя для полной оптической толщины защиты.

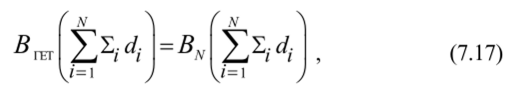
где /V-слой — самый удаленный от источника. Формула (7.17) дает неплохие результаты, если толщина последнего слоя Е_л, d_N > 3.

2) Формула Бродера с сотр. Широко используется для инженерных расчетов ФН гетерогенных сред.

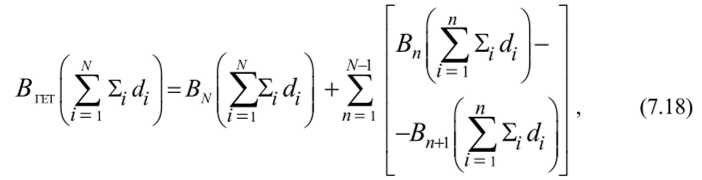
где B_lET — ФН гетерогенной среды, В_п — ФН гомогенной среды из материала /7-слоя на соответствующей толщине защиты.

Если гетерогенный поглотитель состоит из двух слоев с различными материалами (1 и 2), го в соответствии с формулой (7.18) имеем.

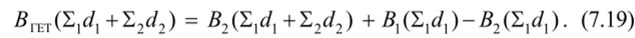
На рис. 7.3 показана графически схема расчета ФН в соответствии с выражениями (7.18) и (7.19) для двухслойного поглотителя, состоящего из слоев алюминия и железа.

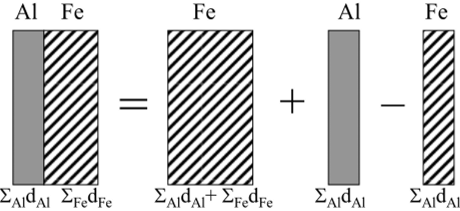
Рис. 7.3. Схема расчета ФН для поглотителя из двух слоев по формуле (7.19)

Формула (7.18) дает хорошие результаты при переходе из среды с большим Z в среду с меньшим Z и не воспроизводит истинной зависимости ФН от толщины в противном случае, когда тяжелая среда следует за более легкой. Причиной этого является неучет переходных эффектов — изменения плотности потока прямого и отраженного излучения вблизи фаниц слоев из разных веществ. Переходные эффекты являются следствием изменения коэффициентов взаимодействия излучения при переходе из одной среды в другую.

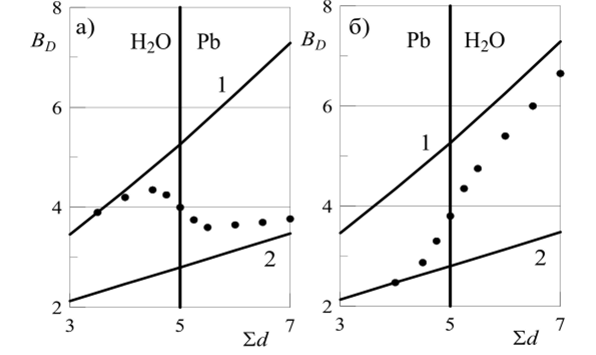
Рис. 7.4. Зависимость дозового ФН плоского мононаправленного источника фотонов с энергией 2 МэВ от толщины гетерогенной защиты (бесконечная геометрия). Сплошные кривые: I — вода: 2 — свинец. Точки — в гетерогенной среде.

Основные закономерности поведения ФН в гетерогенных средах видны из рисунков 7.4 и 7.5. На рис. 7.4 показана зависимость ФН в двух гетерогенных средах: вода-свинец и свинец-вода. Расчет ФН выполнен в бесконечной геометрии, когда детектор находится внутри поглотителя. В этой геометрии изменение ФН слева от границы раздела сред обусловлено в основном изменением обратного потока фотонов. Если Z второго вещества больше, чем у первого, то обратный поток уменьшается (см. рис. 7.4, а). Если же Z второго вещества меньше, чем у первого, то обратный поток фотонов возрастает (см. рис. 7.4, б).

На рис. 7.5 показана зависимость ФН для тех же гетерогенных сред, но уже в барьерной геометрии, когда детектор находится па правой границе барьера (в воздухе) и обратный поток от границы барьера отсутствует. Из рис. 7.5 следует, что для барьерной геометрии поведение ФН в гетерогенной среде обусловлено практически лишь изменением прямого потока излучения.

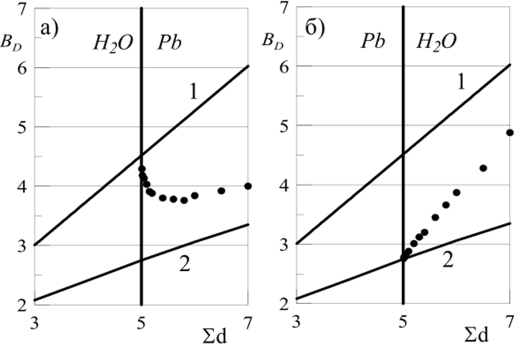
Рис. 7.5. Зависимость дозового ФН плоского мопонаправленного источника фотонов с энергией 2 МэВ от толщины гетерогенной защиты (барьерная геометрия). Сплошные кривые: 1 — вода; 2 — свинец. Точки — во втором слое гетерогенной среды.

Расчеты для обеих геометрий выполнены методом Монте-Карло по программе «Компьютерная лаборатория» (см. приложение 1).

В работах [5, 8, 10] приведены и анализируются другие, более точные, формулы для расчета ФН гетерогенных сред. Но более точные выражения, как правило, используют дополнительные параметры, значения которых имеются в литературе лишь для ограниченного набора геометрий.