Схемы включения преобразователей

С помощью схемы включения (СВ) выходной сигнал первичного ИПр преобразуется в электрический сигнал, удобный для его последующей обработки, передачи или хранения. Выбор схемы включения зависит от типа ИПр и требований к выходному сигналу. В зависимости от типа ИПр различают СВ для генераторных и параметрических ИПр, в зависимости от требований к выходному сигналу — схемы включения с амплитудно-модулированным выходным сигналом (АСВ) и схемы включения с частотно-модулированным выходным сигналом (ЧСВ).

Схемы включения с выходным АМ-сигналом

Электрические генераторные ИПр создают на своем выходе напряжение и_х, ток i_x или заряд q_x, зависящие от измеряемой величины х. Основным элементом схем включения таких ИПр является усилитель электрического сигнала [21J. В настоящее время широкое применение получили операционные усилители (ОУ). Они выполняются по интегральной технологии, имеют стабильные характеристики и могут использоваться не только для усиления (масштабирования) сигналов, но и большого числа других преобразований: дифференцирования, интегрирования, сравнения и пр. Поэтому области применения ОУ интенсивно расширяются.

При использовании параметрических ИПр измеряемая величина преобразуется в изменение собственного параметра преобразователя. Обычно таким параметром являются активное сопротивление R_v емкость С_х или индуктивность L_x преобразователя, зависящие отх. Соответствующие ИПр называются омическими, емкостными или индуктивными.

Наиболее распространенными схемами включения параметрических ИПр являются схема делителя напряжения (рис. 2.10, а) и мостовая схема (рис. 2.10, 6). Обе схемы являются схемами с амплитудно-модулированным выходным сигналом.

Делитель напряжения образован двумя последовательно соединенными резисторами R_{ и R₂ (рис. 2.10, а). Омический ИПр можно использовать в качестве резистора R_{1 в качестве резистора R₂ или (если ИПр дифференциальный) в качестве обоих резисторов. Источник электрического питания И создает на своих зажимах cd ЭДС U_n. Внутренним сопротивлением источника R_n обычно пренебрегают. Это возможно, если мощность источника питания значительно превышает мощность, потребляемую делителем и указателем. Указатель У к, имеющий сопротивление R_}V служит для регистрации выходного напряжения U_x или силы тока /_г, зависящих от измеряемой величины.

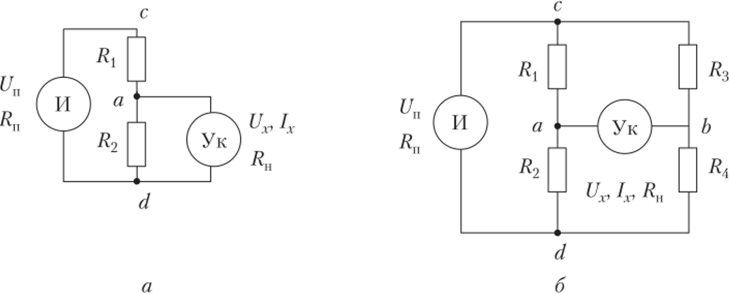
Рис. 2.10. Схемы включения параметрических ИПр:

а — делитель напряжения; б — мост Уитстона Напряжение питания делителя U_n может быть переменным. В этом случае в качестве резисторов и (или) R₂ можно использовать емкостный и (или) индуктивный ИПр, а в качестве указателя — фазочувствительный выпрямитель (демодулятор).

Зависимость выходного напряжения делителя U_x от сопротивлений R_{ и R₂ имеет вид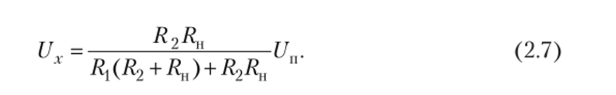

Если R_}{ ^>R₂, то делитель работает в режиме холостого хода. В этом случае вместо (2.7) нужно записать.

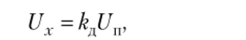
где k_;i = R₂/(R + /?₂) ^— коэффициент передачи делителя (0 < k_;i < 1).

Делитель и источник питания образуют ИУ, с помощью которого измеряемая величина х преобразуется в напряжение U_x. Зависимость относительного изменения этого напряжения.

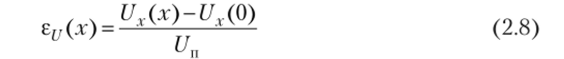
от измеряемой физической величины х определяет статическую характеристику ИУ.

Обычно ИПр, входящий в схему делителя, имеет линейную статическую характеристику вида где R₀ — начальное сопротивление ИПр; а_х — относительный коэффициент чувствительности ИПр к измеряемой физической величине х. В этом случае статическая характеристика ИУ (2.8) имеет вид

где значения коэффициентов а, b зависят от состава элементов и параметров делителя: если R₁ = R_x, то если R₂ = R_x, то.

R_n

где р — относительное сопротивление пассивного плеча делителя; а = ——.

относительное сопротивление нагрузки.

Обычно 0 < х < х_в или |х| < х_в, где х_в — верхний предел диапазона измерений. В этих случаях произведение г# = oc_vx_B определяет максимальное значение относительного изменения сопротивления ИПр. Оно может изменяться в широких пределах — от 10^-5 (для тензорезистивных ИПр) до 1 (для реостатных ИПр).

Максимальная приведенная погрешность от нелинейности статической характеристики ИУ (2.10) зависит только от безразмерного параметра q — Ьх_в и вычисляется по формулам п. 2 табл. 2.3. С ростом q погрешность у_п увеличивается.

Таблица 23

Погрешность от нелинейности статических характеристик

мостовых ИУ

Чувствительность ИУ максимальна, если делитель работает в режиме холостого хода и является равноплечим. В этом случае AU_x/U_n = 0,25ед, т. е., если изменение сопротивления одного из плеч делителя равно, например, 4%, то изменение выходного напряжения ИУ ДU_x не превышает 1% от напряжения питания U_n.

При случайных изменениях параметров делителя возникают инструментальные погрешности ИУ. Их максимальное значение можно оценить по формуле.

AU_{U R} A a Afe.

где ot/_n =-or/ = —, 00 = ——максимальные относительные измене;

U_n a b

ния параметров [/", 0, ft. Если отклонения этих параметров вызваны одной причиной (например, изменением температуры окружающей среды), то при расчете инструментальной (соответственно, температурной) погрешности у, нужно учитывать знаки слагаемых. С ростом параметра q погрешность у_н уменьшается.

В делителе рис. 2.10, а можно использовать дифференциальный ИПр (например, реостат со средней точкой) или два дифференциально включенных ИПр (например, два тензорезистора). В этом случае.

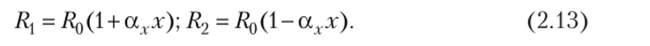
Статическая характеристика ИУ с таким ИПр имеет вид.

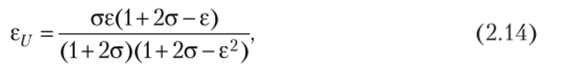
где г = а_хх, |е| < 1. Условие у_п 30 [30].

Разновидностью делителей напряжения, работающих на переменном токе, является резонансная схема включения [31]. В этом случае делитель содержит резонансный контур, в который включается ИПр. Параметры контура подбирают так, чтобы рабочий участок статической характеристики И У располагался на склоне амплитудно-частотной характеристики контура. При высокой добротности контура достигается большая чувствительность ИУ.

Основным недостатком делителя напряжения является то, что при х = 0 его выходное напряжение (или амплитуда этого напряжения) не равно нулю. Для устранения этого недостатка применяют мостовую схему включения. В качестве такой схемы обычно используют мост Уитстона. В этом случае к делителю R_t, R₂ добавляется еще один делитель /?₃, /?₄ (см. рис. 2.10, б) так, чтобы напряжение U_x на указателе У к или ток 1_Х> протекающий через него, в случае х = 0 отсутствовали. Это условие выполняется, если при х = 0 соблюдается равенство.

называемое условием равновесия моста.

Участки ас, ad, be и bd мостовой схемы называются плечами моста. Если плечо содержит ИПр, то такое плечо называется активным, если нет — то пассивным. Участок cd называется диагональю питания моста, а участок ab — измерительной диагональю.

Условие (2.15) может выполняться при разных соотношениях сопротивлений плеч моста. На практике применяют симметричные мосты. Такими мостами являются: равноплечий мост (РИМ), у которого при х = 0 сопротивления всех плеч моста равны друг другу, т. е. R^= R₂ = R₃ = R_A = R₀, последовательно-симметричный мост (ПОСМ), у которого при х = 0 выполняются равенства R_] = R₂ = R^, R₃= R_A= г и параллельно-симметричный

мост (ПРСМ), у которого при х = О выполняются равенства /?, = R₃ = R$y R₂ = R_a= г (табл. 2.4, 2.5).

Схема равноплечего моста с одним ИПр (РПМ1) применяется редко из-за существенной нелинейности статической характеристики и больших инструментальных погрешностей. Эти недостатки отсутствуют при использовании схем с дифференциальными преобразователями (ПОСМ и ПРСМ). Параллельно-симметричная схема отличается от последовательно-симметричной тем, что в ней допускается использование низкоомных ИПр, у которых Ло «:г. Применение таких ИПр в схеме ПОСМ приводит к шунтированию источника питания. Схема РПМ4 содержит четыре дифференциально включенных ИПр и обеспечивает наибольшую чувствительность ИУ.

Таблица 2.4

Типы мостовых схем

Для сопротивлений пассивных плеч моста г и сопротивления нагрузки R_u принимается соответственно г = и R_n = о/^, где р, о — постоянные положительные числа. Случай р = 1 соответствует равноплечему мосту, случай ст:"1 — работе моста в режиме холостого хода, случай, а = 0 — работе моста в режиме короткого замыкания, случай р = р_с, а = а_с — выделению максимальной мощности сигнала Р_х = I%R_n в измерительной диагонали моста.

В табл. 2.5 приведены такие значения параметров р и а. Условиями экстремума мощности для моста типа ПОСМ являются равенства р_с =0 и р_с = °о. Точное выполнение этих равенств невозможно из-за ограничений, наложенных на мощность источника питания моста и тепловую мощность рассеяния ИПр. Поэтому значения параметров р_с = а_с. = 1 для этого моста, указанные в табл. 2.5, являются условными.

Таблица 25

Согласованные параметры мостовых схем

Ток в измерительной диагонали моста пропорционален напряжению источника питания U_n и зависит от сопротивлений плеч моста.

где.

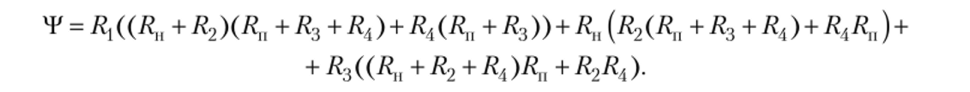
Степень неравновесия моста можно оценивать величиной М = R_XR₄ — - R₂R^ Для уравновешенного моста М = 0.

Обычно внутренним сопротивлением источника питания пренебрегают, полагая R_u —> 0. В этом случае вместо (2.16) можно записать.

Если мост питается от источника тока, то, напротив, R_u —"°° В этом случае.

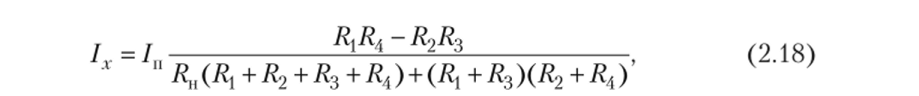
где 1_П — ток питания моста. Во всех случаях напряжение U_x в измерительной диагонали моста равно.

Если относительные изменения сопротивлений плеч моста е, = (/?, — - R₀)/R₀ незначительные (т.е. если «:1), то в первом (линейном) приближении можно записать.

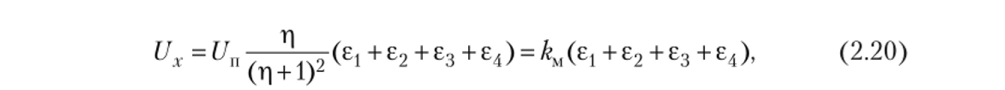
R о R" ± о м 1 1 м где Г| = —— = —— — постоянный коэффициент, характеризующий асим;

^20 ^40.

метрик) плеч моста; R_i0 — номинальное значение /-го сопротивления; ki =?/_пЛ/(г1 + 1)^2 — чувствительность моста. В этом случае мостовую измерительную схему можно рассматривать в качестве суммирующего или сравнивающего элементов.

Чувствительность моста k_M зависит только от величины напряжения питания U_n и соотношения сопротивлений плеч моста (коэффициента л) — Чувствительность равноплечего моста (у которого л = 1) максимальна. Отклонения коэффициента л от оптимального значения л = 1 в полтора-два раза несущественны. На границах интервала 0,665 снижение чувствительности не превышает 4% от максимального значения &_мтах = 0,25U_n. Резкое снижение чувствительности происходит только при л^0,4. Выбор напряжения питания U_n зависит от необходимой величины выходного сигнала U_x и допустимой мощности рассеяния используемых ИПр.

Мостовая СВ и ИПр образуют мостовое И У, с помощью которого измеряемая физическая величина х преобразуется в изменение напряжения постоянного тока U_х или тока 1_Х.

В зависимости от режима работы моста и вида источника питания статическая характеристика такого ИУ описывается одной из четырех функций 1301.

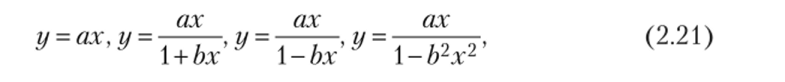
где у — напряжение или ток в измерительной диагонали моста; а, b — постоянные коэффициенты, зависящие от параметров мостового ИУ. На рис. 2.11 показаны графики этих функций.

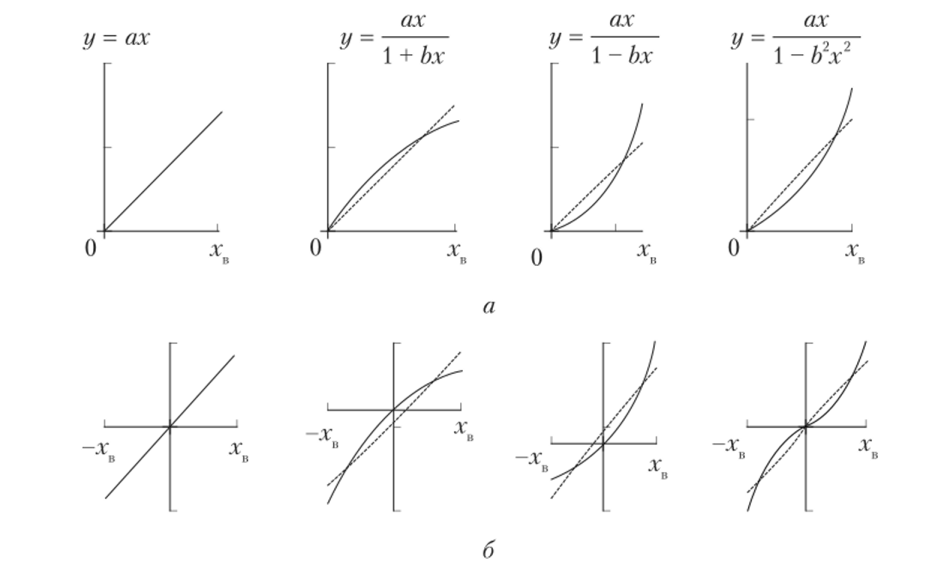
Рис. 2.11. Статические характеристики мостовых ИУ:

а — для случая 0<�х<�х_в; 6 — для случая -х_в <�х<�х_а

Пунктиром показаны аппроксимирующие прямые уА + Вх (прямые наименьших модулей). При правильном выборе их параметров максимальная приведенная погрешность от нелинейности статической характеристики ИУ у_п является минимальной. Эта погрешность зависит только от произведения q = bx_B и вычисляется по формулам, приведенным в табл. 2.3. Расчеты по этим формулам показывают, что погрешность от нелинейности статических характеристик мостовых ИУ с одиночными ИПр значительно превышает погрешность от нелинейности статических характеристик И У с дифференциальными ИПр [30].

В табл. 2.6 приведены схемы мостовых ИУ, их статические характеристики и формулы, связывающие значения коэффициентов а, b этих характеристик с параметрами ИУ для случая, когда мост работает в режиме заданного напряжения (питается от источника напряжения).

Статические характеристики мостовых ИУ

Считается, что во всех случаях используемые ИПр имеют линейные статические характеристики (2.13), а информативным параметром выходного сигнала является напряжение U_x в измерительной диагонали моста.

Если известны желаемое значение коэффициента наклона аппроксимирующей прямой В (т.е. желаемое значение средней чувствительности схемы включения) и допустимая погрешность от нелинейности статической характеристики И У (2.21) у_д, то необходимые значения коэффициентов а_у b этой характеристики можно вычислить по формулам, приведенным в табл. 2.7.

С их помощью можно выбрать тип моста и определить его параметры, обеспечивающие получение желаемой статической характеристики мостового ИУ. При этом должны приниматься во внимание конструктивные, технологические и иные ограничения [30].

Максимальную чувствительность и линейную статическую характеристику имеет мост РПМ4, работающий в режиме холостого хода. Также линейными являются характеристики мостов ПРСМ и Р11М4, работающих в режиме заданного тока.

В ряде случаев не сопротивление R_x, а проводимость ИПр Y_x =1 /R_x линейно связана с измеряемой величиной, т. е.

Оптимальные значения параметров статических характеристик мостовых ИУ.

В этих случаях линейную статическую характеристику имеют мосты ПОСМ и РПМ4, работающие в режиме заданного напряжения [30].

При отклонении параметров мостовых ИУ от номинальных значений появляется инструментальная погрешность, которая обычно связана с изменением температуры окружающей среды. В этом случае вместо (2.9) следует записать.

где Rq_T> а_хТ — начальное сопротивление и коэффициент относительной чувствительности ИПр, вычисленные с учетом фактического значения температуры окружающей среды Т. В первом (линейном) приближении их можно вычислить по формулам.

где a_Ry — температурные коэффициенты величин Rq и а.

X'.

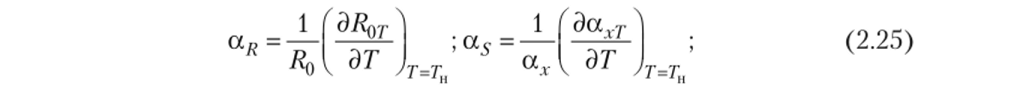
АТ = Т-Т_и — отклонение температуры Т от нормальной температуры Т_н = 20 °C. Окончательно при АТ Ф 0 вместо (2.9) получаем.

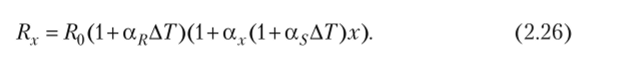
Подставляя (2.26) в формулы (2.16)—(2.19), можно для каждого из рассматриваемых мостовых ИУ найти абсолютную температурную погрешность.

где U_xT — выходное напряжение моста, вычисленное с учетом фактического значения температуры окружающей среды; U_х — то же для нормальной температуры окружающей среды.

Приведем результаты такого анализа [30]. Температурная погрешность РПМ1, работающего в режиме заданного напряжения, практически не зависит от текущего значения измеряемой величины х и в первом приближении вычисляется по формуле.

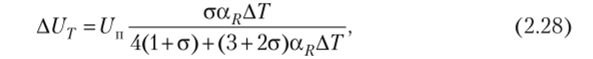
т.е. является аддитивной погрешностью. Температурная погрешность мостов с дифференциальными ИПр (ПОСМ, ПРСМ и РПМ4) является мультипликативной (пропорциональной х). Для мостов ПОСМ и РПМ4 ее можно вычислить по формуле.

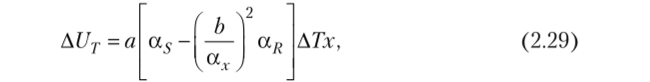
где значения коэффициентов а, b берутся из табл. 2.4. Например, абсолютная температурная погрешность моста РПМ4 вычисляется по формуле.

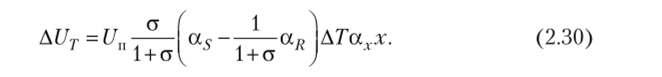
Для моста ПРСМ вместо (2.29) нужно записать.

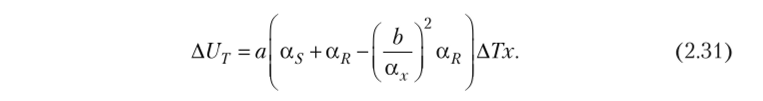
Максимальная приведенная температурная погрешность рассматриваемых мостов равна.

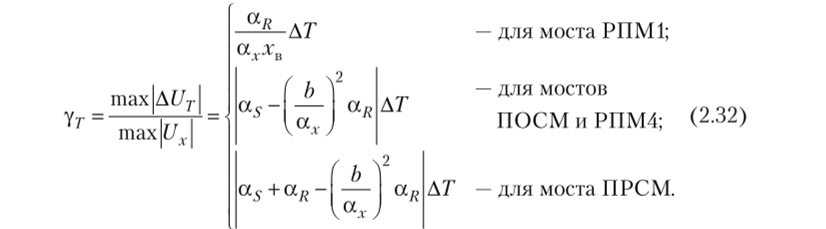
Температурная погрешность моста РПМ1 более чем на порядок превышает температурную погрешность мостов, имеющих дифференциальные преобразователи. Условием компенсации температурной погрешности являются равенства.

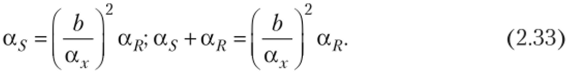
Другим способом уменьшения мультипликативной температурной погрешности мостовых И У является подключение в цепь источника питания компенсационного резистора R_T, величина которого зависит от температуры окружающей среды. В этом случае температурное изменение чувствительности ИУ парируется изменением напряжения питания моста U_n.

При производственно-технологических отклонениях параметров мостовых И У также появляются инструментальные погрешности, зависящие от номинального значения сопротивления ИПр R₀. Для их уменьшения используются различные регулировки, способствующие выполнению условия (2.15), включение в схему моста калибровочных резисторов и пр. С помощью мостов Уитстона, работающих в нормальных условиях, приемлемые результаты получаются в диапазоне R₀ от 100 Ом до 100 кОм [15]. Для преобразования малых сопротивлений (до 10 Ом) применяют двойные (шестиилечие) и другие мосты: Т-образные, мосты Баттерворта, Андерсона, Ремингтона и др.

Для емкостных и индуктивных ИПр, имеющих реактивное сопротивление, применяют мосты переменного тока. В этом случае в качестве вторичного прибора используют фазочувствительные указатели [31].

Для устранения нелинейности статической характеристики мостовой схемы применяют самобалансирующиеся мосты, называемые также мостовыми усилителями (рис. 2.12) [21]. В них используются операционные усилители (ОУ) с глубокой отрицательной обратной связью.

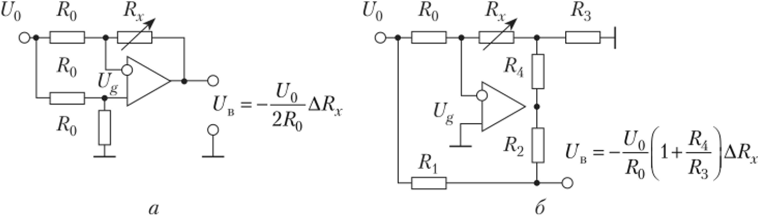
Рис. 2.12. Мостовые ИУ с линейной статической характеристикой:

а — без усиления сигнала; 6 — с усилением сигнала В схеме рис. 2.12, а для ОУ, включенного в измерительную диагональ моста, выполняется условие квазинуля (U_g —> 0). В этом случае выходное напряжение ОУ пропорционально относительному изменению сопротивления ИПр e_R = AR_x/R₀. В схеме на рис. 2.12, б достигается дополнительное усиление сигнала по напряжению за счет установки в цепь отрицательной обратной связи ОУ Т-образного эквивалента большого сопротивления.