Закон сохранения механической энергии

Пусть на частицы 1, 2 системы действуют внутренние консервативные силы f₁₂ = -f_2I и внешние силы F, F₂. Их работа приводит к приращению кинетической энергии частиц: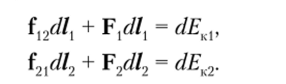

Складывая эти равенства почленно, получим.

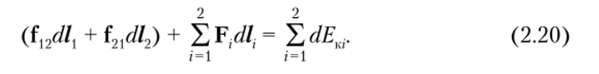
В скобках — работа консервативных сил системы, которая в соответствии с формулой (2.10) равна убыли ее потенциальной энергии. Второй член — работа 5Л_ВМ внешних сил, а правая часть (2.20) — это приращение кинетической энергии системы:

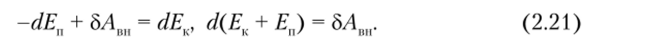
Если частиц больше, то больше исходных равенств, но результат тот же. Итак, если между частицами системы действуют только консервативные силы, то приращение ее полной механической энергии равно работе внешних сил.

Этот закон регулирует поведение множества систем, например течение жидкости. Если не учитывать трение, то между сечениями 5, и S₂ трубы она движется под действием результирующей силы F, + F₂ (рис. 2.9). В границах S[, S₂ ее энергия не изменяется, а изменение энергии ее порции Ат определяется работой внешних сил F, и F₂ на границах участка.

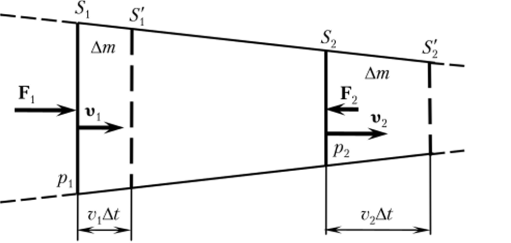
Рис. 2.9.

На основании формулы (2.21) при dE_n = 0 (труба горизонтальная) имеем.

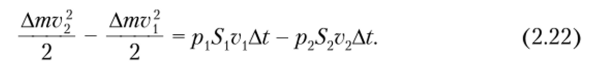
Здесь учтено, что At мало, и потому на расстояниях v_{At и v₂At давление и сечение трубы практически постоянны.

При стационарном течении масса Ат жидкости, протекающей через сечение Sj за время At, равна массе жидкости, протекающей за то же время через сечение S₂ (см. рис. 2.9):

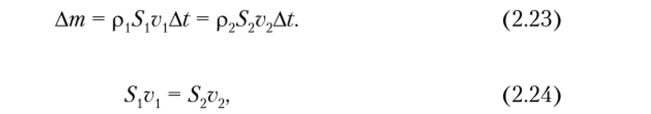
Отсюда поскольку для несжимаемой жидкости p_t = р₂ = р. Равенство (2.24) называется уравнением непрерывности струи.

Подставляя соотношения (2.23) и (2.24) в формулу (2.22), получим уравнение Бернулли.

Оно относится не только ко всему сечению трубы, но и к любой трубке тока в объеме текущей жидкости. Под ней понимают объем, ограниченный линиями тока, касательные к которым совпадают с направлениями скоростей частиц жидкости.

Уравнение (2.25) показывает, что в сечениях потока с повышенной скоростью давление надает. Как следует из равенства (2.24), это происходит, например, в сужениях трубы.

Уравнение Бернулли имеет множество технических применений (пульверизация, сопла турбин, конструкции летательных аппаратов и т. д.). На рис. 2.10 показано сечение крыла самолета, разветвляющего струю воздуха. По его выпуклой части он за то же время проходит больший путь, т. е. имеет большую скорость, что соответствует меньшему давлению. Разность давлений и вызывает подъемную силу.

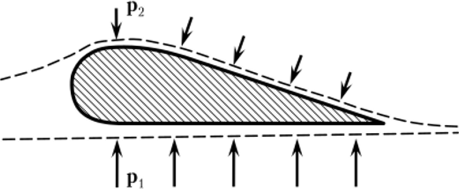
Рис. 2.10.

Если система частиц замкнута, то в уравнении (2.21) 8Л_ВП = 0, d (E_K + Е_п) = 0 и, следовательно,.

т.е. если между частицами замкнутой системы действуют только консервативные силы, то ее полная механическая энергия остается постоянной.

Именно этот закон и отражает универсальность понятия «энергия» для разных форм движения материи. В данном, частном, случае он называется законом сохранения механической энергии (одним из его первооткрывателей был Дж. Джоуль).

Примеры практики Для того чтобы ракета освободилась от тяготения Земли, се стартовая кинетическая энергия должна быть не меньше приращения потенциальной энергии ракеты при удалении с поверхности Земли на бесконечность:

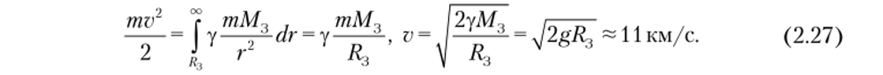
Это значение называется второй космической скоростью. Им руководствуются при проектировании межпланетных перелетов.

При бросании различных снарядов их начальная кинетическая энергия преобразуется в потенциальную, а затем происходит обратное преобразование. Пружина затвора стрелкового оружия осуществляет преобразование энергии упругой деформации в кинетическую энергию бойка: kx?/2 = mv²/2. Как следует из этой формулы, получаемая кинетическая энергия пропорциональна упругой силе и абсолютной деформации. Именно поэтому в древности перешли от лука к арбалету. Упругая сила и натяжение лука определяются ограниченными физическими возможностями человека, а для натяжения упругих элементов арбалета применяют дополнительные приспособления — рычаги, вороты и т.н.

Подчеркнем, что в формулах (2.21), (2.26) нс учтены силы трения. Будучи неконсервативными, они нарушают сохранение механической энергии, поскольку часть ее переходит в теплоту, однако сумма тепловой и механической энергий дает ту же константу. Какие бы формы энергии ни присутствовали в системе, их сумма неизменна.

Энергия не уничтожается и не создается, а только перераспределяется между элементами материи, переходя из одной формы в другую.

Закон сохранения энергии как бы «сшивает» их друг с другом.