Условие Вейерштраеса в пространственной задаче

Перейдем к процедуре построения неравенства Вейерштраеса сильного экстремума. Как мы уже видели, построение неравенства Вейерштраеса сильного экстремума как в простейшей задаче, так и в пространственных вариационных задачах представляет собой отдельную проблему, связанную с характером выбора малой области, в которой проводим варьирование функции. Этот вопрос рассматривался К. А. Лурье [7], который показал, что от вида области варьирования зависит сам характер неравенства Вейерштрасса — в том смысле, что оно получается более или менее «сильным». Например, выбрав за такую область круг, получаем один вид условий, выбрав вытянутый эллипс, — другой, причем во втором случае эти условия получаются в определенном смысле более сильными, чем в первом случае.

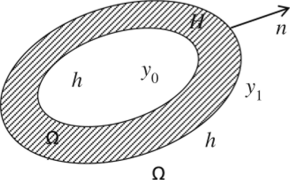
Рис. 7.4. К построению неравенства Вейерштраеса.

В нашей задаче за область варьирования мы выберем кольцевую область, изображенную на рис. 7.4. Полагаем при этом, что сама эта область образована двумя гладкими кривыми у₀ и у, векторные уравнения которых соответственно a (s) и b (s), причем a (s) =h (s)+e (p (s), (7.45).

где cp (s) — уравнение произвольной гладкой кривой; е — малый векторный параметр.

Рассмотрим приращение функционала за счет приращения функции h (x, у) на постоянную величину Н внутри Q' и подвижности у, у₀:

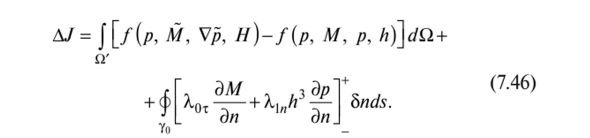
В формуле (7.46) выражение в квадратных скобках в первом интеграле есть полное приращение функционала за счет приращения Н внутри Q', которому отвечают соответствующие приращения функций М и Vp. Но структура подынтегральной функции исходного функционала (7.35) такова, что f{p, М, Vp, H)-f (p, М, Vp, h) = 0, так как все уравнения-ограничения выполняются в Q'. Заметим, что в согласии с (7.45) Ьп = |с| ф. Таким образом, значение полного приращения ДJ определяется контурным интегралом:

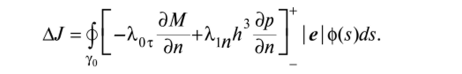
Будем уменьшать малый параметр е, что отвечает предельному переходу для сильных вариаций И в малой области, и, вспоминая рассмотренную в п. 1.3 формулу для приращения функционала, рассмотрим величину.

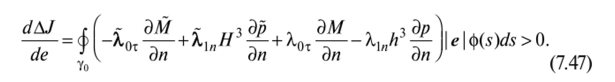
Заметим, что в согласии с первыми двумя условиями Эрдманна-Вейерштрасса (7.42) Х,_0т. = ?1_0т и X.,"Я³ = Х,_|яЛ³, т. е. подынтегральная функция принимает вид:

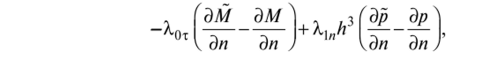
и так как ф (х) — любая гладкая функция, то при е~> 0 имеем в согласии с (7.47) поточечно в Q:

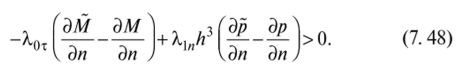
Приведем неравенство (7.48) к более удобному виду, исключив ЭЛ/ др

из него разрывные на у_п величины —— и — и вспоминая, что Эя Эя.

Q = rot (Mk):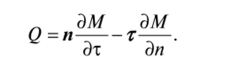

Таким образом, Q_n =—— — нормальная компонента расхода и Эт.

_ дМ

она непрерывна, тогда как касательная компонента Q_x = —-—.

Эя разрывна. Причем в согласии с (7.32) имеем для этих компонент такие выражения:

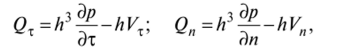
др.

где величина — непрерывна по непрерывности давления, тогда Эт как — может быть разрывна.

Эт Теперь рассмотрим значения разностей производных в (7.48): 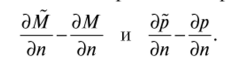Для первой из этих разностей.

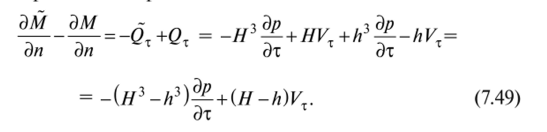
Аналогично, для по непрерывности величины О, (спра;

Эя Эя ва и слева от линии разрыва функции И)

откуда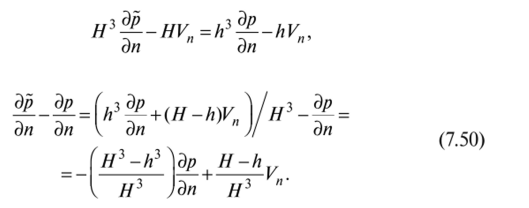

Подставляя (7. 49) и (7. 50) в (7.48), получим.

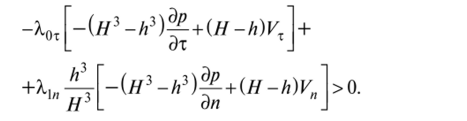
d — ЭЛ. _ ЭЛ.

Вновь вспоминая, что Л._0х =—, л._1п =—, перепишем неравенство в виде.

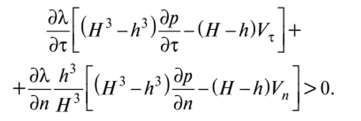
Добавляя и вычитая отсюда величину найдем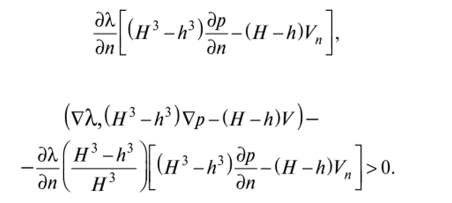

После простых преобразований получаем следующее выражение для неравенства Вейерштрасса:

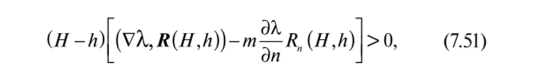
где вектор R и параметр т имеют вид:

R (H, h)=(H² + Hh+h²)Vp-V-, т ={Н²-И²)/Н (7.52).

При этом вектор — функция R, определенная на всех допустимых значениях Я, удовлетворяющих ограничению (7.34); R_n — нормальная компонента вектора R, причем функциир и X в (7.51) вычисляются на оптимальном профиле И, а нормаль рассматривается как внешняя по отношению к границе «области варьирования».

Согласно (7.34) интересны два варианта значений управляющей функции профиля А, а именно A = A_mjn = 1 и A > 1.

В первом случае в (7.34) Я—A_min > 0, тогда как во втором, в промежуточном режиме, Я—А знакопеременно. Но во втором случае в силу двух последних уравнений (7.37), из которых, в частности, следует Х₂ = 0: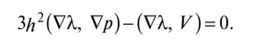

Отсюда получаем, что в промежуточном режиме.

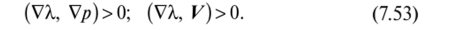
При A = h_min величина Я — h_min > 0, и знаки соответствующих скалярных произведений определяются из неравенства Вейерштрасса, откуда получим.

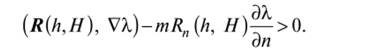
Выбрав такое напраатение нормали на произвольной кривой, используемой при построении неравенства Вейерштрасса, при котором R_n или дХ/дп обращаются в нуль, получаем, что в этом случае (fl (A_min, Я), VA,)>0, и здесь.

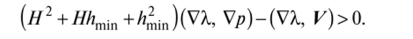
Это неравенство заведомо выполняется, если выполнены неравенства.

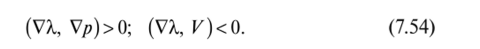
Неравенства (7.53) и (7.54) позволяют лишь утверждать, что там, где они выполняются, располагаются подобласти с h > 1 или h = 1. Но эти неравенства не позволяют сделать выводы о том, где располагаются такие подобласти, сколько их и как они соотносятся друг с другом. Ответы на эти вопросы может дать только рассмотрение полной системы необходимых условий, полученных ранее. При этом важнейшим является анализ решений краевых задач для функции X (7.37) и (7.44):

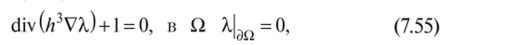
и уравнений Рейнольдса (7.32) и (7.33) для определения функции давления р. Это предполагает дополнительные знания о свойствах уравнений в частных производных эллиптического типа, к которым относятся уравнения для множителя Лагранжа X и уравнение Рейнольдса в данной задаче. Поэтому ограничимся здесь итоговыми результатами.

Начнем с того, что анализ свойств решений краевых задач (7.55) и (7.32)—(7.33) для множителя Лагранжа X и давления р позволяет сделать выводы о поведении градиентов VX и V/; на границе области ()Q при дополнительном предположении о гладком характере оптимального решения всюду за исключением угловых точек области Q. Отсюда же с учетом постоянства вектора Рможно сделать вывод о знаках скалярного произведения (VX, V). При этом в совокуп;

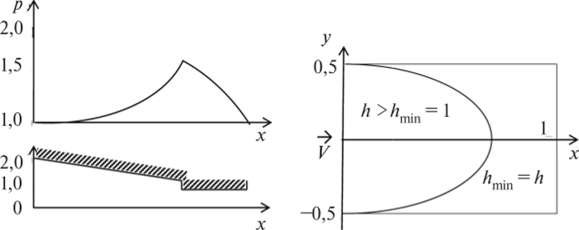
Рис 7.5. Оптимальные функциир и И

ности с условиями Эрдманна—Вейерштрасса (7.42) удается сделать важный вывод о существовании одной линии разрыва у управляющей функции И в области Я, которая отделяет область с h = 1 от области с h > 1. На рис. 7.5, в нижней его части, приведена проекция линии разрыва на плоскость (х, у), тогда как в верхней части представлены функция профиля h и поле давления р в центральной части, т. е. при у = 0. Видно, что в области с h > 1 давление нарастает, тогда как в области с h = 1 оно падает.

Пример 7.4. (периодическая пространственная вариационная задача Рэлея теории смазки [8]). Этим примером мы хотим показать те трудности, которые встречаются при решении пространственных вариационных задач. При этом разница постановок рассматриваемой задачи по сравнению с предыдущей казалось бы весьма незначительна, но эта разница кардинальным образом влияет на характер решения задачи.

Заменим в предыдущей постановке задачи краевое условие (7.33) — условие равенства избыточного давления нулю на границе — условием периодичности на передней и задней границах области Я, сохраняя его на боковых гранях. Условия периодичности по давлению должны быть дополнены условиями периодичности нормальной компоненты расхода. Таким образом, получим такую систему краевых условий:

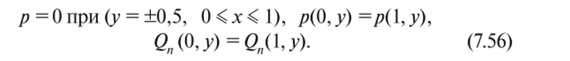
Принципиально вся система необходимых условий, полученная в предыдущей задаче, сохраняет свой вид, но здесь уже не удается получить важнейшие выводы о качественной форме оптимальной функции Их, у). При этом главная проблема состоит в том, что не удается установить кусочно-непрерывный характер функции Л* с конечным числом линий разрыва. Более того, при численном решении задачи с начальным приближением в виде одной линии разрыва возникает вторая такая линия, при увеличении же точности разностной схемы появляется еще одна и т. д. Таким образом, в данной задаче проявляется то, что принято называть «пространственным скользящим режимом», т. е. решение характеризуется бесчисленным множеством линий разрыва у оптимальной функции h и это решение уже не принадлежит не только классу непрерывных функции, но и классу кусочно-непрерывных функций. Этот класс функций и некоторые его свойства мы обсудим далее.

Очевидно, что подобная оптимальная функция Их, у) не может удовлетворять исходному уравнению Рейнольдса (7.32), решение которого уже при конечном числе линий разрыва у функции h становится проблематичным и не укладывается в рамки классического подхода, предполагающего, что h непрерывна со своими производными как минимум до первого порядка.

Изложенное требует пересмотра формулировки поставленной задачи, или, как принято сегодня говорить, расширения задачи. Рамки данной книги и проблемы, которые в ней обсуждаются, не позволяют подробно рассмотреть такое расширение постановки задачи и сопутствующие этой процедуре математические вопросы. Тем не менее приведем постановку и решение расширенной задачи, поскольку они демонстрируют важность подходов современной математики к решению задач инженерной практики.

Переходя к расширенной постановке задачи, начнем с того, что система уравнений Рейнольдса (7.32) заменяется следующим предельным^[1] уравнением:

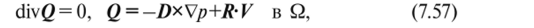
где D и R — симметричные матрицы второго порядка, которые запишем в виде.

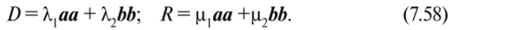
Здесь aawbb — диады (алЬ — собственные векторы матриц D и R. направленные по нормали и касательной в каждой точке линий разрыва предельной функции профиля Нх, у)); А, и Х₂, ц, и ц₂ — собственные числа, соответствующие собственным векторам А и В, зависящие от структуры оптимальной функции /г*.

В нашей работе [9] указан способ построения предельной функции h* с микрогеометрией, описываемой тремя функциями (%(х, у), Д (х, у) и Ь (х, у)) для микропериода, имеющего сечение прямоугольной формы.

Таким образом, симметричные матрицы D и R представляют собой некоторые обобщенные управления с элементами, описываемыми функциями х, А и |3, которые в нашей задаче являются управляющими. При этом оказывается, что во всех важных для практики случаях тройка функций х, А и |3 полностью описывает регулярную предельную микроструктуру (микропрофиль). Здесь под регулярностью понимается то, что все микропрофили одинаковы и предельная функция И" представляет собой совокупность их бесконечного множества на неподвижной поверхности. При этом возникает вопрос об ориентации этих микропрофилей. Выберем эту ориентацию такой, чтобы локальный угол (3 между направлением «оси» микропрофиля и направлением, обратным направлению скольжения (т. е. направлением, противоположным ос их), был острым, при этом саму функцию (3 определим в процессе решения задачи. Функцию х определим как предельную поточечную относительную ширину микропрофиля И₊, причем h₊ > 1 отвечает значению функции (глубине микропрофиля) А > 0, а 1 —х — отсутствию микропрофиля (гладкой области с h = 1 или, А = 0). При этом очевидно, что определенные таким образом функции удовлетворяют следующим ограничениям:

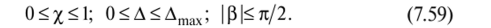
Теперь видно, что наша задача серьезно упрощается, поскольку она становится одномерной, так как исчезает зависимость функций X, А и (3 и отвечающего им предельного давления р в направлении х, совпадающем с направлением скольжения. При этом система уравнений (7.57) с коэффициентами (7.58) принимает вид:

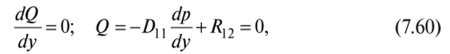
где скалярные коэффициенты D_u и R_n согласно [9] имеют вид:

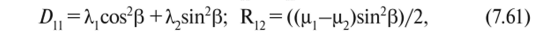
а постоянные величины X,, Х₂, ц, и (i₂ вычисляются по формулам.

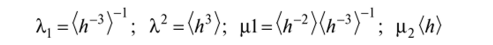
где символом k> обозначено интегральное среднее по элементарной области периодичности [9].

Нам остается найти их выражения через параметры микрогеомстрии, т. е. через определенные ранее управляющие функции х, Д и (3. Начнем с того, что определенная ранее И, такова, что если h = 1 в некоторой подобласти Q, то это равносильно тому, что здесь (Л_) = 1. Для <И₊) согласно [9].

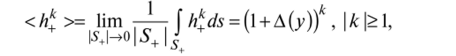
и окончательно получаем такое выражение для сглаженного (осредненного профиля):

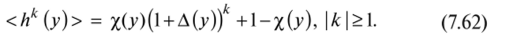
Таким образом определен вид всех величин X, Xj, р, и из (7.61) посредством предельных управляющих функций х (у), Д (у) и |3(у), и мы можем сформулировать следующую задачу оптимизации. Среди кусочно-непрерывных функций х, Д и |3, удовлетворяющих ограничениям (7.59), непрерывных функций р и чисел (9, являющихся решениями уравнений (7.60) с краевыми условиями.

найти те, которые минимизируют функционал.

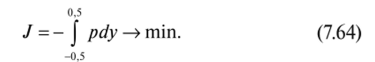
Анализ необходимых условий задачи показывает, что задача имеет два решения. Первое решение, которое назовем симметричным, отвечает значению расхода Q = 0 и соответствует шевронному профилю (рис. 7.6) с такими параметрами: х (у) ⁼ 0,500, Д (у) = = 2,653, (3(у) = ±0,2736 (±15,7°). Здесьзначение функционала (7.64) J = —0,2 279. Второе решение представляет собой односторонний профиль с микроканавками, расположенными в промежутке [—0,5;

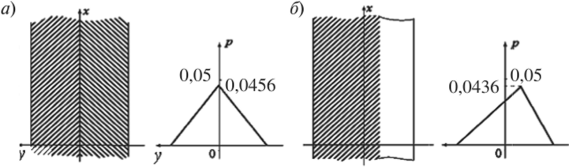
Рис. 7.6. Решения расширенной задачи: а — симметричное, б — одностороннее.

0,2292] или в промежутке [—0,2292; 0,5] (см. рис. 7.6). Здесь параметры. микрогеометрии такие: хОО ⁼ 0,6537, Д (у) = 3,189, |3(у) = = ±0,3773 (±18,2 °) и одинаковы при любом расположении микроканавок (как справа, так и слева по направлению скольжения). Значение функционала (7.64) /= —0,2 179.

В первом (симметричном) случае поле давления описывается формулой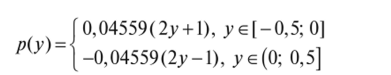

и имеет максимум, равный 0,4 559 в точке у = 0.

Во втором случае поле давления описывается формулой.

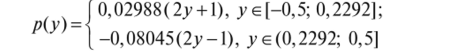
с максимумом в точке у = 0,2292, равным 0,4 357. Таким образом, «симметричное» решение дает лучшее значение функционала.

• [1] Предельным мы называем это уравнение потому, что оно не ограничивает нас в характере коэффициентов, в предположении, что это могут быть и функции с бесконечным числом разрывов в Q.