Процессы решения задач

Решение малых мыслительных задач

Хотя первоначально представители информационного подхода, а затем и когнитивной психологии предполагали добиться быстрых.

успехов в области изучения и моделирования мышления, реальные достижения оказались весьма скромными. Общее обсуждение процессов решения задач с позиций когнитивной психологии было дано Дж. Грино (Greeno. 1973). Согласно его определению, в случае решения задач «речь идет о нахождении способов трансформации исходной ситуации (или заданных переменных) в желаемую ситуацию (или неизвестные переменные)». Это понимание разделяют и другие авторы, в частности А. Ньюэлл и Г. Саймон, монография которых «Решение задач человеком» (Newell & Simon. 1972) длительное время считалась наиболее авторитетным руководством в данной области. Конечно, это определение недостаточно специфично, так что под ним могли бы подписаться представители всех направлений, так или иначе связанных с изучением мышления. При более детальном рассмотрении работ Дж. Грино, А. Ньюэлла, Г. Саймона и их коллег вновь вырисовываются очертания вычислительного устройства и его программного обеспечения.

Анализируя процесс решения задачи, Грино выделяет пять последовательных стадий:

• 1) чтение текста задачи;
• 2) интерпретация понятий;
• 3) извлечение релевантной информации;
• 4) создание плана решения,
• 5) выполнение вычислительных операций.

Эта модель становится более содержательной, когда Дж. Грино детально рассматривает стадию извлечения релевантной информации, выделяя в зависимости от характера этих процессов несколько типов задач: одни задачи требуют преимущественного извлечения правил оперирования (то есть процедурного знания), другие — хранящихся в памяти пропозиций (декларативного знания), третьи — дополнительной трансформации уже имеющихся знаний (то есть применения метапроцедур). Значительная часть усилий когнитивных психологов и специалистов по искусственному интеллекту была направлена первоначально на создание компьютерных моделей мыслительных процессов, типа глобальных когнитивных моделей, рассмотренных нами в начале этой главы.

Особой популярностью при моделировании мышления длительное время пользовались достаточно однотипные задачи на перемещения: анаграммы, задача переливания жидкости, задачи перевозки ревнивых мужей и их жен, миссионеров и каннибалов, проблема монстров и т. д. На рис. 8.3 показан вариант одной из наиболее известных из числа таких задач, получившей название «Ханойская башня». Задача состоит в том, чтобы переместить фишки с левого на правый стержень. При этом каждый раз можно брать только одну фишку, а класть ее можно только на фишку больших размеров. При оптимальной стратегии эта задача решается за 2п — 1 шагов, где п — число фишек. Детальный психологический анализ решения этой задачи проводился в последние десятилетия многими авторами, причем иногда ее используют и в целях нейропсихологической диагностики (в несколько упрощенных вариантах, известных как «Лондонская башня» и «Торонтская башня»).

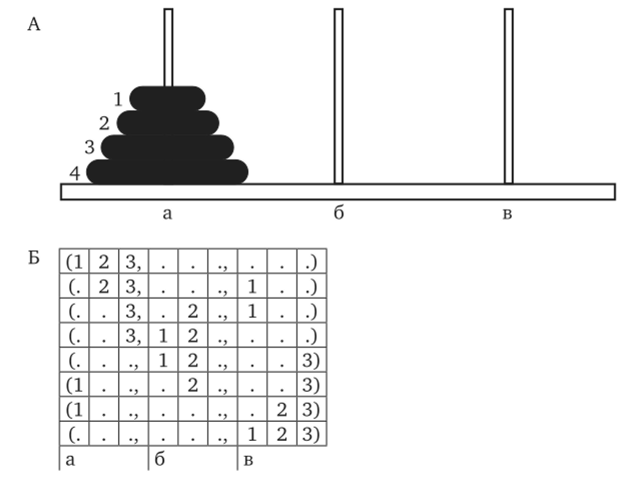
Рис. 8.3. Ханойская башня:

А. Исходное положение дисков;

Б. Алгоритм решения задачи для случая трех дисков Возможности машинных программ также часто проверяются на задачах этого типа. Г. Саймон и Дж. Хайес (Simon & Hayes. 1976) проанализировали для тестирования своей программы протоколы контрольной группы — людей, процесс решения задачи которыми прослеживался с помощью классической методики рассуждения вслух Дункера. Проведенный анализ показал, что испытуемые беспокоились о правильном понимании условий, часто просили дать им дополнительные разъяснения и проверяли допустимость тех или иных возможных шагов^[1]. Надо сказать, что именно эти моменты в работе программы представлены не были. Эквивалентность результатов, очевидно, еще не означает совпадения процессов. В целом ориентированный на формальное моделирование подход привел к успехам главным образом в случае тех задач, где относительно однозначно определены условия, а решение может быть достигнуто с помощью выполнения последовательных операций над дискретными символами.

Было бы большой ошибкой, конечно, недооценивать потенциал символьного подхода. Все более быстрый алгоритмический перебор вариантов — основа эффективности компьютерных систем, позволившая им в последнее время более чем успешно соревноваться с человеком даже в таких традиционных областях интеллектуальных достижений, как шахматы (см. 8.3.3). Человек должен решать задачи иначе, опираясь на эвристические методы. Не случайно отклонение от механического перебора считается одним из критериев действительно разумного решения. В популярной истории математики хорошо известен рассказ о юном Гауссе, нашедшем новое решение некоторой сравнительно легкой, но чрезвычайно скучной задачи. Согласно этой истории (или легенде), учитель, чтобы освободить себе какое-то время, дал школьникам задачу найти сумму всех чисел от 1 до 100. К его удивлению, уже через пару минут один из мальчиков — это был Карл Гаусс — сообщил, что задача решена. В отличие от прямого решения 1 + 2 + 3 и т. д. он выбрал непрямой путь, начав суммирование одновременно с двух концов ряда:

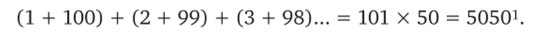
Определенные способности к манипуляции пространственными структурами, поиску решения «в обход», а не «в лоб», предполагаются множеством так называемых малых мыслительных задач, широко применяемых в психологии для иллюстрации закономерностей мышления. Рассмотрим следующую задачу, требующую известного переосмысления стратегии решения (задача упоминается в книге А. Р. Лурия 1979 года, посвященной мнемонисту Ш.). Пусть в университетской библиотеке на полке рядом стоят два тома руководства по когнитивной науке. Каждый том имеет объем 400 страниц. Червяк начинает работать с этим материалом и успевает за какое-то время продвинуться от первой страницы первого тома до последней страницы второго. Спрашивается, сколько всего страниц прогрыз червяк? Напрашивающийся сразу же ответ «800 страниц» ошибочен. Для решения нужно постараться наглядно представить, как именно будут стоять оба тома на полке при их правильной ориентации. Очевидно, первая страница первого тома и последняя второго будут разделены при этом только обложками. Следовательно, червяк прогрызет всего лишь две страницы.

В чем специфическая трудность этой задачи? Только в том, что, услышав в условиях данные о количестве страниц в сочетании с вопросом «сколько?», мы ошибочно интерпретируем эту задачу как математиче-^[2]

скую. На рис. 8.4 приведены две задачи «графическо-математического» типа, решение которых мы предоставляем читателю. Эта пара задач позволяет проиллюстрировать феномен функциональной фиксированности, который использовался гештальтпсихологами для критики взглядов представителей вюрцбургской школы (см. 1.3.1). Дело в том, что задачи несколько отличаются принципом их решения. При этом внешне они очень похожи, поэтому возникает впечатление, что во втором случае можно просто применить старое решение, или, иначе говоря, использовать опирающуюся на функции памяти метапроцедуру ВОСПРОИЗВЕДЕНИЕ, тогда как необходимыми являются ПОНИМАНИЕ и ВАРЬИРОВАНИЕ с одновременным подавлением (метапроцедура КОНТРОЛЬ) тенденции к повторению. В результате «фиксированности» на ошибочном подходе испытуемые тратят на решение второй задачи больше времени, чем на решение первой.

Большинство рассмотренных в этой главе задач решается легче, когда они даны на конкретном материале, что свидетельствует о роли процессов пространственного воображения. Для современных «эволюционистов» (см. 8.2.3) и сторонников концепции «телесной заземленное™» семантики (см. 7.4.2) это ожидаемый результат, объясняемый первичностью манипулятивной активности с предметами. Вместе с тем имеются и другие задачи, которые требуют абстрактно-символьного ОПИСАНИЯ условий. Опора на стратегию наглядного ПРЕДСТАВЛИВАНИЯ может вести при этом к выраженным ошибкам.

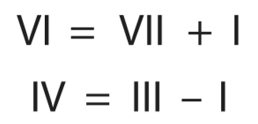
Рис. 8.4. Два ошибочных уравнения выложены из спичек римскими цифрами. Как исправить каждое из уравнений путем перестановки только одной спички?

Хорошим примером служит предложенная английским психологом Ричардом Грегори задача на определение толщины сложенного 50 раз пополам листа папиросной бумаги. Большинство испытуемых пытается наглядно представить процесс последовательного складывания очень тонкого и очень широкого листа. В этом случае они обычно называют величину порядка одного-двух метров. На самом деле в результате этой процедуры, по сути дела представляющей собой возведение двойки (с некоторым коэффициентом, равным толщине листа) в 50-ю степень, должна была бы получиться величина, сопоставимая с расстоянием от Земли до Солнца! В другой задаче того же общего типа испытуемым предлагается представить себе тонкий шнур, плотно опоясывающий Землю по экватору, а затем добавить к нему метровый отрезок. Необходимо определить примерную величину зазора между шнуром и земной поверхностью, возникающего в результате ослабления натяжения шнура. Читатель может самостоятельно найти решение этой задачи. Заметим только, что решение ведет к игнорированию размеров опоясываемого объекта: оно является тем же самым в случае Земли и теннисного мяча.

Рассмотрим еще одну задачу, известную как задача про безумного орла. Пусть в одно и то же время из города, А и города Б, расположенных на расстоянии 100 км друг от друга, навстречу друг другу отправляются два поезда. Скорость каждого из них равна 50 км/ч. В момент начала движения с паровоза одного из поездов взлетает орел, который летит навстречу другому поезду со скоростью 100 км/ч. Долетев до второго поезда, орел немедленно поворачивает назад и летит к первому поезду, от которого немедленно летит к другому и т. д. Спрашивается, сколько всего километров пролетит орел до момента встречи поездов? В подобной формулировке задача навязывает яркий зрительный образ летающего вперед и назад орла. Знающего математику человека это заставляет строить алгебраические уравнения, учитывающие постоянное сокращение расстояния между поездами. Задача решается тогда путем суммирования ряда чисел, соответствующих расстояниям, которые на каждом этапе пролетает орел. Правильное, то есть в данном случае простое решения состоит в… игнорировании траектории полетов орла. В самом деле, двигаясь с относительной скоростью 100 км/ч (50 + 50) поезда должны пройти 100 км. Следовательно, встреча произойдет через 1 час после начала движения. За это время орел пролетит точно 100 км.

Попробуем подвести некоторые предварительные итоги анализа решения задач. Уже в классической немецкой психологии мышление стало описываться как преобразование проблемной ситуации. Вюрцбуржцы подчеркивали при этом целенаправленность и абстрактный характер мыслительных операций, гештальтисты — спонтанность трансформаций, неожиданно ведущих к усмотрению решения, инсайту (см. 1.3.1). По сравнению с этими направлениями когнитивные исследования, во-первых, позволили описать эвристики, используемые в процессах решения (см. 8.1.1 и 8.4.1), и, во-вторых, добавили представление о множественном выборе: выборе формата репрезентации условий и выборе метаопераций, используемых для трансформации этих условий. Для успешности решения, следовательно, большое значение имеет соответствие представления условий тем метапроцедурам, которые используются для достижения решения.

Еще один существенный результат исследований последних лет состоит в выявлении коммуникативной природы мышления и, соответственно, многих возникающих при решении задач затруднений. В особенности малые мыслительные задачи, примеры которых были приведены на предыдущих страницах, специально сконструированы так, чтобы вводить читателя/слушателя в заблуждение, навязывая своими формулировками неоптимальные репрезентации и (или) средства их трансформации. В этом отношении использующие их психологи прямо нарушают один из грайсовских принципов коммуникативной прагматики, который предписывает говорящему быть релевантным (так называемая максима отношения — см. 7.4.1). Что касается испытуемых, то они значительно усложняют себе путь к решению, заранее ожидая поддержки со стороны экспериментатора и стараясь быть кооперативными: «Если экспериментатор сообщает мне все эти сведения, я должен обязательно попытаться использовать их в моем решении задачи».

Таким образом, мышление как решение задач — это прежде всего искусство выбора и отбора: выбора общего формата репрезентации условий и соответствующих метапроцедур, а также отсеивания (с кроющейся за ним метапроцедурой КОНТРОЛЬ) подчас очень заметных, но иррелевантных с точки зрения разрешения проблемы деталей. Подобное отсеивание иррелевантных и даже намеренно вводящих в заблуждение деталей делает возможной более полную концентрацию на существенных для решения моментах. Судя по всему, эти процессы по их значимости выходят далеко за рамки собственно психологических исследований малых мыслительных задач, представляя собой одну из основ значительно более сложных интеллектуальных достижений, например, открытий Коперника или Галилея. Ведь эти открытия противоречили не только общепринятому «академическому знанию», но и непосредственно наблюдаемым «физическим фактам», таким как видимое движение Солнца относительно неподвижного горизонта и, несомненно, более высокая скорость падения тяжелых тел по сравнению с легкими.

• [1] Подобные исследования справедливо критикуются за опору на рассуждениевслух. Согласно распространенной точке зрения, самоотчеты отражают лишь гипотезы, которые конструирует субъект, пытаясь дать причинно-следственное объяснение своегоповедения (см. 4.4.3). Параллельный анализ самоотчетов и движений глаз испытуемыхсвидетельствует о том, что лишь часть активности, связанной с процессами решениязадач, находит отражение в вербальных отчетах. Серьезная проблема состоит такжев интерференции рассуждения вслух с процессами самого решения (см. 1.1.3).
• [2] Наглядная интерпретация этой же задачи состоит в ее представливании каквыкладывания поверхности, состоящей из увеличивающихся на единицу рядов квадратов. Такая поверхность будет иметь форму прямоугольного треугольника. Удвоив числоквадратов, можно увидеть, что искомое решение эквивалентно нахождению половиныплощади прямоугольника со сторонами 100 и 101. Общее аналитическое решениядля подобного примера арифметической прогрессии, конечно же, выгладит следующимобразом: 0,5n х (n + 1).