Классическое определение вероятности

Допустим, что в картотеке содержатся истории болезней 7 пациентов, причем 2 из них — студенты, 5 — пенсионеры. Очевидно, возможность изъятия наугад истории болезни пенсионеров (событие А) больше, чем студентов (событие В). Здесь каждое событие обладает какой-то степенью объективной возможности, для сравнения которых введено число, характеризующее возможность появления события. Это число называется вероятностью события и обозначается Р или р.

Пусть в результате испытания из п равновозможных несовместных событий данное событие А происходит в т случаях, которые называются благоприятствующими.

Вероятностью события А называют отношение числа блаИсторически за этой формулой закрепилось название «Классическое определение вероятности».

Из определения вероятности следует, что вероятность случайного события А может принимать значения в пределах.

Если В — достоверное событие, то т = п и Р (В) = 1; если С — невозможное событие, то т = 0 и Р (С) = 0.

Пример 2.2. Из 35 больных, поступивших в хирургическую больницу за месяц, 7 человек имели травму. Какова вероятность поступления больных с этим видом заболевания?

Решение. Вероятность поступления больных с травмой (вероятность события А) в соответствии с классическим определением вероятности

Пример 2.3. В картотеке содержатся истории болезней 7 пациентов, причем 2 — студенты, 5 — пенсионеры. Найти вероятность изъятия наугад истории болезни пенсионера и студента.

Решение. Обозначим события: А — изъята наугад история болезни пенсионера, В — студента. Общее число равновозможных событий, (изъята история болезни) равно полному числу пациентов, т. е. п = 1. События несовместны, так как вынимается одна и только одна история болезни. Число благоприятствующих исходов изъятия истории болезни пенсионера (событие А) равно числу пенсионеров, т. е. т₁ =7. Вероятность того, что изъята история болезни пенсионера.

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">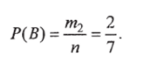

гоприятствующих случаев т к общему числу всех равновозможных несовместных событий п, т. е.

Аналогично рассуждая, получим, что вероятность изъятия истории студента.

Пример 2.4. Из 24 человек, одновременно заболевших острым респираторным заболеванием, 19 выздоровели полностью за 8 дней. Допустим, из 24 человек наугад выбирают 6. Какова вероятность того, что за 8 дней из этой выборки: а) 6 человек выздоравливают; б) никто не выздоравливает.

Решение. Обозначим события: А — за 8 дней выздоравливают 6 человек; В- за 8 дней не выздоравливает никто.

а) Общее число равновозможных несовместных событий равно числу сочетаний из 24 человек по 6.

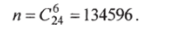
Число исходов, благоприятствующих событию А, равно числу сочетаний из 19 человек по 6, т. е.

Вероятность того, что за 8 дней выздоровели 6 человек.

б) Число исходов, благоприятствующих событию В, равно числу способов выбора шести не выздоровевших из шести человек, тогда т₂ =1.

Вероятность того, что за 8 дней из шести человек не выздоравливает никто

Пример 2.5. В группе 16 студентов, из них на «отлично» учатся 4 человека, на «хорошо» — 10, на «удовлетворительно» — 2. Найти вероятность вызова наугад любого из успевающих к доске.

Решение. Общее число равновозможных событий (вызов к доске) равно полному числу студентов, т. е. п = 16. События несовместны, так как вызывается один и только один студент.

Число благоприятствующих случаев вызова отличника (событие А) равно числу отличников в группе, т. е. т, =4. Вероятность того, что вызван отличник.

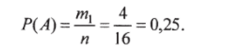
Число благоприятствующих случаев вызова студентов (событие В), успевающих на «хорошо», равно 10. Следовательно, Число случаев, благоприятствующих вызову студентов (событие С), успевающих на «удовлетворительно», равно /я₃ = 2. Искомая вероятность

Пример 2.6. На садовом участке перед посадкой случайно смешаны саженцы двух сортов яблонь: 7 саженцев сорта Афродита и 9 — сорта Солнышко. Какова вероятность того, что первыми будут посажены 4 саженца яблонь сорта Афродита?

Решение. Обозначим событие: А — первыми будут посажены 4 саженца яблони сорта Афродита. По условию в каждое множество из 16 элементов входят 4 элемента, причем порядок роли не играет. Тогда общее число равновозможных исходов испытания равно числу сочетаний из 16 элементов по 4:

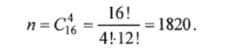
Благоприятствующими событию А будут множества из 7 элементов, в каждое из которых входят 4 элемента, причем порядок элементов не играет роли. Следовательно, число благоприятствующих исходов испытания равно числу сочетаний из 7 по 4:

Искомая вероятность того, что первыми будут посажены 4 саженца яблонь сорта Айюолита.

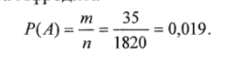
Пример 2.7. Для лечения болезни применяются пять лекарств d, е, f к, г. Врач хочет провести сравнительное исследование трех из этих лекарств, которые отбираются наугад из данных пяти. Какова вероятность того, что:

• а) будет исследовано лекарство d;
• б) будут исследованы лекарства d и е;
• в) будет исследовано по крайней мере одно из лекарств due. Решение. Пусть событие А — будет исследовано лекарство d,

В — будут исследованы лекарства dwe, C- будет исследовано по крайней мере одно из лекарств d и е. Ниже в таблице выписаны все 10 комбинаций из пяти лекарств по 3, т. е. число равновозможных несовместных событий п равно 10.

Исходные комбинации лекарств.

Событию А благоприятствуют 6 наборов лекарств, т. е. /и, = 6. Следовательно, Р (А) = т, In =6/10 = 0,6. Читателю предлагается самостоятельно найти Р (В) и Р©.

Описанная процедура с привлечением данных в виде таблицы применяется для нахождения вероятности сравнительно малого количества различных исходов испытаний.

Поэтому определим вероятности Р (А), Р (В) и Р (С) другим способом, используя результаты гл. 1. Число равновозможных, несовместных событий равно числу сочетаний из 5 лекарств по 3, т. е.

• а) Подсчитаем число исходов пц, благоприятствующих событию А. Среди 3 наугад взятых лекарств из 5 есть лекарство d и, следовательно, остальные 4 лекарства имеют другие обозначения. Значит, 2 лекарства из оставшихся 4 можно отобрать
• 2 41

С₄ = —— = 6 способами, т. е. т_] =6. Таким образом,.

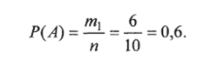
• б) Число исходов т₂, благоприятствующих событию В, рав-
• 2 3'

но числу сочетаний из 3 лекарств по 2, т. е. т₂ =С₃ = = 3. Тогда вероятность того, что в число отобранных лекарств попадут оба лекарства due

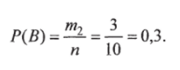
в) Число благоприятствующих исходов тз события С равно числу случаев, одновременно благоприятствующим событиям А и В, т. е. т₃ = гп +т₂ =6 + 3 = 9.

Следовательно,

Пример 2.8. В пульмонологическом отделении 12 больных, среди которых 8 человек с диагнозом — опухоль в легких, а остальные — плеврит. На процедуру наугад отобраны 9 больных. Найти вероятность того, что среди отобранных больных 5 человек с диагнозом опухоль в легких.

Решение. Обозначим событие: А — среди отобранных 9 больных имеется ровно 5 человек с диагнозом опухоль в легких. Общее число равновозможных несовместных событий равно числу случаев, которыми можно отобрать 9 больных из 12, т. е. С?₂ — числу сочетаний из 12 больных по 9.

Из 8 больных 5 с диагнозом опухоль в легких можно отобрать числом способов, равным числу сочетаний из 5 по 8, т. е. с|. Очевидно, среди 12 больных 4 человека с диагнозом плеврит (12−8 = 4), тогда число оставшихся больных с этим же диагнозом равно 4, т. е. 9−5 = 4. Число способов отбора 4 больных с диагнозом плеврит из 4 равно С*. Каждая комбинация из 5 больных с диагнозом опухоль в легких может сочетаться с каждой комбинацией из 4 больных с диагнозом плеврит. Таким образом, число благоприятствующих случаев, когда из 9 больных 5 окажутся с диагнозом опухоль в легких, равно произведению CgCf.

Подставляя данные примера, получим.

Получим решение в общем виде. Для этого обозначим через N — число больных в пульмонологическом отделении, п — число больных с диагнозом опухоль в легких, т — число отобранных больных, к — число больных с диагнозом опухоль в легких среди отобранных.

В принятых обозначениях обобщенная формула вероятностей принимает вид