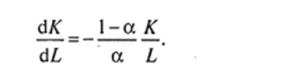Дифференциал функции нескольких переменных

Определение 4. Дифференциалом функции и = /(Л/), дифференцируемой в точке Л/(д, х_2У…, х_т), называется главная линейная относительно приращений AXj (/ = 1, 2, … т) часть (15.6) приращения этой функции в точке Л/.

Таким образом, с учетом теоремы 15.1 дифференциалом функции и = ДА/) в точке М называется выражение.

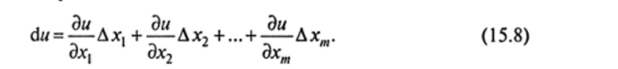
Назовем дифференциалами dx_j независимых переменных х_{ соответствующие приращения Ах_г Тогда формулу дифференциала функции нескольких переменных можно переписать в виде: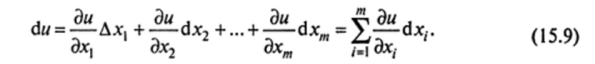

Отметим особо случай функции двух переменных и =/(х, у) се дифференциал в точке Л/(х, у) имеет вид:

Аналогично тому, как дифференциал функции одной переменной представляет собой в геометрическом смысле приращение «ординаты касательной», дифференциал функции двух переменных в этом плане является приращением «аппликаты касательной плоскости». Докажем этот геометрический смысл дифференциала функции двух переменных.

Покажем сначала, что касательная плоскость к поверхности в точке ЛГ₀(х₀, Уо> *o)> где го = /(*₀> Уо>* определяется уравнением.

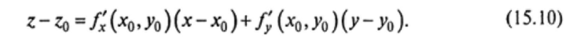
Как известно из аналитической геометрии, уравнение (15.10) определяет плоскость с нормальным вектором п = //"-!}" проходящую через точку.

%(х₀, У* *о)* ^ПУ^СТЬ Д* = х - х₀, Ау = у — у₀, Дг = z — Zq. Докажем, что угол ср между вектором п и вектором N₀N любой секущей, проходящей через точки N (x₀ + Ах, у₀ + Ау_у Zq + Az) и #₀, стремится к п/2 при N -" N₀ (рис. 15.2), где Ах и Ау — приращения соответственно аргументов х и у. Так как координаты вектора yV₀/V.

равны Ах, Ау и Аг, угол между векторами п и N₀N определяется по формуле.

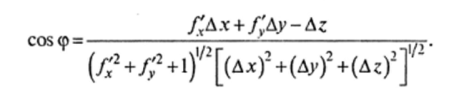
В силу соотношения (15.7) для случая функции двух переменных имеем: 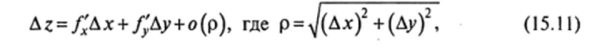тогда|сомр|<-^—^, т. е. cos ср 0 при р -> 0. Значит, при /V —> 7V₀

[р² + (д_г)²] ^р

• (согласно определению касательной плоскости) ф —> —, что и требовалось
• 2

доказать.

Поскольку приращение Дг «аппликаты касательной плоскости» определяется формулой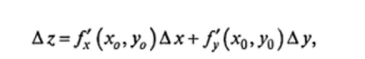

из равенства (15.10) получаем, что эта форма записи приращения совпадает с дифференциалом d г функции г = /(х, у) (см. формулу (15.9а)), что и определяет геометрический смысл дифференциала функции двух переменных.

Таким образом, из условия дифференцируемости функции двух переменных Z = /(х, у) в точке Л/₀(х₀, у₀) следует существование в точке W₀(x₀, у₀, го) касательной плоскости к поверхности, соответствующей этой функции.

Пример 6. Замена факторов по функции Кобба — Дугласа: установить, на какую величину следует изменить объем вложенного капитала К, чтобы при изменении трудовых ресурсов на AL выпуск продукции оставался неизменным. Функция Кобба — Дугласа имеет вид (п. 15.1.1, пример 5).

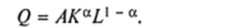
Полагая Q постоянным, получаем, что дифференциал этой функции равен нулю, т.с.

или.

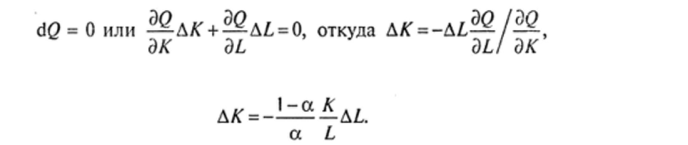
В относительных величинах мы имеем отношение соответствующих эластичностей:

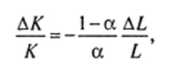
так что для компенсации изменения ресурса труда на 1% нужно изменить ресурс капитала на — -—— процентов. Из формулы для АКследует важное эконоа мичсскос понятие: предельная норма замены трудовых ресурсов L капиталом К_% которая равна: