Взаимное расположение прямой и плоскости

Пусть прямая и плоскость в пространстве заданы соответственно уравнениями.

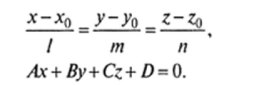
Параллельность прямой и плоскости. Прямая параллельна плоскости только в том случае, если направляющий вектор прямой перпендикулярен нормальному вектору плоскости. С учетом формулы (1.7) имеем условие параллельности прямой и плоскости:

Перпендикулярность прямой и плоскости. Очевидно, что прямая перпендикулярна плоскости лишь в том случае, когда се направляющий вскгср коллинеарен нормальному вектору плоскости. Тогда с учетом формулы (1.4) получаем условие перпендикулярности прямой и плоскости:

Угол между прямой и плоскостью. Под углом между прямой и плоскостью понимают острый угол, а между этой прямой и се проекцией на плоскость (рис. 14.5). Поскольку этот угол дополняет до п/2 угол между нормальным вектором плоскости и направляющим вектором прямой, согласно формуле (14.29) имеем:

Поверхности второго порядка

Поверхности, определяемые в прямоугольной системе координат алгебраическими уравнениями второго порядка, называются поверхностями второго

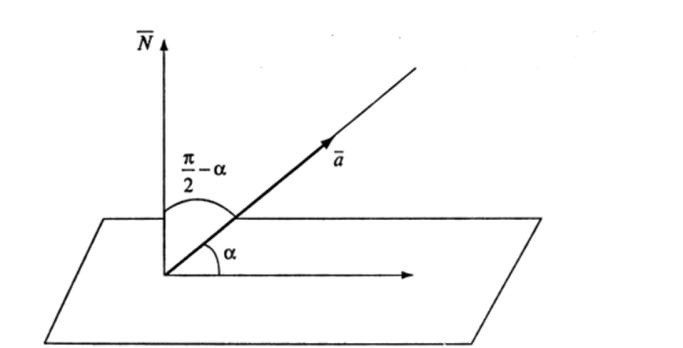
Рис. 14.5.

порядка. Поверхности второго порядка исследуют по их уравнениям с использованием метода параллельных сечений.

Эллипсоид. Каноническое уравнение эллипсоида:

В сечениях эллипсоида в плоскостях Оху и Oxz получаются эллипсы с парами полуосей соответственно а_у b и а, с (рис. 14.6), уравнения которых имеют вид:

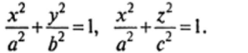
Числа a_ybwc называются полуосями эллипсоида. Нетрудно видеть, что самые большие эллипсы получаются в сечениях координатными плоскостями; по мере.

удаления от них эллипсы в сечениях плоскостями, параллельными координатным плоскостям, уменьшаются до вырождения в точку и полного исчезновения.

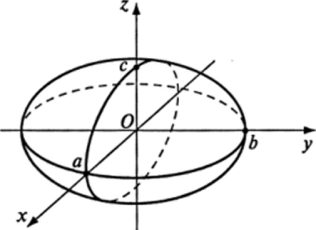
Однополостный гиперболоид. Каноническое уравнение однополостного гиперболоида:

^рис— 14.6 Вид этой поверхности показан на рис. 14.7. В сечениях однополостного гиперболоида координатными плоскостями Oxz и Oyz получаются гиперболы, уравнения которых соответственно имеют вид:

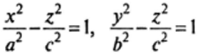
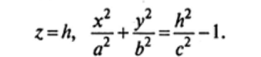
В сечениях данной поверхности плоскостями Z = Л, параллельными плоскости Оху, получаются эллипсы, полуоси которых увеличиваются по мере удаления от плоскости Оху. Наименьший эллипс лежит в координатной плоскости Оху; его уравнение имеет вид:

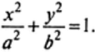
Положительные числа а, b, с называются полуосями однополостного гиперболоида. Сама поверхность имеет вид полости бесконечного протяжения по оси Oz, расширяющейся по мерс удаления от координатной плоскости Оху.

Двуполостным гиперболоид. Каноническое уравнение двуполостного гиперболоида (рис. 14.8):

Положительные числа д, Ь_% с называются полуосями двуполостного гиперболоида.

В сечениях этой поверхности координатными плоскостями Оху и Oyz получаются гиперболы, уравнения которых соответственно имеют вид:

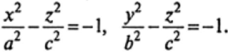
Сечения этого гиперболоида плоскостями Z = Л, параллельными координатной плоскости Оху, приводят к линиям пересечения, которые определяются уравнениями Нетрудно видеть, что эти уравнения имеют смысл при |Л| > с. Следовательно, в таких сечениях получаются эллипсы с полуосями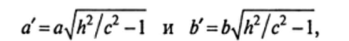

которые увеличиваются по мере удаления от плоскости Оху.

Таким образом, двуполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей типа бесконечных выпуклых чаш, которые расположены симметрично относительно плоскости Оху на расстоянии с от их вершин до этой плоскости.

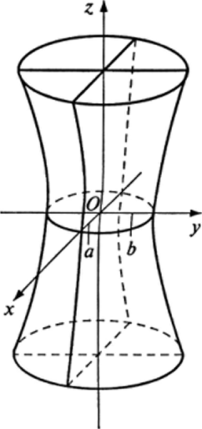
Рис. 14.7.

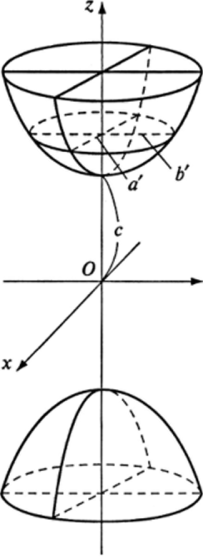
Рис. 14.8.

Из вида уравнения следует, что данная поверхность второго порядка расположена вдоль положительного направления оси Oz.

Рис. 14.9.

Эллиптический параболоид. Каноническое уравнение эллиптического параболоида (рис. 14.9):

где р > 0, q > 0 — параметры эллиптического параболоида.

Как и в предыдущих случаях, исследуем данную поверхность при помощи сечений. Сечения в координатных плоскостях Оху и Oyz имеют форму парабол с осью симметрии Oz их уравнения соответственно имеют пил!

Сечения данной поверхности плоскостями z = h приводят к эллипсам.

которые увеличиваются по мере удаления от плоскости Оху, с полуосями а' = yJTph и Точка 0(0, 0, 0) называется вершиной эллиптического параболоида. При р — q уравнение (14.39) определяет параболоид вращения, т.с. поверхность, образованную вращением параболы х² = 2pz вокруг оси Oz.

Гиперболический параболоид. Каноническое уравнение гиперболического параболоида (рис. 14.10):

где р > 0, q > 0 — параметры гиперболического параболоида.

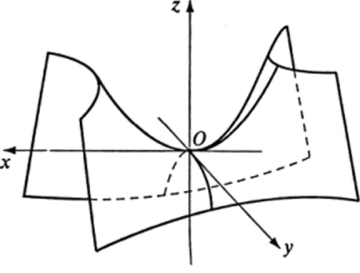
Рис. 14.10.

В ссчснии этой поверхности координатной плоскостью Oxz получается парабола.

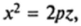
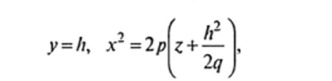
осью симметрии которой является положительная полуось Oz. В сечениях у = Л, параллельных плоскости Oxz, также получаются направленные ветвями вверх параболы вершины которых опускаются вниз вдоль оси Oz по мере удаления сечений от плоскости Oxz.

В ссчснии данной поверхности плоскостью также получается парабола.

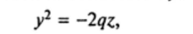
однако ее ось симметрии — отрицательная полуось Oz, т. е. эта парабола направлена вниз. В сечениях плоскостями, параллельными плоскости Oyz, также получаются параболы, направленные вниз, вершины которых опускаются вдоль оси Oz по мерс удаления сечений от плоскости Oyz.

Наконец, рассмотрим сечения этого параболоида плоскостями, параллельными плоскости Оху (г = h). Имеем уравнения.

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">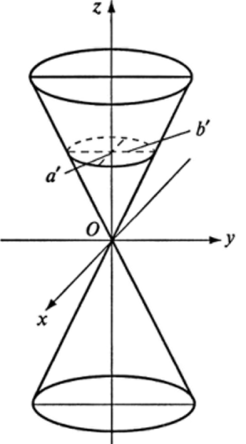

Рис. 14.11.

Таким образом, гиперболический параболоид представляет собой седлообразную поверхность, вершина которой находится в точке 0(0, 0, 0).

Конус второго порядка. Каноническое уравнение конуса второго_ порядка:

откуда следует, что при Л > 0 в сечениях получаются гиперболы, пересекающие плоскость Oxz при Л < 0 (вдоль отрицательного направления оси Oz) в сечениях получаются гиперболы, пересекающие плоскость Oyz. В самой плоскости Оху (при Л = 0) гиперболы вырождаются в пару пересекающихся прямых.

Поверхность конуса второго порядка показана на рис. 14.11.

В сечениях этой поверхности плоскостями Z = Л, параллельными плоскости Оху, получаем эллипсы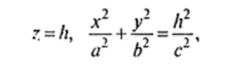

полуоси которых а' - ah/c и b' = bh/c увеличиваются по мере удаления сечений от плоскости Оху. При И = 0 линия пересечения конуса с плоскостью Оху вырождается в точку 0(0, 0, 0).

В сечениях данной поверхности плоскостями Oxz и Oyz получаем по паре пересекающихся прямых, соответствующие уравнения которых имеют вид:

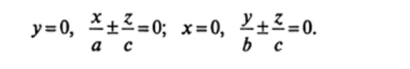
Упражнения Найти области опоеделения Функций.

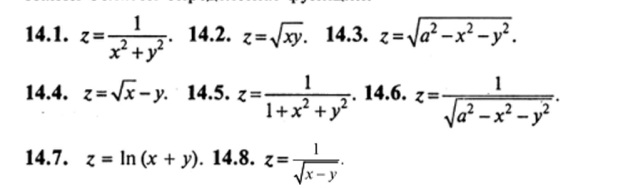
Построить линии уровня следующих функций. 14.14. Найти пределы функций:

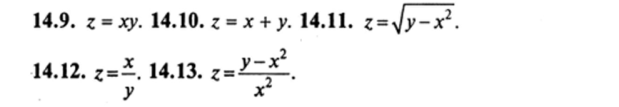
14.15. Показать, что функция f (x, y)=——— не имеет предела в начале коор;

х + у

динат.