Линейные дифференциальные уравнения второго порядка

Определение 2. Линейным дифференциальным уравнением второго порядка называется уравнение вида.

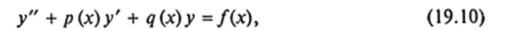
где у — искомая функция, а /?(х), q (x) и/(х) — функции, непрерывные на некотором интервале (а, Ь).

Если/(х) — 0, то уравнение (19.10) называется линейным однородным уравнением, в противном случае оно называется линейным неоднородным уравнением. Если разрешить уравнение (19.10) относительно второй производной, то легко увидеть, что оно является частным случаем уравнения (19.2) и удовлетворяет условиям теоремы Коши. Поэтому для любых начальных условий (19.3) при х₀ е (о, Ь) это уравнение имеет единственное решение задачи Коши.

Линейные однородные уравнения второго порядка

Рассмотрим свойства решений линейных однородных дифференциальных уравнений второго порядка.

Теорема 19.2. Пусть функции у₁ (х) и у₂(х) — решения уравнения (19.11). Тогда функция у = С₁у₁ (х) + С₂у₂(*) также является решением этого уравнения при любых постоянных С, и С₂.

Доказательство. Достаточно подставить указанную в условии теоремы функцию в уравнение (19.11) и собрать члены при С, и С₂ — это будут тождества, равные нулю, поскольку по условию теоремы у_{(х) и у₂(х) — решения этого уравнения. ?

Понятие зависимости функций было введено в п. 16.2.1. Напомним, что функции у,(х) и у₂(х) называются линейно зависимыми на (о, 6), если можно найти такие числа X, и Xj, нс равные нулю одновременно, что для любого хе (а, Ь) выполняется равенство.

В этом случае функции у,(х) и у₂(х) очевидным образом пропорциональны, например, yjy₂ = -Х₂/Х, = к при X, * 0 и у₂(х) * 0. Обратное также верно: если две функции пропорциональны на (о, b), то они линейно зависимы на этом интервале.

Если нельзя найти двух одновременно ненулевых чисел X, и Х₂, чтобы выполнялось равенство (19.12), то функции у_{(х) и у₂(х) называются линейно независимыми на (а, Ь). В таком случае эти функции уже не будут пропорциональными.

Введем определитель Вронского*, который для случая двух функций имеет вид.

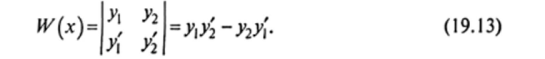
* Вронский Юзеф (1776—1853) — польский математик.

Теорема 19.3. Если функции ^(х) и у₂(х) линейно зависимы на интервале (а, b), то определитель Вронского, составленный из них, равен нулю на этом интервале; если же функции линейно независимы на (а, Ь)> то определитель Вронского отличен от нуля на (я, Ь).

Доказательство. Пусть у, и у₂ линейно зависимы на интервале (а, Ь). Тогда, как уже отмечалось, эти функции являются пропорциональными на (я, Ь)> т. е. у, = ку₂, а значит, и у-ку₂. Следовательно, в определителе IV (x) будут пропорциональные столбцы, что и означает его равенство нулю на интервале (а, Ь). Доказательство второй части теоремы проводится от противного.

Пустьу и у₂ линейно независимы на (я, Ь) предположим, что определитель V{x) равен нулю на этом интервале. Тогда столбцы IV (х) необходимо пропорциональны, т. е. пропорциональны и данные функции, что означает их линейную зависимость на (а, Ь) и противоречие с условием теоремы. Теорема доказана. В Оказывается, при решении уравнения второго порядка важно найти два линейно независимых решения, о чем говорится в теореме 19.4.

Теорема 19.4. Пусть решения уравнения (19.11) .у, (лг) и. у₂(х) линейно независимы на (я, Ь). Тогда функция.

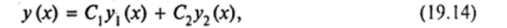
где С, и С₂ — произвольные постоянные, является общим решением однородного уравнения (19.11).

Доказательство. В силу теоремы 19.2 функция (19.14) является решением уравнения (19.11); нужно показать, что она представляет собой общее решение, т. е. что из этой функции можно выделить частное решение, удовлетворяющее любым начальным условиям (19.3).

Возьмем любые числа х₀ € (а, b), у₀ и у'₀ и составим из них начальные условия для решения (19.14):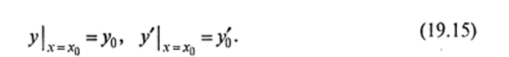

Подставляя в левые части этих условий функцию (19.14), получим систему двух линейных уравнений относительно неизвестных чисел С, и С₂:

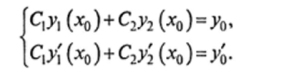
Определителем этой системы является определитель Вронского W (x₀), и в силу линейной независимости у_х и у₂ он не равен нулю, т. е. система имеет единственное решение С, =С,°, С₂ =С₂° при любых правых частях у₀ и у'₀. Подставляя эти значения в решение (19.14), получим частное решение, удовлетворяющее произвольно выбранным начальным условиям (19.15). Таким образом, решение (19.14) является общим для уравнения (19.11), что и требовалось доказать. ?

Рассмотрим примеры. Необходимо установить, будут ли указанные функции общими решениями уравнений (С, и С₂ — произвольные постоянные).

Пример 4. у = С, sin х + С₂ cos х, у" + у = 0.

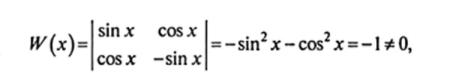
т.е. функция С, sin х + С₂ cos х является общим решением уравнения у" + у = 0.

Решение. По теореме 19.4 указанное решение будет общим для данного уравнения, если функции sin х и cos х являются решениями этого уравнения и линейно независимы. Поскольку (sin х)" = -sin х и (cos х)" - -cos х, обе функции являются решениями данного уравнения. Для установления их линейной независимости вычислим соответствующий определитель Вронского по формуле (19.13):

Пример 5. у = Cje²* + Cje³*, у"  — 5у' + 6у = 0.

Решение. Как и в примере 4, сначала проверяем подстановкой в данное уравнение, являются ли функции е²* и е³* его решениями:

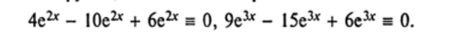
Затем вычисляем определитель W (x), составленный из этих функций:

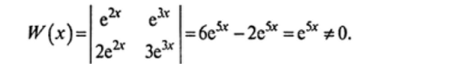
Указанная функция является общим решением данного уравнения.

Пример 6. у = CjX³/² + С₂, 2ху" = у 0 < х < 1.

Предлагаем читателю самостоятельно убедиться, что функции у, * х^3/2 и у₂ = 1 удовлетворяют данному уравнению и являются линейно независимыми, иными словами, что указанная функция представляет собой общее решение этого уравнения второго порядка.