Метод конечных разностей и его применение для стационарного режима

Для численного решения задач теплопроводности широко применяется метод конечных разностей, или метод сеток. Область непрерывного изменения аргументов х, у, г, т в этом методе заменяется сеткой — конечным (дискретным) множеством точек, называемых узлами. Разности значений одних и тех же аргументов для двух смежных узлов Ах, Ау, Аг, Ат называются шагами изменения этих аргументов. Шаги могут быть как постоянными, так и переменными.

Дифференциальное уравнение теплопроводности заменяется на сетке разностной схемой или уравнением в конечных разностях. После того как и краевые условия тоже заменены разностными схемами, получаем систему алгебраических уравнений в конечных разностях с числом неизвестных (температур), равным числу узлов сетки (уравнений).

Важнейшие свойства разностных схем — аппроксимируемость, устойчивость и сходимость [17].

Аппроксимируемость схемы означает, что при стремлении к нулю шагов аргументов решение системы алгебраических уравнений стремится к решению исходного дифференциальною уравнения при заданных краевых условиях.

Устойчивой называют схему, для которой ошибки округления при уменьшении шагов аргументов (сгущении сетки) не приводят к большим искажениям решения. В противном случае разностная схема называется неустойчивой.

Сходимость схемы означает, что при сгущении сетки решение системы алгебраических уравнений приближается (сходится) к решению дифференциального уравнения при заданных краевых условиях. Сходимость — одновременное следствие аппроксимируемости и устойчивости.

Рассмотрим метод конечных разностей для решения уравнения двухмерной стационарной теплопроводности в изотропном материале без источников теплоты (разд. 13.3). Уравнение имеет вид.

и называется уравнением Лапласа.

Выведем соответствующее ему уравнение теплопроводности в конечных разностях (разностную схему).

На теплопроводящую пластину (рис. 15.1, а), такую же, для которой было найдено аналитическое решение температурного поля (13.51), нанесена сетка; координаты точки О — X и Y; температуры в точке О и узлах сетки 1,2,3,4 обозначаем соответственно Го, Г), Гг, Гз, Г* (рис. 15.1, я, б, в). Градиент температуры в направлении оси х для точки О' (рис. 15.1, а) можно записать в виде:

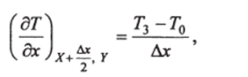
где члены высшего порядка малости не учитываются. Точность последнего равенства возрастает с уменьшением Дх.

Аналогично градиент температуры в направлении оси х для точки О" можно записать в виде:

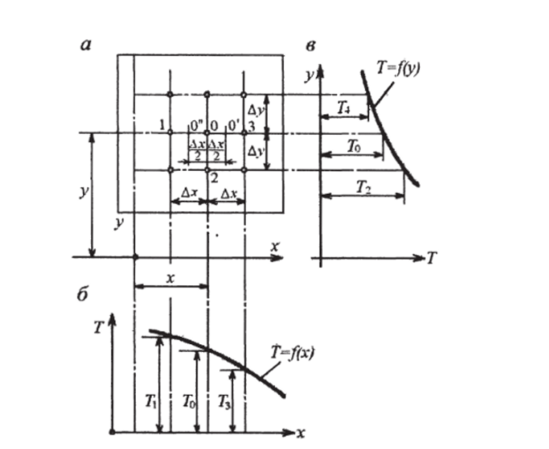
Рис. 15.1. К выводу уравнения (15.4) теплопроводности в конечных разностях для двухмерного температурного поля.

Вторая производная в направлении оси х для точки О:

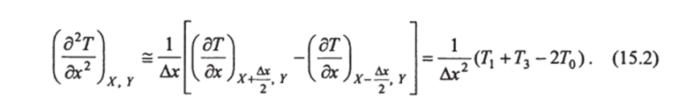
Вторая производная в направлении оси у для точки О (рис. 15.1, в):

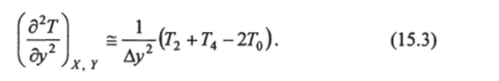
Подставив значения вторых производных из (15.2) и (15.3) в (15.1) и при условии Ах = Ду = Л, получим разностную схему откуда.

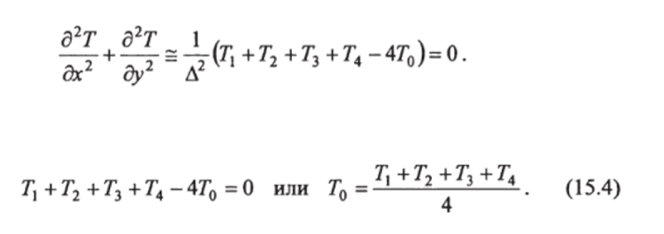
Из этого уравнения следует, что температура в любом узле плоской сетки есть среднее арифметическое температур в соседних четырех узлах сетки. Это одно из фундаментальных свойств уравнения Лапласа. Условие (15.4) положено в основу одного из методов численного решения задач теплопроводности, который называют релаксационным. Этот метод состоит в следующем. В узлах сетки записываются ожидаемые, но произвольно выбранные температуры. В общем случае они нс будут удовлетворять условию (15.4). Если То окажется больше среднего арифметического температур 7*1, 7*2,7з, Т₄, то это значит, что в точке О находится источник теплоты, если меньше — сток теплоты. В этих случаях разностная схема примет вид:

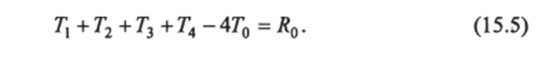
Величину Ro назовем остатком для точки О и запишем в виде.

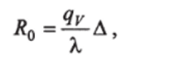
где q_y — объемная плотность теплового потока (раздел 13.2) в точке О; А — шаг сетки, при котором число узловых точек минимально.

Для всех узлов сетки найдем остаток Ro по уравнению (15.5).

О том, насколько точно были заданы значения температуры в узлах сетки, можно судить по величине остатка. Там, где остаток окажется наибольшим по абсолютной величине — значения температуры выбраны наименее удачно, т. е. они больше, чем во всех других узлах.

Пусть в точке О величина Ro наибольшая (рис. 15.1). Наибольший остаток делят на 4 и добавляют VaRq к остаткам соседних четырех точек, а температуру узла, где находился наибольший остаток, увеличивают на Уа первоначального остатка. Из уравнения (15.5) видно, что теперь остаток в узле О станет равным нулю:

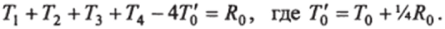
Остатки в точках 1,2, 3,4 увеличатся на VaRo, например в точке 1.

Далее все операции нужно повторить для следующего узла с наибольшим остатком. Этот процесс следует продолжать до тех пор, пока все остатки внутренних узлов сетки обратятся в нуль или будут пренебрежимо малы.

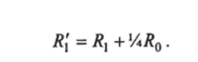
Результирующие температуры в узлах сетки составят искомое решение. Из сказанного следует, что время, затрачиваемое на решение задачи, будет тем меньше, чем удачнее выбраны ожидаемые температуры в узлах сетки.

Выбор этих температур удобнее проводить следующим образом. Вначале нужно нанести сетку с крупными ячейками и с малым числом узлов, или искомых температур. После решения задачи для крупной сетки нужно уменьшить размеры ячеек, а найденные в предыдущем расчете температуры использовать для нахождения температур в узлах второй (более мелкой) сетки. Продолжая этот процесс, можно достаточно точно и быстро определить температуры в узлах сетки, выбранной для решения конкретной задачи.

Условие (15.4) можно распространить на случай трехмерного температурного поля, для которого оно будет иметь вид:

а схема расположения узлов пространственной решетки дана на рис. 15.2.

Следует отметить, что релаксационный метод решения системы разностных уравнений трудно осуществим на вычислительных машинах, так как на них быстрее работать с уравнениями в циклическом порядке, нежели искать наибольшие остатки. Поэтому для расчета больших температурных полей (число узлов примерно более 20) целесообразнее использовать итерационные методы решения системы разностных уравнений (например метод Зейделя).

Следует отметить, что далеко не всегда измельчение сетки приводит при численном методе к уточнению стационарного температурного поля. Метод, используемый для решения, может оказаться при условиях конкретной задачи не;

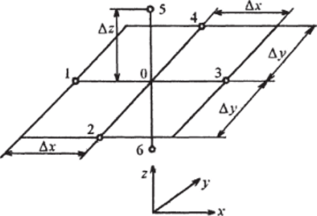
Рис. 15.2. Схема расположения узлов пространственной решетки трехмерного температурного поля устойчивым, т. е. при измельчении сетки будет давать решение, все более отличающееся от истинного. Поэтому для оценки точности численного решения при выбранном шаге и его проверки вообще целесообразно в нескольких узлах провести сравнение с аналитическим решением, если таковое существует.