Способы описания электротехнических и электронных устройств

Для анализа процессов в устройстве его представляют совокупностью моделей, отражающих свойства при заданной степени идеализации. Подходы к формированию различных моделей, в том числе компьютерных, базируются на совокупности математических моделей. Электротехнические устройства, в принцип работы которых заложены электромагнитные явления и эффекты, наиболее полно могут быть описаны с использованием методов электродинамики. В большинстве практических приложений допустимо применение методов классической электродинамики.

Задача расчета состоит в определении векторов электромагнитного поля, созданного с помощью не зависящих от исследуемого поля сторонних источников (например, тока с плотностью /_ст). Электромагнитное поле в сплошной вещественной среде описывается системой дифференциальных уравнений.

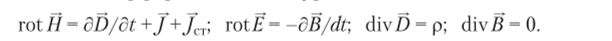
Приведенная система уравнений справедлива для описания электромагнитного поля в любом устройстве. Для получения единственного варианта решения, применимого для анализа конкретного изделия, общую систему уравнений Максвелла следует дополнить соответствующими граничными и начальными условиями.

При этом ycrpoiicTBo представляют в виде кусочно-неоднородной среды, параметры которой изменяются при переходе через поверхности, разделяющие отдельные области (части изделия). Постановка задачи анализа электромагнитного поля сводится к записи для каждой области уравнений Максвелла, дополненных соотношениями, характеризующими связи между векторами на границах раздела (граничными условиями) и значениями векторов электромагнитного поля для момента времени ф в каждой точке исследуемой области V (начальными условиями). Полученные на основании уравнений Максвелла условия для нормальных D_t«J», В_п и тангенциальных Е, Н, составляющих векторов электромагнитного поля на поверхности раздела вещественных сред можно представить в виде.

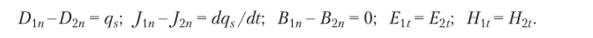
Математические трудности постановки и решения краевой электродинамической задачи, как правило, не позволяют получить обозримого аналитического результата. Обычно для устройства, содержащего несколько конструктивных элементов, даже весьма трудно найти единую систему координат, в которой могут быть записаны граничные условия на поверхностях раздела деталей.

Сложность общей постановки задачи приводит к необходимости принятия ряда допущений. Так, при анализе многих устройств характеристики материалов предполагают линейными: D = ее₀Е, В = р|д₀//,/= <�зЕ, что позволяет исходную систему привести к двум уравнениям для векторов напряженности магнитнойЯи электрической Е составляющих поля:

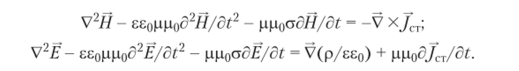
Распространенные математические методы решения краевых задач математической физики применимы для скалярных уравнений в частных производных. Поэтому вначале необходимо от исходных векторных уравнений перейти к совокупности эквивалентных ей скалярных. Указанная операция допускает простую реализацию только в декартовой системе координат.

Нашли применение также различные способы рациональной замены переменных для поставленной задачи. Так, при анализе нолей излучения и распространения электромагнитных волн в качестве переменных используют векторный А и скалярный <�р электродинамические потенциалы, определяемые выражениями.

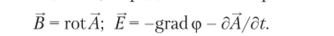
Их введение с использованием калибровки Лоренца 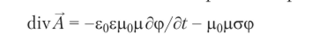приводит к системе с разделением переменных и источников поля.

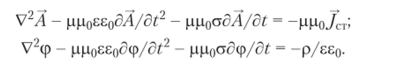
В случае анализа нестационарных режимов формируемая система уравнений в качестве независимой переменной также содержит время.

При наличии нескольких расчетных областей общая размерность системы уравнений имеет высокий порядок, что приводит к значительным математическим трудностям формулирования краевой задачи электродинамики и отсутствию единых регулярных методов получения аналитического решения. Это обусловило разработку подходов к составлению рациональной системы уравнений и их упрощению с помощью классификации электромагнитных полей, в основу которой заложены свойства источников электромагнитного ноля и окружающей их материальной среды.

По наличию источников выделяют задачи излучения электромагнитных волн и распространения электромагнитного поля. В зависимости от режима работы устройства различают неизменные во времени или синусоидальные источники. В соответствии со свойствами среды различают электромагнитные ноля в диэлектрических и проводящих средах.

Такой подход позволил выделить следующие группы частных случаев исследования электромагнитных полей:

• • волны в диэлектрической среде;
• • волны в проводящей среде;
• • волны в несовершенном диэлектрике (с потерями);
• • стационарные электрические и магнитные поля постоянных токов;
• • квазистационарные переменные поля;
• • статические электрические ноля.

Постановка и решение задачи нахождения электромагнитного поля излучающей системы имеет особенности в ближней, средней и дальней от излучателя зонах. Очевидно, что задача несколько упрощается, если исследуется только дальняя от излучателя зона. Когда расстояния между объектами излучения и приема значительно превышают длину волны, расчет можно разделить на следующие стадии:

• • определение поля, созданного излучателем (антенной) в однородной безграничной среде;
• • расчет распространения электромагнитной волны в пространстве;
• • определение вторичного поля, возникающего при падении на тело плоской электромагнитной волны.

Для расчета поля излучателя в линейной среде применяется принцип суперпозиции, состоящий в представлении поля излучения сложного источника в виде наложения полей излучения простых источников. Структура результирующего электромагнитного поля антенны определяется пространственным расположением элементарных источников и их свойствами. В качестве одного из распространенных типов элементарных источников используется электрический диполь с током i (t), поле которого зависит от времени и расстояния гот источника до точки наблюдения:/! = рр (р (? ^_ г/с)(Акг). Другим типом элементарного излучателя служит магнитный диполь, г. е. рамка малых размеров с током /'(/).

Каждая модель имеет ограниченную область применения и предназначена для исследования процессов в устройствах определенного класса.

Электромагнитные волны в диэлектрике при а = 0 описывают с помощью однородного уравнения для векторного потенциала.

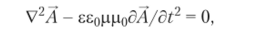
которое в декартовых координатах эквивалентно трем скалярным волновым уравнениям для составляющих А_х, А_у и А₂ вида.

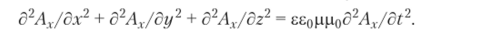
Дальнейшее упрощение модели состоит в переходе к одномерной задаче, т. е. предположении об изменении векторов вдоль одной координаты 2, приводящем к простой форме уравнения.

В декартовых координатах оно дает три идентичных уравнения вида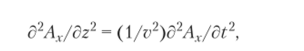

решения которых представляют собой совокупность распространяющихся вдоль оси z со скоростью v = 1/л/ее₀|ицо составляющих прямой F_nx(t — z/v) и обратной F_ox(t + z/v) волн.

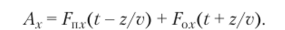
Решение векторного волнового уравнения получается объединением координатных составляющих А_х, А_у, А, и представляет собой суперпозицию векторных прямой F_n(t — z/v) и обратнойF₀(t + z/v) волн, причем вид функций F_u и F₀определяется граничными и начальными условиями.

Процессы в линейных системах удобно анализировать в частотной области с использованием преобразований Фурье. Представление синусоидальных составляющих с помощью комплексных изображений позволяет исключить время t и получить описание в форме обыкновенного дифференциального уравнения.

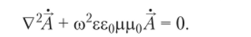
Для анализа переменного электромагнитного поля в проводящей среде при условии оЕ 3> seqdE/dt принимают допущение об отсутствии плотности тока смещения: е?₀ dE/dt = 0. В этом случае для областей, где нет сторонних источников (/_ст = 0) и отсутствует объемный заряд (р = 0), уравнение векторного потенциала имеет вид векторного уравнения теплопроводности.

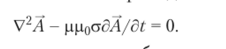
Использование комплексного изображения синусоидальных векторов в установившемся режиме позволяет свести уравнения поля к обыкновенному дифференциальному уравнению.

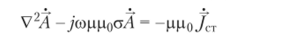
(здесь и далее через; обозначена комплексная величина, равная V-Г, так называемая мнимая единица), которое по форме записи подобно волновому уравнению для диэлектрической среды.

В случае плоского гармонического электромагнитного поля уравнение для напряженности электрического поля имеет вид.

где k = У/юйщ^ст = Vroppо<�т/2 (1 -j) = а (1 -;).

Из математики известна общая запись решения в форме.

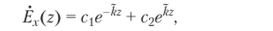
причем коэффициенты С и с₂ определяются из граничных условий.

Амплитуда составляющей E_x(z) = E₀e~^kz уменьшается по мере распространения с коэффициентом затухания е^-ez (например, на расстоянии 2₀ = 1/а она составляет 0,37 Еф). Неравномерное распределение плотности синусоидального тока по сечению проводника, т. е. уменьшение амплитуды по мере удаления от поверхности, называют поверхностным эффектом. Зависимость коэффициента затухания, а от частоты приводит к частотной зависимости сопротивления (R) и собственной индуктивности (L) проводника, например для шины прямоугольного сечения имеем R = со! = = (Ь/ й) л/<�орр (,/2а.

Анализ статических и стационарных полей значительно проще вследствие отсутствия^{зависимости} переменных от времени, т. е. выполнения условий BA/dt = 0, ду/Bt = 0.

К электростатическим относят поля, создаваемые в диэлектрической среде постоянными во времени и неподвижными в пространстве зарядами. Скалярный потенциал электростатического поля удовлетворяет уравнению Пуассона V²cp = -р/'сщ. Если известно распределение объемной плотности зарядов р (х_ш у_ю г_ы), то скалярный потенциал произвольной точки N (x, y, z) рассчитывается интегрированием по всей области источников (рис. 1.13, а):

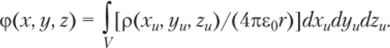
При необходимости расчета поля вне источников заряда для потенциала используется уравнение Лапласа У²ф = 0, и характер ноля определяется граничными условиями (p_t = (р₂, Zdq>/dt = 8₂б?(р₂ДЛ При исследовании векторных полей по найденному распределению в пространстве скалярного потенциала ф (х, у, z) для восстановления векторного поля Е (х, у, z) можно применить формулу Е = -grad (р, которая является следствием связи приращения потенциала с напряженностью электрического поля с/ф = -(Edl). Потенциал ф (х, у> z) в точке с заданными координатами определяется с точностью до произвольной постоянной ф₀, зависящей от выбора точки М отсчета потенциала:

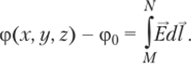
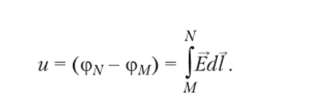
Это обусловлено тем, что посредством измерений однозначно можно определить только разность потенциалов, называемую напряжением, При исследовании электростатических полей следует выбрать координату отсчета потенциала ф₀ = 0 (обычно за нулевое принимают значение потенциала в бесконечно удаленной точке, что объясняется обратно пропорциональной зависимостью потенциала распределенного заряда от расстояния).

В реальных условиях расчет потенциала, созданного заданным распределением зарядов, осложняется наличием в пространстве.

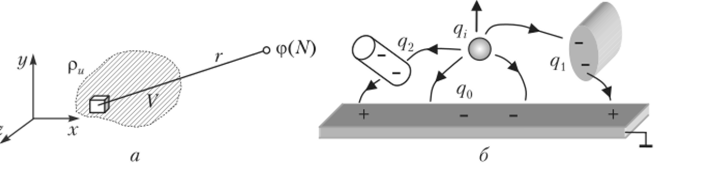
Рис. 1.13. Потенциал заряда в свободном пространстве (а) и при наличии проводящих тел (б).

проводящих тел, на поверхностях которых за счет явления электростатической индукции наводятся заряды (рис. 1.13, б). В линейной диэлектрической среде потенциалы проводников определяются как результат наложения электрических полей, созданных всеми k зарядами:

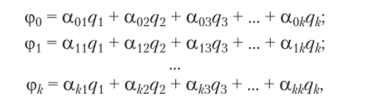
где а, — коэффициенты электростатической индукции (потенциальные).

Более распространено представление полученных уравнений, разрешенных относительно зарядов, и их запись через разности потенциалов, т.с. напряжения между проводниками при условии принятия нулевого значения потенциала одной из точек ф₀ = 0:

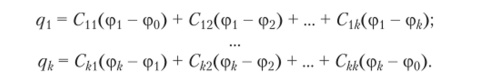
Соответствующие коэффициенты уравнений Су представляют собой частичные емкости в системе проводящих тел.

При наличии в диэлектрической среде двух проводящих тел говорят о конденсаторной емкости. Таким образом, определение емкости конденсатора состоит в постановке краевой задачи и расчете соответствующего электростатического поля.

Методы электростатики применяются для построения характеристик электронно-дырочных переходов, образующихся в области контакта полупроводниковых материалов с отличающимися параметрами. На основе явлений, возникающих при контакте материалов с отличающимися электрофизическими свойствами, реализуются самые различные электронные компоненты. В области контакта полупроводниковых областей пгипа с высокой концентрацией электронов (п_п ~ 10¹⁹ см^-3) ир-типа с концентрацией дырок р_р ~ 10¹³ см ³ за счет диффузии свободных зарядов и их рекомбинации вблизи контакта образуется слой, обедненный свободными носителями заряда и практически не проводящий электрический ток (рис. 1.14, а).

В этом слое образуется электрическое поле Е_т и создается потенциальный барьер ф₀. Подключение внешнего напряжения приводит к снижению барьера и образованию небольшого тока. Этот ток незначителен, пока приложенное напряжение меньше высоты потенциального барьера. Увеличение напряжения выше уровня отпирання перехода U* вызывает значительный рост тока (рис. 1.14,6). Изменение полярности приложенного напряжения приводит к повышению потенциального барьера и созданию через переход весьма малого обратного тока, обусловленного перемещением неосновных носителей зарядов, которые имеют незначительные концентрации. Существенное различие проводимости /?-«-перехода при прямом и обратном напряжениях обусловило его применение в качестве выпрямительного диода (рис. 1.14, в).

Анализ постоянных токов в проводящих и полупроводниковых структурах базируется па расчете стационарных (неизменных во времени) электромагнитных полей, созданных электрическими токами с постоянной плотностью,/.

В проводнике постоянный электрический ток образуется за счет потока, содержащего большое число носителей зарядов, и объем проводника остается электрически нейтральным. Для участков проводника, где сторонние токи отсутствуют (/_ст = 0), уравнения стационарного электрического поля подобны уравнениям электростатического поля при р = 0. Следовательно, при идентичных граничных условиях статические и стационарные поля обладают одинаковой конфигурацией и описываются подобными соотношениями. На практике это широко используется для определения одной из величин (например, емкости), если известна формула расчета проводимости.

В пространстве, окружающем неподвижные проводники с постоянными электрическими токами, возникает стационарное маг^ нитное поле. Для_его описания наряду с векторами индукции В и напряженности Я используется векторный магнитный потенциал, определяемый из соотношения В = rot А. Для вектора А выполняется уравнение У¹ А = -рр₀/, которое можно представить в виде скалярных уравнений для составляющих. Например, в декартовых координатах уравнения имеют вид.

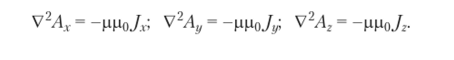
Рис. 1.14. Структурар-и-иерехода (а), его характеристика (б) и обозначение диода (в) Идентичность уравнений для составляющих вектора А и электрического потенциала в статике позволяет записать решения для составляющих по аналогии со статикой и затем получить векторное выражение посредством их объединения. При заданном распределении вектора J в области V векторный потенциал в точке наблюдения на расстоянии г от точки расположения источника с известной плотностью тока J вычисляют по формуле.

Важный для практики расчет магнитного поля, создаваемого постоянным током в длинном проводнике круглого сечения радиуса а, может быть выполнен посредством решения уравнения магнитного потенциала в цилиндрической системе координат с учетом симметрии, позволяющей предположить существование только составляющей А_г (рис. 1.15, а).

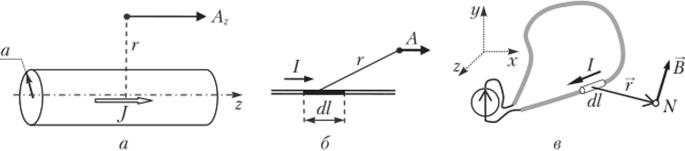
Рис. 1.15. Векторный потенциал проводов круглого (я) и линейного (6).

и контура (в) Уравнение имеет вид.

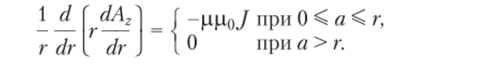
Напряженность магнитного поля имеет только составляющую #_а, которая определяется из соотношения H_a® = dAJdrw может быть представлена в виде #_а1 = (-рц₀./^г/2) — С/г, Н_а2 = ~с₂/г, причем С, с₂ определяются из граничных условий. При равномерном распределении тока I по сечению провода его плотность можно найти из формулы/ = //(7Ш²), и окончательные выражения имеют вид.

А_г = llW/(4rc)][ 1 — г²/а² — In (fl²/r₀²)]; Л_г2 = [цц₀//(4тг)]1п (а²/г₀²).

Вне провода векторный потенциал не зависит от его радиуса, что позволяет при расчете внешнего по отношению к проводу магнитного поля использовать приближение бесконечно тонкого проводника, называемого линейным проводом (рис. 1.15, б). Для отрезка линейного провода длиной dl с током I при учете равенства JdV= Id! векторный потенциал описывается выражением Л = рр₀/г7//(4л:г). При сложной конфигурации провода для определения векторного потенциала следует выполнить интегрирование по всей длине провода (рис. 1.15, в).

Магнитные ноля проявляются в форме их силового взаимодействия, которое испытывает каждый участок проводника. При сложной конфигурации контура для расчета воздействующих на него механических сил и вращающих моментов удобно воспользоваться энергетическим подходом. Заключенную в области пространства V энергию магнитного поля определяет выражение.

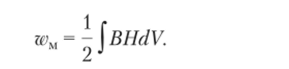
Магнитную энергию системы контуров с токами можно представить в виде произведения w_M = (½)ц// потокосцепления контура у и соответствующего тока /. Составляющая силы в направлении г определяется выражением F_r = dw_M/dr. Аналогично для составляющей механического момента по направлению, а (угла поворота подвижной части) имеем М_а = dw_M/da.

Магнитный поток Ф через поверхность s> опирающуюся на контур /, можно вычислить с помощью векторного магнитного потенциала: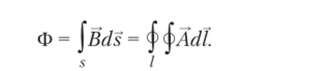

Расчет магнитных потоков необходим при анализе работы электромеханических преобразователей и устройств передачи (трансформации) электрической энергии, содержащих множество витков (контуров) типовых конфигураций. Простая конфигурация представляет собой систему двух плоских витков из тонкого провода (рис. 1.16, а).

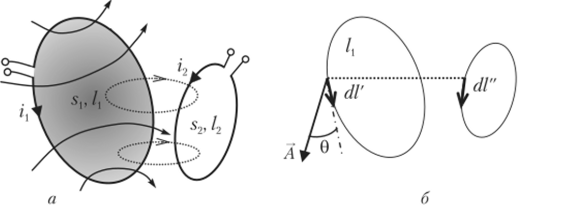
Рис. 1.16. Контуры из тонкого проводника (а) и схема для расчета взаимоиндукции (б).

Токи ц и i₂ создают в окружающем пространстве магнитные поля. Полный магнитный поток Ф_1? пронизывающий контур S, складывается из потока Ф_и, созданного током ц, и потока Ф₁₂, созданного током i₂. В линейной среде потоки пропорциональны создавшим их токам: Ф_и = Ь_{ц, Ф₁₂ = L_V2i₂. Таким образом, поток принято записывать в виде Ф[ = + L₁₂z₂, причем коэффициенты L и L_V2

называют соответственно собственной и взаимной индуктивностями.

Используя выражения потоков через векторный потенциал, для контуров из тонких проводников можно получить следующую формулу для расчета индуктивностей:

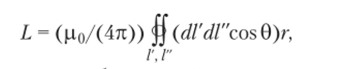
причем при вычислении собственной индуктивности элементы dl' и dl" принадлежат одному и тому же контуру, а при расчете взаимной индуктивности — разным (рис. 1.16, 6).

Приведенные способы расчета и полученные формулы справедливы, если ток неизменен для каждого сечения в любой момент времени. Эти условия выполняются в случае стационарных полей, создаваемых постоянными токами. При расчетах медленно изменяющихся переменных полей предполагают, что они квазистационарные (почти стационарные), т. е. в каждый момент времени пространственное распределение магнитного поля такое же, как при постоянных токах. Указанное условие выполняется, если, во-первых, можно пренебречь токами смещения между проводниками замкнутой электрической цепи и, во-вторых, длина проводников существенно меньше расстояния, на которое распространяется электромагнитная волна за временной интервал изменения поля.

Сложность краевых задач, а также ограниченность и невысокая точность получения аналитических решений обусловили применение численных методов анализа полей, сводящих дифференциальные уравнения в частных производных к системе алгебраических уравнений, которые решаются с помощью средств вычислительной техники. Выбор метода численного расчета представляет собой сложную проблему, зависящую от множества факторов, среди которых не последнюю роль играет размерность системы. Поэтому эффективны предварительные аналитические преобразования исходной задачи к удобной для численного анализа форме (упрощение постановки, декомпозиция объекта, аналитическое преобразование уравнений).

Наиболее распространенными при численном расчете являются методы конечных разностей (сеток) и конечных элементов, подходы к применению которых можно пояснить на примере анализа электромагнитного поля двухпроводного кабеля с металлической экранирующей оболочкой (рис. 1.17, а).

Метод конечных разностей базируется на замене дифференциального оператора разностным, позволяющим вычислить значения векторов поля в дискретном множестве точек в узлах сетки, которая заполняет непрерывную область исследования (рис. 1.17, б). Важным вопросом является выбор шага сетки и аппроксимация граничных условий в узлах сетки с целью обеспечения допустимой погрешности численного решения. Однако оценка указанной погрешности не может быть точно вычислена вследствие ее зависимости от характера исследуемого поля. Следовательно, при использовании численных методов для расчета электромагнитных полей требуется обеспечение устойчивости, сходимости и требуемой точности вычислительных методов.

В основу метода конечных элементов заложено разбиение исследуемой пространственной области на малые смежные подобласти, называемые конечными элементами, например прямоугольные треугольники (рис. 1.17, в). Внутри каждого элемента решение аппроксимируют с помощью простых универсальных функций координат (например, полиномиальными с неопределенными коэффициентами). Затем решения в отдельных элементах сопрягаются таким образом, чтобы обеспечить непрерывность искомой функции внутри области и заданные граничные условия. Записанные условия позволяют сформировать систему алгебраических уравнений относительно неопределенных коэффициентов. Геометрическая дискретизация области может быть проведена с учетом априорной информации о распределении поля в пространстве. Способ формирования аппроксимирующей функции может базироваться на вариационных или проекционных принципах.

Все электромагнитные явления наблюдаются в условиях движения, и, кроме того, практическое использование эффектов электромагнетизма, как правило, сопровождается перемещением час;

Рис. 1.17. Расчетная конфигурация (а), ее сеточная (б) и конечноэлементная модели (в) тей оборудования. Это требует в ряде случаев обращения к методам релятивистской электродинамики, базирующимся на неизменности полного заряда изолированной системы тел во всех инерциальных системах отсчета.

Решение проблемы силового взаимодействия между материальными объектами было дано А. Эйнштейном в специальной теории относительности, в которой для перемещаемых систем координат используются преобразования Лоренца, зависящие от относительной скорости движения р = v/c:

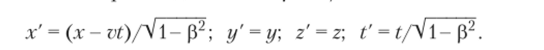
В рамках релятивистской электродинамики анализируются следствия изменения векторов электромагнитного поля при переходе от одной системы отсчета к другой, причем компоненты векторов электрического и магнитного полей преобразуются в соответствии с выражениями.

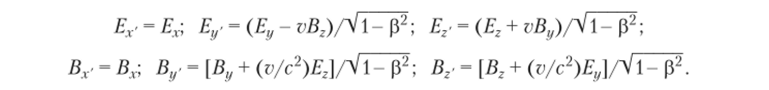
Объединив составляющие, несложно показать, что векторы напряженности электрического поля и магнитной индукции в одной системе представляют собой линейную комбинацию векторов в другой системе. Из этого следует важнейший вывод об относительности выделения из единого электромагнитного поля электрической и магнитной составляющих. Их соотношение определяется выбором инерциальной системы отсчета. Поэтому электрические и магнитные поля следует в общем случае рассматривать как полное электромагнитное ноле, проявляющееся в виде единого силового воздействия на заряженные частицы тела.

Преобразования Лоренца для векторов во взаимно перемещающихся системах координат позволяют записать уравнения электромагнитного поля, которые справедливы при любых скоростях взаимного движения материальных тел. При медленном взаимном перемещении систем координат (р = v/c 1) с достаточной точностью можно считать, что 1 — р² «1. При этом релятивистская запись уравнений электромагнитного поля приводит к уравнениям классической электродинамики.

Из специальной теории относительности вытекают два важных следствия, касающиеся зависимостей массы тела от скорости и энергии от массы. В классической механике инертная масса тела рассматривалась как неизменная величина — масса покоя т₀. Физики в экспериментах с быстро летящими электронами обнаружили возрастание релятивистской массы электрона при увеличении его скорости в соответствии с выражением.

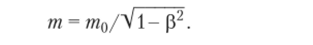
Очевидно, что частицы, обладающие массой покоя то, могут перемещаться со скоростью v < с, а частицы с нулевой массой покоя всегда движутся со скоростью света. С использованием формулы преобразования массы можно записать соотношения для вычисления импульса тела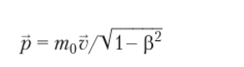

и действующей силы.

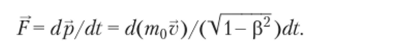
Соответственно, полная энергия движущейся частицы записывается в виде W = тс² = mocyVlр², а ее энергия покоя равна Wo = т₀с².

Последнее соотношение, характеризующее взаимосвязь массы и энергии, выполняется для изолированной совокупности частиц и материальных тел. Масса покоя тела и его энергия зависят от химического состава тела и его состояния. Понятие дефекта массы Ат применяется при анализе энергетических преобразований. Оно играет важную роль в атомной энергетике, определяя количество энергии, выделяющееся при атомных реакциях. В химических реакциях (например, сгорания топлива), при которых изменения претерпевают лишь молекулы вещества, в энергию превращается только весьма малая часть вещества. Как правило, незначительным является дефект массы при изменении состояния тела. Например, изменение температуры на 200 °C образца из железа массой 1 кг приводит к весьма незначительному изменению его массы — на 10 ¹⁵ кг.

Совместная формулировка законов передачи тепловой энергии (термодинамики) и электродинамики позволила сформулировать соотношения, связывающие электроэнергию с теплотой. Как известно, все тела, имеющие температуру выше абсолютного нуля, являются источниками электромагнитного излучения. Характер излучаемой энергии и ее взаимодействие с веществом во многом определяются диапазоном длин излучаемых волн. При этом возникает вопрос о механизме излучения электромагнитных волн светового диапазона. Были открыты фотоэлектрический эффект, явления поглощения света материальной средой, давления луча света и др., которые не могли быть интерпретированы на основе рассмотрения света как электромагнитных волн и требовали теоретического обоснования.

Объяснение излучений частиц, свойств света и других эффектов было дано в рамках квантовой электродинамики. Было установлено, что для создания электромагнитных волн с частотой видимого света размеры излучателя должны быть соизмеримы с габаритами атомов. Следовательно, источником светового излучения является движение заряженных частиц в атомах вещества. М. Планк предположил, что атом излучает электромагнитную энергию дискретно, т. е. отдельными квантами, энергия которых пропорциональна частоте излучения W/, = /Ь, где Й = 6,63 • 10 ³⁴ Дж • с — постоянная Планка. Наличие корпускулярно-волнового дуализма при описании явлений электромагнетизма следует из выражения импульса как отношения энергии электромагнитной волны к скорости ее распространения.

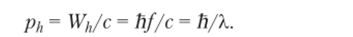
Гипотеза М. Планка была дополнена А. Эйнштейном предположением о локализации квантов в пространстве. Это означает, что, с одной стороны, свет можно рассматривать как непрерывно распространяющиеся в пространстве электромагнитные волны малой длины, а с другой стороны, энергия волны сконцентрирована в весьма малых областях пространства и способна оказывать физическое воздействие на окружающую среду. Иными словами, свет можно также рассматривать как поток световых квантов (фотонов), движущихся со скоростью света.

Из приведенных рассуждений следует, что любое излученное антенной электромагнитное поле наряду с волновыми обладает дискретными (корпускулярными) свойствами. Однако в области радиочастот энергия отдельных квантов настолько мала, что ее невозможно зарегистрировать опытным путем. При экспериментальном исследовании фиксируется большое число случайным образом возникших квантов, которое проявляется как непрерывная электромагнитная волна. Поэтому эффект квантования излучения можно наблюдать только на очень больших частотах излучения, т. е. при малых длинах волн.

В теории относительности фотон рассматривается как особый тип частицы, у которой отсутствует масса покоя. Масса фотона в соответствии с уравнением Эйнштейна определяется выражением.

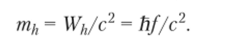
Наличие у движущегося фотона массы т_} и импульса р/, объясняет эффект давления света. Излучение и поглощение фотонов происходят при изменении состояний элементарных заряженных частиц на атомном уровне. К их описанию неприменимы как законы механики Ньютона, так и соотношения классической электродинамики Максвелла. Например, волновые свойства частиц не позволяют применить к ним понятие координат, так как сочетание «координата волны» лишено смысла. В соответствии с соотношением неопределенностей одновременно нельзя точно указать координату и импульс частицы. Их можно определить только с некоторой вероятностью.

Основы квантовой механики, базирующиеся на постулатах Н. Бора, соотношении неопределенности В. Гейзенберга, уравнениях Л. Эйнштейна и Э. Шрёдингера, были разработаны в первой половине XX в. Соотношения квантовой механики описывают только вероятность различных исходов опыта и, следовательно, имеют стохастический характер. Движение заряженной частицы в силовом поле характеризуется волновой функцией, представляющей собой решение уравнения Шрёдингера.

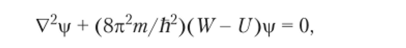
где v|i (x, у_у г, t) — волновая функция; W — энергия электрона; U (x, у у Zy t) — потенциальная функция, Объяснение электрофизических свойств материалов и описание процессов образования зарядов могут быть выполнены с использованием методов квантовой теории. Для анализа излучения энергии движущимися электронами используется модель атома, базирующаяся на следующих постулатах:

• • атомы могут находиться только в стационарных состояниях, в которых электроны движутся, не излучая, по разрешенным орбитам, каждой из которых соответствует свой уровень энергии;
• • при переходе атома из одного стационарного состояния в другое испускается или поглощается квант энергии.

Описание процессов на атомном уровне основано на гипотезе Луи де Бройля, который предположил, что материальное тело обладает сочетанием волновых и корпускулярных свойств, т. е. любое тело массой т, движущееся с постоянной скоростью v_y излучает электромагнитные волны длиной X = h/{mv). Иными словами, он распространил свойства фотонов на объекты, обладающие массой покоя, и в том числе на электроны.

С использованием сформулированных правил можно вычислить основные характеристики атома: радиус стационарной орбиты электрона и его скорость, энергию и частоту кванта излучения. Достаточно просто это можно проиллюстрировать на примере атома водорода, имеющего единственный электрон, который может находиться на одной из стационарных орбит с радиусами г_ьг₂ или г₃ (рис. 1.18, а).

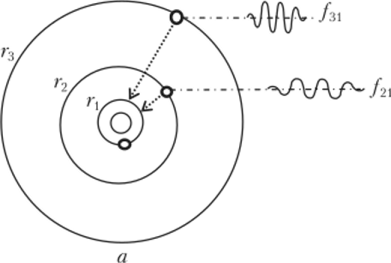
Рис. 1.18. Квантовая модель атома («) и энергетическая диаграмма (б).

При этом устойчивым является состояние электрона с минимальным запасом энергии, называемое основным или нормальным. Все другие разрешенные состояния называются возбужденными, т. е. электрон может попасть на них в результате некоторого воздействия. Время нахождения атома в возбужденном состоянии составляет порядка 10^-8 с. Из возбужденного состояния, характеризуемого энергией W_n, атом самопроизвольно переходит в основное состояние с энергией W с испусканием кванта й/= W_n — W, причем частота излучения зависит от начальной энергии электрона.

Каждый атом спонтанно излучает кванты света независимо друг от друга. Результирующее оптическое излучение имеет характер некогерентных колебаний, представляющих собой совокупность гармонических сигналов с произвольными значениями начальных фаз. При распространении в пространстве такие сигналы претерпевают значительное затухание.

Возможен также механизм вынужденного, или стимулированного, излучения, заключающегося в том, что под воздействием внешнего сигнала накачки большинство электронов переводится в возбужденное состояние на одну из орбит. Когда их число достигает определенного уровня, происходит испускание квантов на одной частоте и с одинаковыми значениями начальных фаз. Работающий на этом принципе прибор получил название лазера (Light Amplification by Stimulated Emission of Radiation).

Излученные кванты взаимодействуют с веществом. При попадании квантов света внутрь вещества происходит их поглощение, которое может вызвать различные эффекты. Проявление эффектов взаимодействия света с веществом зависит от химического состава, агрегатного состояния и электрофизических свойств материалов.

Электродинамическое описание электрических устройств является базовым при их анализе. Во-первых, функционирование многих электрических и электронных аппаратов (полупроводниковые приборы, электрические датчики физических величин, электродвигатели) может быть объяснено только на основе взаимодействия электромагнитных и других физических полей. Во-вторых, синтез эквивалентных электрических схем и определение параметров компонентов выполняются с использованием результатов расчета распределения электрического и магнитного нолей. Кроме того, без исследования создаваемых электрическими устройствами и электронными приборами электромагнитных полей невозможно проанализировать и оценить электромагнитную совместимость аппаратуры.

Вместе с тем высокая конструктивная сложность электротехнического и электронного оборудования, а также математические трудности анализа векторных полей привели к интенсивному развитию направления теоретической электротехники, называемому теорией электрических и магнитных цепей. На начальном этапе развития электротехники такому подходу способствовало изготовление устройств с использованием соединенных проводниками элементов, сосредоточивших преимущественно один способ преобразования энергии. При исследовании подобных устройств применяется их описание в форме электрических эквивалентных схем, процессы в которых характеризуются зависящими от времени скалярными электрическими величинами (токами, напряжениями).

Наличие в электротехнических устройствах магнитопроводов из ферромагнитных материалов, концентрирующих индукцию магнитного поля, позволило упростить процедуру анализа за счет использования модели магнитной системы в вид с магнитной цепи.

Контрольные вопросы и задания

• 1. Дайте определение электромагнитного поля.
• 2. При каких условиях электромагнитное поле имеет характер плоской волны?
• 3. Сформулируйте основные подходы к классификации электромагнитных воли.
• 4. Каким образом в электродинамике учитывают электромагнитные свойства материальных сред?
• 5. Какие признаки используют при классификации материальных сред (веществ)?
• 6. Как формулируется полная постановка краевой задачи классической электродинамики?
• 7. На чем основано выделение частных случаев электромагнитных полей? Перечислите их типы.
• 8. Каковы условия, позволяющие перейти от электродинамического к схемотехническому описанию электромагнитных устройств?