Методы производящих и характеристических функций

Аппарат характеристических и производящих функций оказывается конструктивным и образует методы, состоящие в использовании свойств этих функций для решения конкретных задач теории вероятности:

• • МПФ — метод производящих функций;
• • МХФ — метод характеристических функций.

Метод производящих функций

Определение 3.1. Пусть СВ ?, > 0, — целочисленная, р*. = Р (% = к), где k — целое число; Х/Ф = 1, тогда производящей функцией случайной величины % называется функция R.

Свойства производящих функций.

1. (p_?(.v) определена в каждой точке отрезка [-1; 1] (так как.

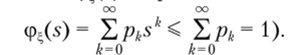
• 2. cfx (l) = 1 (так как cp-.(l) = Хр* =1).
• 3. Производящая функция qx (s) взаимно однозначно соответствует вероятностям {р_к = P (t, = к)}.

Доказательство. Утверждение следует из формулы (3.1) и единственности разложения в ряд Тейлора. Напишем ряд разложения функции Ф=(л) в нуле (ряд Маклере на):

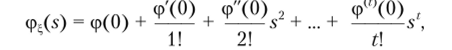
откуда из сравнения с определением производящей функции.

^-'.

следует, что р, =-. ,)та формула дает возможность пересчитывать из.

f!

производящей функции ряд распределения. Кроме того, эта формула наряду с определением производящей функции устанавливает взаимно однозначное соответствие между разными формами задания закона распределения рассматриваемых СВ в виде ряда распределения и производящей функции.

П

4. Если г) = X {<^} — независимые случайные величины, тогда.

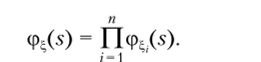
/=1.

Доказательство. По определению.

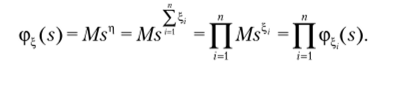
5. Если? = Е Я;?; + {?,•} — независимые случайные величины,.

i-i.

тогда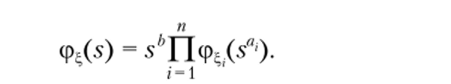

Доказательство. По определению 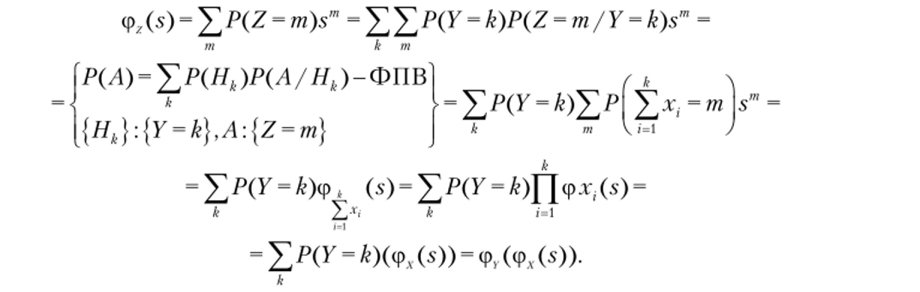Y

6. Пусть Z = YjXj, где {X,} — независимые одинаково распреде;

/=1.

ленные случайные величины, {X,} и У — независимые, целочисленные, для них известны производящие функции: (p_A(s) и фy (s). Тогда Ф/О) = Фг (ф00);

Доказательство. Выполняем преобразования:

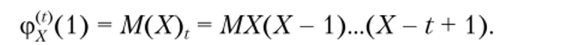
7. Связь производящей функции с моментами:

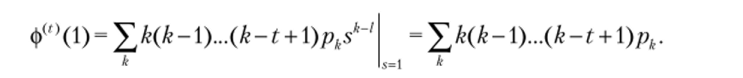
Доказательство. Возьмем производную от ф ($) = и подставим.

к

значение 5= 1:

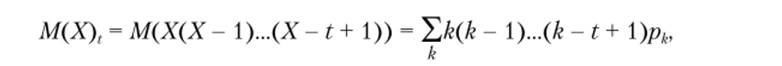
В то же время (X), = Х (Х — 1)…(Х — t + 1), откуда.

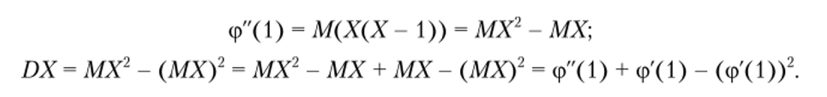
что совпадает с преобразованием левой части доказываемой формулы. Выпишем выражения для MX и DX через ф (5).

Из равенства ф⁽⁰(1) = М (Х), следует, что MX = ср'(1);

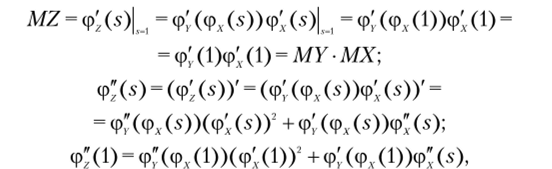
У.

8. Моменты случайного числа случайных слагаемых. Z =? Х".

!-1.

где {X,} — независимые одинаково распределенные случайные величины, (XJ и У — независимые, целочисленные и неотрицательные, и для них известны производящие функции _A-(s) и.

MZ и DZ через соответствующие моменты MX, MY, DX, DY, которые при заданных.

x(s) и ф,{л) легко вычисляются по предыдущему пункту.

Из п. 6 известно, что ф/(х) = ф)-(ф_Л(х)). Из п. 7 известно, что MZ= ф^.(1), DZ= ф" (1) + ф'(1) — (ф" (1))²— Поэтому.

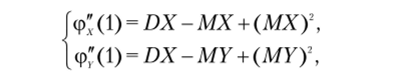
откуда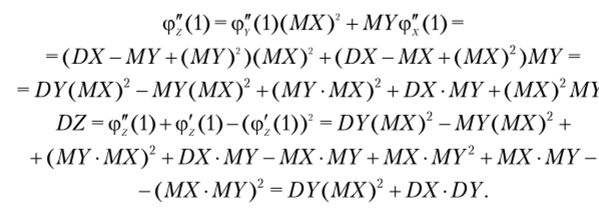

где dx = _Фд,(1) + _Ф;_у(1) — (Фх (1))²; dy= _Ф;<1) + ф^(1) — (фГ (1))²;

Г.

Производящие функции хвостов Определение 3.2 (общее определение производящей функции последовательности). Пусть а₀, а_ь … — последовательность действительных чисел. Если ряд.

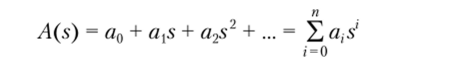
сходится в каком-нибудь интервале s₀ < s < s_u то /l (.v) — производящая функция последовательности {а,}, или производящая функция хвостов.

Пусть pj = Р{Х =j}, q₎ = P{X >j), j = 0, 1, 2,… Тогда {p,} — распределение вероятностей, так как ?/?, = 1, а {с/,} не является расиреде;

j

лением вероятностей, так как > 1.

Для k>0 имеем q_k=p_k+i + р_к!₂ + •••; при к = 0 q₀ = р, + р₂ + … = 1 — р₀. Составим функции.

р₀ + p_ts + p^s² + …; для ряда Q (.v) = q₀ + + q_ts + <7г5² + …

Оба ряда сходятся хотя бы при |s| < 1, поэтому.

X, a Q (s) — производящая функция последовательности чисел {q,}.

Теорема 3.1. При -1 < s < 1.

Доказательство. Коэффициент при 5^я в разложении по степеням s вы;

оо со ражения (1 — s)Q (s) равен q" - q", =? А — X Р, ⁼ -р," если п > 1,.

i=n+1 i=n

и q₀ = Pi + р, + … = 1 — р₀, если п = 0; коэффициент при s" в разложении, но степеням s выражения (1 — q>(.v)) есть -р" при п > 1 и 1- р₀ при п = 0. Таким образом, коэффициенты при 5^я совпадают, откуда и следует утверждение теоремы.

Теорема 3.2. MX = Q (l); DX= 2Q'(1) + Q (l) — (Q (l))², где MX и DX — соответственно математическое ожидание и дисперсия СВ X.

Доказательство. Известно, что MX = ф ((1) и ОХ = ф" (1) + ф'(1) ;

• — (ф'(1))'- Тогда, но формуле (3.2) ф () = 1 — Q (.*)(l — s); фЧ Д = Q (s) —
• — (У ООО — s); ф'(1) = Q (l) => имеем

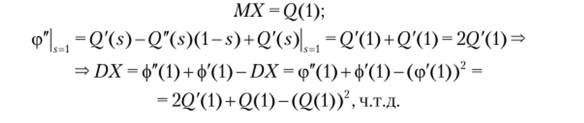
Примеры решения задач на производящие функции Применение метода производящих функций рассмотрим в задачах.

Задача 3.1. Получить вид производящей функции для следующих распределений: а) В (, р) б) В (п, р); в) гс (?0;^г) G (p)'> д) сдС (д); е) Па (г, р); ж) ОВ (г, р).

Решение

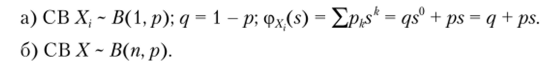
• 1- й способ. X = 2 Xj, где {X,} — независимые одинаково распреде-
• 1−1

ленные по В (1,р) случайные величины. Поэтому, но свойству 4 cp^s) = «Фаг, — = (ps + q)

2- й способ. Можно.

x (s) вычислить непосредственно:

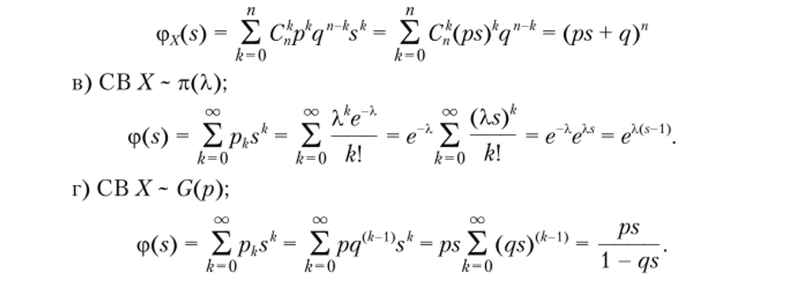
Задание 3.1. Получите вид производящей функции для следующих распределений: а) сдС (р); б) Па (г, р); в) ОВ (г, р).

Указание. Для б) и в) используйте их связи с распределениями г) и д) задачи 3.1 и воспользуйтесь свойством 4.

Определение 3.3. Композицией законов распределения называется закон распределения суммы независимых случайных величин с соответствующими законами распределения. С использованием свойства 4 задачи для композиций решаются просто.

Метод производящих функций состоит в использовании перечисленных свойств производящей функции.

Задача 3.2. Найти композиции и моменты для следующих законов распределения: X ~ n (Xi)_t Y ~ л (Х₂) (случайные величины X и У независимы).

Решение

Я"As) = Ф)0) =.

_+y(.v) = => закон распределения СВ X +Y — rc (A,_t + Х₂).

Задание 3.2. Найдите композиции и моменты для следующих законов распределения: X ~ В (п_ир)_} YВ (п₂, р) (случайные величины Хи Y независимы).

Задача 3.3. Вычислить моменты распределения СВ X ~ В (п_ур). Решение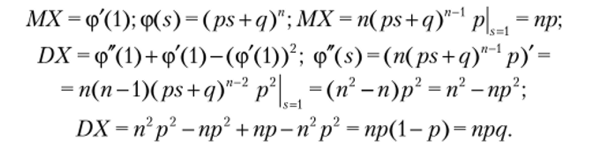

Задание 3.3. Вычислите моменты распределений: а) X ~ 5(1, р);

6) X ~ п (Х); в) X — G (p); т) X ~ сд6'(р); д) X — Па (г, р) е) X — ОВ (г, р).

Задача 3.4. Найти распределение и моменты случайных величин Z структуры свойства б для X — тт (Х,), Y ~ В (п, р).

Указание. При решении используйте свойства 6 и 8.

Решение

Y

Z = 2 Х" где {X,} — независимые одинаково распределенные СВ,; = 1.

{X,} и У — независимы. (p_v(.s) = е^ф1)

(ps + q)" <�р^s) = ф_Л(ф)(^Л')) ⁼ = (ре^к{-⁾ + q)"  — производящая функция случайных величин Z, или закона распределения случайных величин Z. Моменты:

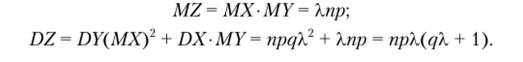
Задание 3.4. Найдите распределение и моменты случайных величии Z структуры свойства 6 в случаях: а) X — 7t (X,), Y ~ п (Х₂); 6) X — G (p), Y~ В (п, р) — в )Х~В (п, р), Y ~ Па (г, р) г) X ~ OB (r, р), Y ~ В (1,р).

Задача 3.5. По заданной производящей функции ф (х) найти закон распределения дискретной СВ X.

Решение

Ответ можно получить, разложив ПФ в ряд Маклорена. Получаем.

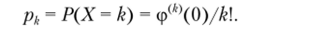
(Это значит, что задание производящей функции эквивалентно заданию закона распределения дискретной СВ.).