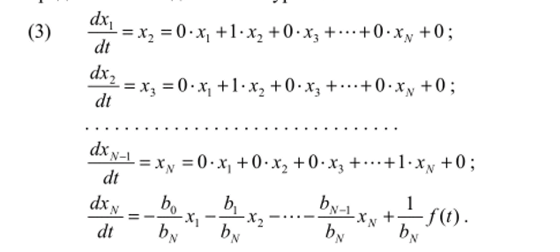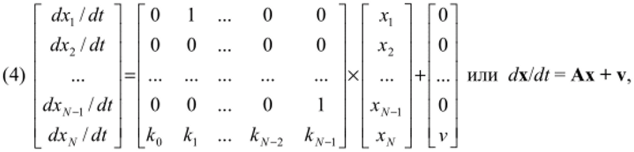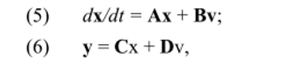Метод переменных состояния

Особенности описания цени. В качестве переменных помимо контурных токов и узловых напряжений могут быть выбраны такие переменные, при которых вместо рассматриваемого выше дифференциального уравнения N-ro порядка описание цепи сводится к системе уравнений в нормальной форме (или форме Коши). Каждое из уравнений в форме Коши:

=> содержит в левой части только первую производную соответствующей переменной *"(/);

=> не содержит в правой части производных и является линейной функцией только выбранных переменных x_a(t) и приложенных к цепи сигналов v_m{t).

Представим в форме Коши дифференциальное уравнение N-ro порядка с известной правой частью, записав его виде ция, или отклик цепи.

Введем новые переменные как совокупность вспомогательных функций.

Используя функции (2), дифференциальное уравнение (1) можно представить в виде системы уравнений.

В справедливости (3) нетрудно убедиться, подставляя в последнее уравнение системы х = у, затем лг₂ = dxldt = dy/dt, х₃ = dxildt = Sx! df" = cPyldt² и т. д. Последняя подстановка x_N = d x_N__x!dt = ]х= d^y/dt^¹ с учетом того, что dxsjdt = axldi = dyldr, приводит к исходному уравнению (1).

Систему функций (2) можно рассматривать как некоторый вектор состояния х (0 с координатами jci,., х, принадлежащий пространству состояний рассматриваемой динамической цепи.

Представим (3) в матричной форме.

где k_r = г = О, 1,.N-2, N-; v =//Ьц‘, А — матрица NxN; х — вектор-столбец переменных состояния; v — вектор-столбец внешних воздействий.

В общем случае описание цепи сводится к двум системам уравнений, имеющим в матричной форме следующий вид [17]:

где.

=> х = х (/) = [xi (/)_# Xi (t), …, дгд{0]^т — N-мерный вектор переменных, компоненты которого *"(/) называют переменными состояния;

=> v = v (/) = [vj (/), v₂(i), …, v_M(t)Y — ^/-мерный вектор входных воздействий (параметров независимых источников напряжения и тока);

=> у = у (/) = [)'|(0″ Уг (0>? Ук (0Г —/^-мерный вектор выходных параметров (искомых токов и напряжений);

=> А, В, С, D — матрицы с вещественными элементами размера NxN, NxM, KxN, КхМ соответственно.

Переменные состояния x"(t) полностью определяют реакции (отклики) всех ветвей цепи при заданных начальных условиях и приложенных при t > to внешних воздействий. Использование их позволяет составить систему.

(5) из наименьшего числа переменных. Число (N) уравнений в нормальной форме (или число переменных состояния) определяет порядок дифференциального уравнения цепи. Решения уравнений (5), (6) могут быть представлены во временной области через матричную экспоненту и в частотной области в виде передаточной матрицы [17].