Оптические методы обработки информации

Оптическая обработка информации основывается на использовании оптического излучения как носителя информационного сигнала и оптических элементов для обработки этих сигналов.

Оптические сигналы

Характерной особенностью оптических сигналов является их двумерность. Это свойство связано с малой длиной световой волны (= 0,4 + 1,5 мкм).

Оптический световой диапазон неоднороден и подразделяется на поддиапазоны (рис. 9.1).

Рис. 9.1. Шкала оптического диапазона. Частота излучения в оптическом диапазоне составляет — 10^1S Гц. энергия излучения лежит в диапазоне 10—1 эВ Для количественного описания оптического излучения пользуются параметрами, соотношения между которыми приведены в табл. 9.1.

Атомы вещества излучают короткими сериями— волновыми пакетами. Длительность волнового пакета и спектр излучения взаимосвязаны: чем больше длительность волнового пакета, тем уже спектр излучения. Это следует из теоремы Фурье, согласно которой любую конечную и интегрируемую функцию можно представить в виде непрерывной суммы бесконечного числа синусоидальных компонент. Колебание F (t)_y вызванное прохождением цуга волн, можно представить как суперпозицию монохроматических колебаний с различными частотами v.

Тогда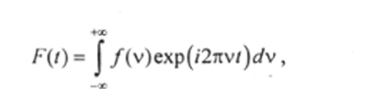

где.Ду) определяет распределение по амплитуде монохроматических составляющих F (t). Распределение этих составляющих по энергиям дается выражением [Ду)|². В соответствии со свойствами преобразования Фурье можно произвести обратное преобразование и получить спектр функции F (t). Действительно.

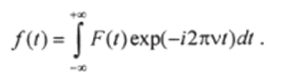
Таблица 9.1. Фотометрические параметры излучения.

На рис. 9.2, а приведены функции Fl), описывающие волновые пакеты и соответствующее распределение энергии (интенсивности f) по частоте (рис. 9.2, б).

Рис. 9.2. Соотношение межау длительностью волнового пакета и его спектром излучения.

Особый интерес представляют монохроматические или когерентные сигналы.

Когерентность— явление коррелированного протекания во времени и в пространстве колебательных или волновых процессов, позволяющее получить при их сложении четкую интерференционную картину.

В общем случае световые колебания частично когерентны и количественно когерентность измеряется степенью взаимной когерентности. Эта величина определяется контрастом интерференционной картины. Так интенсивность света в некоторой точке от двух монохроматических источников интенсивностью 1 и /₂ определяется выражением:

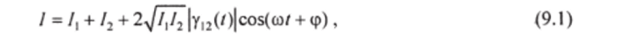
где |у,₂(/)| — степень взаимной когерентности, являющаяся функцией расстояния между источниками и времени распространения света, (р — фаза колебаний. Если !_у = /₂, то.

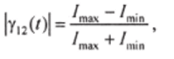
где /_т4х и /_тj" — интенсивности светлой и темной полосы интерференционной картины. Время когерентности т₀ определяется как минимальная задержка между интерферирующими световыми волнами, снижающая значение у (/) до заданной величины, включая нуль. Величина т₀ меняется в широких пределах: от т= 10 ¹⁵ с для солнечного света до т = 0,1 с для лазерного излучения высокой степени когерентности.

Длина когерентности /₀ = ст₀ также меняется в широких пределах.

Введем понятие оптического сигнала как электромагнитную волну, в которой в каждой точке пространства электрическое и магнитное поле меняется по гармоническому закону:

У, 0 = А (х, y) cos[2jtvf + ф (х, y)]_f (9.2).

где U (x, у, /) — скалярная функция координат пространства и времени, А (х, у) — амплитуда колебания напряженности электрического поля, v — частота колебаний, ф (дг, у) — фаза световой волны.

Рассматривается только электрическая составляющая электромагнитной волны, поскольку именно вектор Е ответственен за фиксацию электромагнитной волны квадратичными детекторами (глаз, фотопленка, фотоприемник). Можно записать световой сигнал в комплексной форме, удобной для сложных математических операций.

U{x, y, 0 = А (х, y) exp{i[2xvt + <�р (х, у)]}. (9.3).

Величину Цх, у, /) = А (х, у)-ехр[/<�р (х, .у)] называют комплексной амплитудой, которая основывает пространственное распределение амплитуды А (х, у) и фазы.

у) световой волны.

Временной множитель exp (2rcv/), который является гармонической функцией времени, опускают. Однако он может быть введен на любом этапе математических преобразований.