Наблюдаемость линейных стационарных систем

Рассмотрим линейную стационарную управляемую систему.

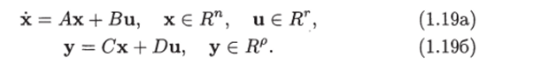
Введем в рассмотрение матрицу.

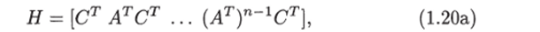
которая называется матрицей наблюдаемости. Эта матрица состоит из столбцов матрицы С^Т и столбцов произведений матриц А^ТС^Т, (А^Т)²С^Т, (А^т)^п~¹С^т и имеет размерность (п х рп). Наряду с матрицей наблюдаемости рассмотрим транспонированную матрицу наблюдаемости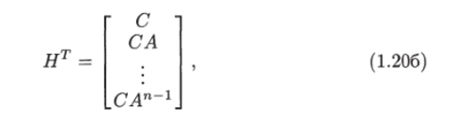

которая имеет такой же ранг, что и исходная матрица Я.

Управляемая система (1.19) вполне наблюдаема (восстанавливаема) тогда и только тогда, когда ранг матрицы наблюдаемости (1.20а) или, что-то же, ранг транспонированной матрицы (1.206) равен п.

Необходимость. Пусть ранг матрицы Н^Т меньше п. Тогда размерность пространства Я#, порожденного строками матрицы Н^т, меньше п, т. е. Rh является собственным подпространством пространства Rⁿ. Поэтому существует ненулевой вектор х± € Я^п, ортогональный всем вектор-строкам матрицы Н^т (таким вектором является любой вектор из Rⁿ, не принадлежащий подпространству Rh)‘-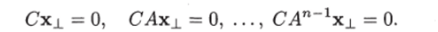

Как было показано, основываясь на теореме Кэли-Гамильтона, матрицы А^к при к^п линейно выражаются через I, А, …, А^п~¹₁ поэтому из приведенных равенств получаем, что СА¹х± = 0 при всех I = 0,1,2,… Следовательно, имеем.

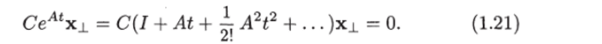
Пусть некоторому начальному условию х (0) = соответствует выходной вектор у^(0* ^ силу соотношения (1.21) всем начальным значениям фазового вектора вида х^ + xj_ соответствует один и тот Это и доказывает невозможность определения состояния х (?о) по значениям выходного вектора, если ранг матрицы наблюдаемости меньше п.

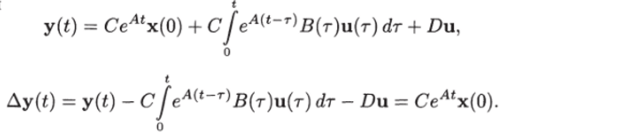
Достаточность. Пусть ранг матрицы управляемости равен п. В силу стационарности управляемой системы достаточно показать возможность определения состояния х (0) по известным значениям выходного вектора и управления на некотором интервале [0, ?1]. Имеем или Так как у (t) и и (?) доступны измерению, матрицы С, В и, А заданы, то функция Ay (t) и ее производные любого порядка являются известными функциями времени. Из последнего соотношения при t = О находим.

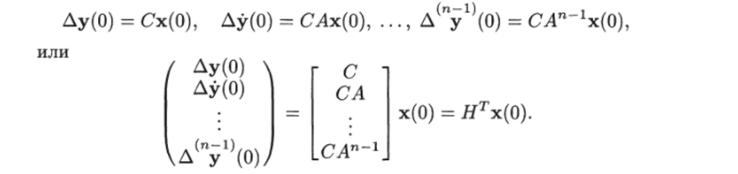
же выходной вектор у^($):

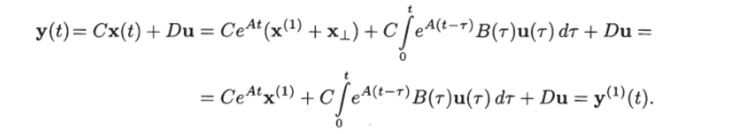
Полученное векторное уравнение с п неизвестными х,-(0) (г = = 1,2,…, п) равносильно системе из пр уравнений. Так как ранг матрицы Н^т равен п, то среди уравнений этой системы имеется ровно п независимых уравнений. Выделив эти уравнения и решив их, определим искомый вектор х (0).

Наблюдаемость (восстанавливаемость) управляемой системы (1.19) полностью определяется матрицами, А и С. И наряду с наблюдаемостью управляемой системы используется понятие наблюдаемости пары (А, С).

Пара (А, С), где А — (п х п)-матрица и С — (р х п)-матрица, называется наблюдаемой или полностью наблюдаемой (восстанавливаемой), если матрица наблюдаемости, составленная из этой пары,.

имеет ранг п или, что-то же, управляемая система (1.19) вполне наблюдаема.

Наблюдаемость управляемой системы, как и управляемость, является внутренним свойством системы: оно не зависит от того, в какой системе координат записаны уравнения управляемой системы. Покажем это.

При неособом преобразовании 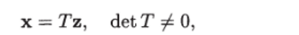уравнения управляемой системы (1.19) принимают вид где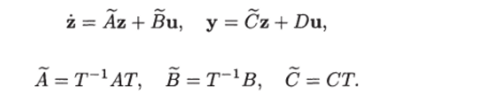

Как легко проверить, транспонированная матрица наблюдаемости преобразованной системы имеет вид.

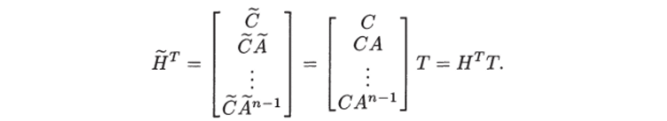
Так как матрица Т неособая и ее ранг равен п, ранг матрицы наблюдаемости Н^т совпадает с рангом матрицы Я^т.

Пример 1.5. Исследовать наблюдаемость управляемой системы.

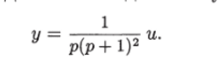
Решение. Преобразуем данное уравнение в нормальную форму. Его можно записать в виде.

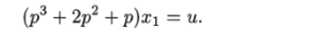
Положив у = a? i, у = ?2И2/ = Яз, получим.

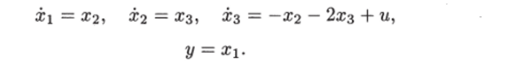
Матрицы Л, С и их произведения имеют вид.

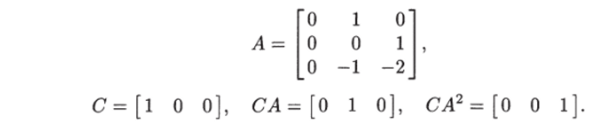
Отсюда для транспонированной матрицы наблюдаемости получаем.

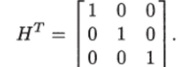
Ранг этой матрицы равен 3, так как det Н^т = 1⁰. Следовательно, рассматриваемая система вполне наблюдаема.