Последовательная и параллельная схемы замещения пассивного двухполюсника

Два линейных пассивных двухполюсника с одинаковыми комплексными сопротивлениями (комплексными проводимостями) эквивалентны, так как при замене одного из них другим токи и напряжения внешних выводов, соединяющих двухполюсники с остальной частью цепи, не изменятся. Следовательно, условием эквивалентности линейных пассивных двухполюсников является равенство их комплексных сопротивлений (проводимостей).

Комплексное сопротивление любого пассивного двухполюсника Z = г +jx можно представить как сумму комплексных сопротивлений двух последовательно включенных двухполюсников. Комплексное сопротивление одного из них имеет чисто резистивный Z_a = г, а другого Z_p =jx — чисто реактивный характер. Комплексную проводимость этого двухполюсника Y = 1/Z = g + jb можно рассматривать как комплексную проводимость цепи из двух параллельно соединенных элементов с проводимостями У_г = g и У_р =jb. Поэтому произвольному линейному пассивному двухполюснику, находящемуся под гармоническим воздействием, можно поставить в соответствие две схемы замещения — последовательную (рис. 2.42, а) и параллельную (рис. 2.43, а), причем каждая из них содержит один реактивный элемент и один элемент, входное сопротивление которого имеет чисто резистивный характер.

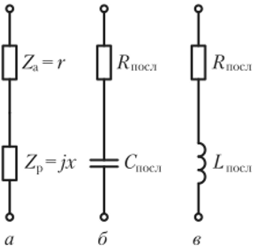
Рис. 2.42. Последовательные схемы замещения пассивного двухполюсника.

В общем случае вещественные г, g и мнимые х, b составляющие комплексного входного сопротивления и комплексной входной проводимости пассивного двухполюсника являются сложными функциями частоты: г = г (со), х = х (со), g = g (со), b = Ь (со). При изменении частоты вещественные составляющие г и g могут изменяться только по абсолютному значению, а мнимые составляющие х и b — как по абсолютному значению, так и по знаку. При фиксированном значении угловой частоты со = сох вещественные и мнимые составляющие входных сопротивления и проводимости двухполюсника, а следовательно, Z_a, Z_p, а также F_a, F_p элементов последовательной и параллельной схем замещения принимают определенные значения: Z_a = r (coi), Z_p= jx (сщ), F_a ⁼ g (coj), F_p = jb ((o_t). Постоянное вещественное число Z_a = r ((Dj) можно рассматривать как комплексное сопротивление резистивного элемента, входящего в последовательную схему замещения двухполюсника (рис. 2.42, б, в):

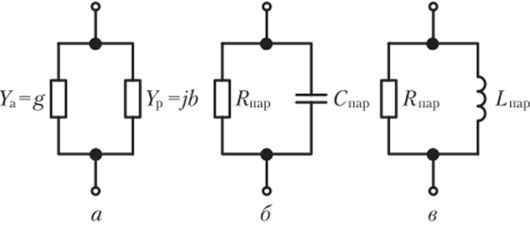
Рис. 2.43. Параллельные схемы замещения пассивного двухполюсника.

Мнимое число Z_p = jx (coj) в зависимости от знака x (g)i) можно рассматривать либо как комплексное сопротивление емкости (x (coj) < 0).

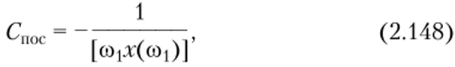
либо как комплексное сопротивление индуктивности (х ((о,) > 0).

входящих в эту же схему замещения.

Параллельная схема замещения двухполюсника (рис. 2.43, б, в) содержит сопротивление.

и либо емкость (Ь (а>_{) > 0).

либо индуктивность ^< 0)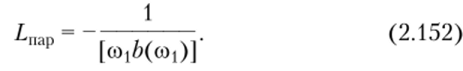

В частном случае, когда входное сопротивление двухполюсника имеет чисто резистивный или чисто реактивный характер, обе схемы замещения вырождаются в одну, содержащую единственный идеализированный пассивный элемент (сопротивление, емкость или индуктивность).

Таким образом, при фиксированном значении частоты внешнего воздействия каждому линейному пассивному двухполюснику независимо от числа входящих в него элементов и способа их соединения можно поставить в соответствие эквивалентную схему, содержащую не более двух идеализированных пассивных элементов. Разумеется, такое преобразование будет эквивалентным только при со = соу. Изменение частоты внешнего воздействия может вызывать изменение не только значений параметров элементов последовательной и параллельной схем замещения двухполюсника, но и характера соответствующих реактивных элементов.

Последовательная и параллельная цени, схемы которых приведены на рис. 2.42, а и 2.43, а, обладают одинаковыми комплексными сопротивлениями (проводимостями) и поэтому являются эквивалентными. Выбор той или иной цепи и соответственно той или иной схемы замещения двухполюсника при заданной частоте внешнего воздействия производится исходя только из удобства последующего анализа.

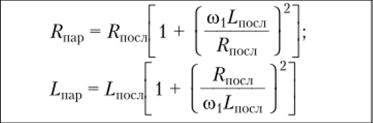
При необходимости последовательная и параллельная схемы замещения двухполюсника могут быть преобразованы одна в другую. Соотношения между параметрами их элементов однозначно устанавливаются с помощью выражений (2.52)—(2.55) и (2.147)—(2.152). Анализ этих выражений показывает, что при взаимных ?7реобразованиях последовательной и параллельной схем характер реактивного элемента, входящего в схему замещения, не изменяется (табл. 2.1).

Выражения, приведенные в таблице, можно использовать для взаимных преобразований произвольных участков цепей с параллельным и последовательным включением элементов. Например, при заданной частоте внешнего воздей;

Таблица 2.1

Формулы для взаимного преобразования параллельной и последовательной схем замещения пассивного двухполюсника

Параметры исходной цепи.	Параметры преобразованной цепи.
^посл" ^посл.
^посл" Аиосл.
^пар* ^пар
-*Miap> ^пар

ствия (0 = 0)! участок цепи, представляющий собой последовательное соединение сопротивления и емкости Сможет быть заменен эквивалентным участком цепи с параллельно включенными сопротивлением /?₂ и емкостью С₂. Несмотря на то что в данном случае параметры элементов исходной цепи не являются функциями частоты, параметры элементов преобразованной цепи /?₂, С₂ зависят от частоты внешнего воздействия. При этом изменение частоты внешнего воздействия приводит только к изменению значений параметров элементов преобразованной цепи; характер реактивных элементов в данном случае не меняется.

Пример 2.16. Построим последовательную и параллельную схемы замещения последовательной RLC-цепи (см. пример 2.4) при частоте внешнего воздействия со = coj = 2,5- Hr рад/с.

Комплексное сопротивление цепи при со = С0[ имеет резистивио-емкост!I ый характер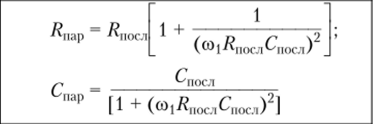

поэтому последовательная и параллельная схемы замещения цепи на данной частоте содержат сопротивление и емкость (см. рис. 2.42, 6 и 2.43, в). Параметры элементов последовательной схемы замещения в соответствии с выражениями (2.147) (2.148) /?_посл = r (coi) = 100 Ом; С_посл= -l/[coi.r (coi)] = 666,7 пФ.

Параметры элементов параллельной схемы замещения найдем, используя формулы, приведенные в табл. 2.1: