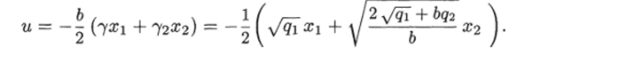Синтез стабилизирующего закона управления при линейном относительно состояния уравнении объекта

Преобразуя первое слагаемое в соответствии с тождеством 2хТСх = хт (С + Ст) х, последнее равенство можно представить в виде Если пара (А, В) вполне управляема и Л > 0, то это матричное уравнение разрешимо, и его решением будет положительно определенная матрица Г. Линейный объект. Функция y?(u,?) = и удовлетворяет последнему условию (8.48). Следовательно, стабилизирующий закон управления объекта… Читать ещё >
Синтез стабилизирующего закона управления при линейном относительно состояния уравнении объекта (реферат, курсовая, диплом, контрольная)
Чтобы воспользоваться алгоритмом управления (8.44), необходимо задать одну из двух положительно определенных функций, w (x,?) или К (х, t), а вторую определить исходя из уравнения (8.45). Однако в общем случае, когда объект описывается уравнением (8.34а), какихлибо рекомендаций по выбору этих функций нет. Задача синтеза намного упрощается, когда управляемая система описывается линейным относительно вектора состояния уравнением.
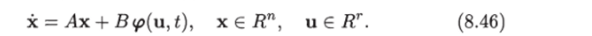
Здесь А, В — постоянные (п х п)-матрица и (п х г)-матрица, пара (А, В) управляема, т. е. ранг матрицы управляемости равен п:
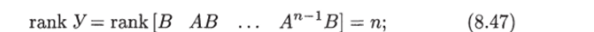
нелинейная функция.
удовлетворяет условию.

Линейный объект. Функция y?(u,?) = и удовлетворяет последнему условию (8.48). Следовательно, стабилизирующий закон управления объекта (8.46) будет стабилизирующим законом управления и для объекта, который описывается линейным уравнением.
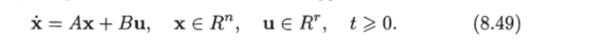
Однако найдем сначала стабилизирующие законы управления для более простого объекта (8.49), а затем вернемся к исходному объекту (8.46).
В случае объекта (8.49) g (x, t) = Ах, и уравнение (8.45) принима.

ет вид Если принять.

то последнему уравнению будет удовлетворять квадратичная форма V = хтГх. Действительно, так как.

то оно принимает вид.

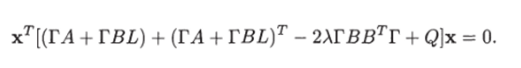
Преобразуя первое слагаемое в соответствии с тождеством 2хТСх = хт(С + Ст)х, последнее равенство можно представить в виде Если пара (А, В) вполне управляема и Л > 0, то это матричное уравнение разрешимо, и его решением будет положительно определенная матрица Г [59].
Закон управления (8.44) при выборе функции р (х, t) в соответствии с (8.42) принимает вид.
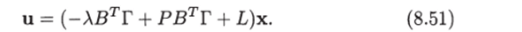
Здесь Р — произвольная кососимметрическая матрица.

Это равенство будет выполнено тождественно, если имеет место равенство.
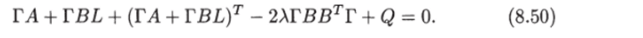
При 1 = 0, р = 0 закон управления (8.51) и уравнение (8.50) принимают вид.
Нелинейный объект. Закон управления (8.52), стабилизирующий линейный объект (8.49), является стабилизирующим законом управления и для нелинейного объекта (8.46).
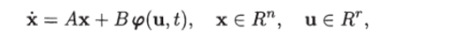
т. е. замкнутая система (8.46), (8.52) асимптотически устойчива.
Чтобы доказать это, достаточно показать, что положительно определенная квадратичная форма V = хТГх является функцией Ляпунова для системы (8.46), (8.52), удовлетворяющей теореме об асимптотической устойчивости.
Производная по времени этой квадратичной формы в силу уравнения (8.46) имеет вид.
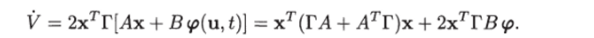
Прибавив и вычтя хг2АГВВтГх, получим.

Используя (8.526), это соотношение можно преобразовать к виду или 
Отсюда, учитывая закон управления (8.52а), получаем.
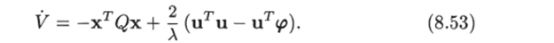
В силу условия (8.48) второе слагаемое в правой части является неположительным. Следовательно, производная V является отрицательно определенной функцией.
Пример 8.10. Определить стабилизирующий закон управления для объекта 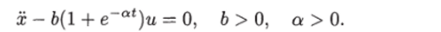
Решение. В нормальной форме уравнение объекта принимает вид В данном случае имеем (см. (8.46)) 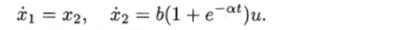
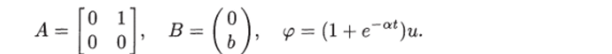
Функция у? удовлетворяет условию (8.48). Примем Л = ½ и матрицы Q и Г представим следующим образом:

Найдем произведения матриц, необходимые для записи соотношений (8.52) 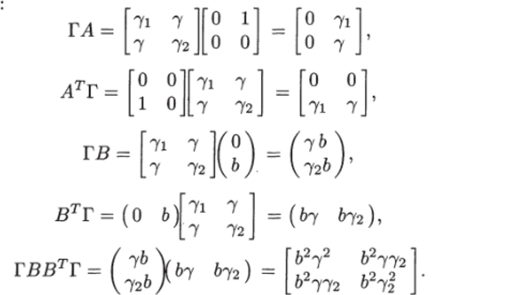
Уравнение 18.5261 ппинимает вил 
В скалярной форме оно записывается в виде.
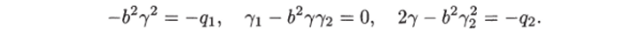
Чтобы матрица Г была положительно определенной, по критерию Сильвестра решение этой системы должно удовлетворять условию 7i > 0, 7i72 — 72 > 0. Таким решением является.

Закон управления (8.52а) принимает вид 264