Взаимная растворимость жидкостей

Когда две жидкости смешиваются только частично, тогда экспериментальные данные по их взаимным растворимостям могут быть использованы для определения коэффициентов активности во всем диапазоне составов гомогенных областей. Предположим, что растворимость (мольная доля) компонента 1 в компоненте 2.

равняется х_{, а компонента 2 в компоненте 1 соответственно.

*2 • Индекс s означает насыщение, а штрихами обозначены две жидкие фазы. Если и лг₂ известны при некоторой температуре Г, то можно определить коэффициенты активности для обоих компонентов в гомогенных областях О < Xj < х{ и 0 < x₂ < х₂ .

Для определения коэффициентов активности необходимо выбрать какое-либо термодинамически совместимое аналитическое выражение, которое связывает коэффициенты активности Yi и у2 с мольной долей х (см. раздел 1.3). Такое выражение содержит одну или более констант, характеризующих бинарную систему. Эти константы обычно зависят от температуры, хотя ее влияние часто невелико. Две такие константы можно определить из уравнений равновесия жидкость — жидкость, которые имеют вид:

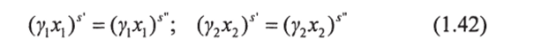
Предположим, что было выбрано двухкомпонентное выражение для мольной избыточной энергии Гиббса gf. Тогда (см. раздел 1.3).

где fufi — известные функции; А, В — неизвестные константы.

Константы Л и В могут быть найдены совместным решением уравнений (1.42) и (1.43) с использованием экспери;

С¹ с" .

ментальных значений х_х и х₂, а также уравнений материального баланса.

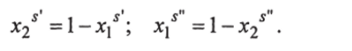
Расчет в принципе прост, хотя алгебраические преобразования могут потребовать некоторого труда (это зависит от сложности функций f и fi).

Для иллюстрации в табл. 1.12 представлены результаты для пяти бинарных водных систем. Индекс 2 относится к воде. Для расчетов использовались уравнения Ван-Лаара и двухпараметрическое уравнение Маргулеса (табл. 1.3). В табл. 1.12 даны расчетные значения коэффициентов активности при бесконечном разбавлении, которые находятся в простой связи с константами А и В (см. уравнения (1.37) и (1.38)).

Расчеты показывают, что результаты чувствительны к выбору выражения для мольной избыточной энергии Гиббса. При сравнении результатов расчета с экспериментальными данными по равновесию пар — жидкость уравнение Маргулеса дает плохие результаты, а уравнение Ван-Лаара — приемлемые, хотя и невысокой точности.

Расчеты подобного рода могут быть проведены и по трехпараметрическому уравнению для g^E, однако в этом случае третий параметр должен определяться независимо.

Вообще говоря, данные по взаимной растворимости позволяют находить только приближенные значения коэффициентов активности, хотя, конечно, лучше хоть такие расчеты, чем никаких. Их результаты чувствительны не только к выбору выражения для g^E, но даже и к малым ошибкам эксперимента по определению взаимной растворимости.

Таблица 1.12. Предельные коэффициенты активности, рассчитанные по значениям взаимных растворимостей в пяти бинарных водных системах.

лена.