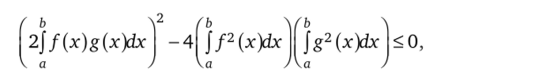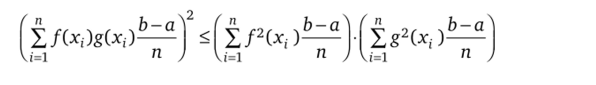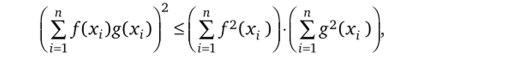Некоторые известные интегральные неравенства

Неравенство Коши — Буняковского

Рассмотрим неравенство Коши — Буняковского в интегральной форме (1859), являющееся аналогом известного числового неравенства Коши — Буняковского.

Теорема 2.3 (неравенство Коши — Буняковского в интегральной форме). Пусть функции/ug интегрируемы по Риману на отрезке [а, Ь]. Тогда справедливо неравенство

Доказательство. Из неравенства (f (x)-t g (x))² >0 (xe[a, b], teR) следует, что.

Левая часть последнего неравенства — квадратный трехчлен относительно t. Данное неравенство выполняется при всех t тогда и только тогда, когда дискриминант этого квадратного трехчлена неположителен, т. е.

откуда вытекает требуемое неравенство. Теорема доказана.

Замечание 2.4. Интегральное неравенство Коши — Буняковского можно было доказать иначе, а именно, как следствие соответствующего числового аналога. Рассмотрим и это доказательство.

Лемма 2.1 (неравенство Коши — Буняковского в числовой форме). Пусть а₁, а₂,…, а_п и Ь₁, Ь₂^—уК — произвольные неотрицательные числа. Тогда справедливо неравенство.

Доказательство. Очевидно, что Jab < ^{а +} ^ для любых неотрицатель;

а? №

?"? ib?

i=l i=l.

ных чисел а и Ъ. Положим в последнем неравенстве а = —^?—, Ь = —^!—.

и просуммируем по i от 1 до п. Получим откуда немедленно следует неравенство (2.5). Лемма 2.1 доказана.

Т1 П

Отметим, что в силу очевидного неравенства? ^аА ^Х1^аА1 утверж;

i=i i=i.

дение леммы справедливо для произвольных (необязательно неотрицательных) чисел a_h b_h i = 1,2,…, п.

Рассмотрим разбиение Т = отрезка [a, b] на п равных частей. Тогда неравенство (2.5) получается предельным переходом в неравенстве.

или эквивалентном неравенстве.

которое представляет собой неравенство Коши — Буняковского в числовой форме.