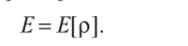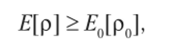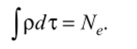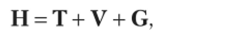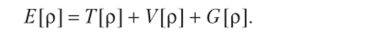Метод функционала электронной плотности

Теория функционала плотности (Density Functional Theory — DFT) для расчета энергии и других молекулярных свойств опирается не на волновую функцию, как это делается при решении уравнения Шрёдингера, а на электронное распределение.

Основные положения метода

В отличие от метода Хартри — Фока, где основным элементом теории является многоэлектронная волновая функция, в методе DFTтакими элементами являются электронная плотность и одноэлектронные орбитали — так называемые орбитали Кона — Шэма.

Современный метод функционала плотности основывается на следующей теореме Хоэнберга — Кона.

1. Энергия, волновая функция и другие молекулярные электронные свойства молекул, находящихся в невырожденном основном состоянии, однозначно определяются распределением электронной плотности. Это означает, что каждое свойство может быть записано как функционал электронной плотности, например энергия.

2. Для некоторой пробной (р) и точной (р₀) электронной плотности имеет место соотношение.

где Е₀ — точная энергия основного состояния.

Условие нормировки электронной плотности вытекает из того, что вся электронная плотность, интегрированная по всем пространственным координатам, должна равняться суммарному количеству электронов системы.

Система взаимодействующих электронов характеризуется гамильтонианом.

где Т, V и G — операторы кинетической энергии, потенциальной энергии притяжения электронов к ядрам и потенциальной энергии отталкивания электронов соответственно.

Если электронную плотность в конкретной точке пространства обозначить через р, то электрошшая энергия равна сумме соответствующих данным операторам функционалов.