Термы атомов. 
Квантовая механика и квантовая химия

Порядок расположения энергетических уровней атома {термов) с заданными значениями L и S по энергии основного состояния атома определяется эмпирическими правилами Хунда.

Наименьшей энергией обладает состояние с возможным наибольшим значением S. При одинаковой мультиплетности более стабильно состояние с максимальным значением L.

Для конфигураций, заполненных наполовину и менее, более стабилен терм с минимальным значением J (т.е. равно |L-S). Для конфигураций, заполненных более чем наполовину, более стабилен терм с максимальным J (т.е. равно L+S). Сказанное наглядно отражено на диаграмме (рис. 18.1), где N_e и N — количество соответственно электронов и орбиталей электронной подоболочки.

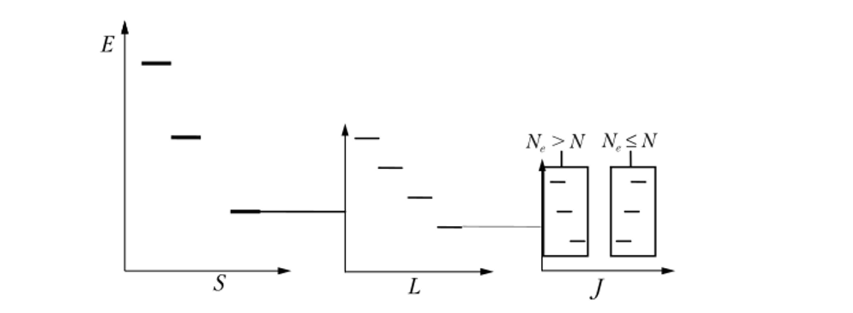
Рис. 18.1. Энергия терма и значения полных квантовых чисел многоэлектронной системы

Для определения термов рекомендуют пользоваться следующей последовательностью действий: записывается электронная конфигурация частично заполненных подоболочек атома; электроны распределяются по орбиталям так, чтобы в соответствии с правилами Хунда имели максимальные значения S и L; магнитные квантовые числа неспаренных электронов суммируются и дают магнитное квантовое число полного орбитального момента, которое и определяет величину квантового числа L; по числу неспаренных электронов определяется мультиплстность терма; наконец, находится квантовое число J.

Запишем спектроскопические обозначения состояний атомов некоторых элементов периодической системы.

Атом Н Is¹. Квантовые числа п = 1, / = 0, т = 0, s = ½.

Полное орбитальное квантовое число L = 0, полный спин S = ½, мультиплетность М = 2, квантовое число полного момента J = 0 + ½ = ½.

Состояние ²S, ₂.

Атом He Is². Квантовые числа и₁ = 1, 1_Х = 0, т_х = О, Sj = ½; п₂ = 1, /₂ = 0, т₂ = 0, s₂ = -½.

Тогда имеем L = 0, 5=0, M=1,J = 0 + 0 = 0.

Состояние ¹S₀.

Атом Li 1 s²2s^l: п_{ = 1,1_Х = 0, т_{ = 0, s_{ = ½; п₂ = 1, /₂ = О, т₂ = 0, s₂ = -½; А2₃ = 2, /₃ = 0, га₃ = 0, s₃ = 1 /2.

Конфигурация полностью занятой 1-й электронной оболочки, как у атома гелия, дает нулевые вклады в полные моменты L, S и J. Поэтому состояние атома в целом полностью определяется состоянием третьего электрона.

Поэтому можно записать Li …2s¹: п₃ = 2, /₃=0, т₃ = 0, s₃ =½; J= 0+ ½ = ½, М= 2−½ + 1 = 2.

В связи с этим все атомы с закрытыми внутренними оболочками и конфигурацией ns^{ будут иметь только одно основное состояние ²S_1/r

Атом Be ls²2s² или …2s². Как и у гелия, все атомы, с конфигурацией …ns¹ и имеющие полностью занятые электронные подоболочки, будут иметь основное состояние ^]S₀.

А том В ls²2s²pⁱ или …2s²p или, поскольку 25²-подоболочка полностью заполнена, основное состояние атома определяется только состоянием валентного p-электрона, т. е. конфигурацией В…2р Имеем.

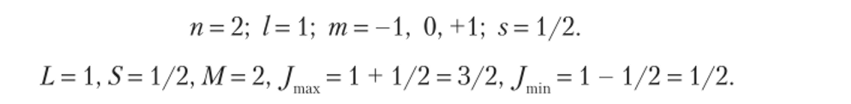
Подоболочка заполнена менее чем наполовину, поэтому для бора из возможных термов ²Р_{3 2} и ²Р, ₂ по третьему правилу Хунда более стабильным будет терм ²Р_½.

Атом С …2р². Термы основного состояния углерода рассмотрены выше. Найдем здесь все возможные термы атома углерода в написанной электронной конфигурации. Для электрона, находящегося на /7-подоболочке, возможно шесть микросостояний, определяемых возможными значениями квантового числа w = -1, 0, +1 и спинового числа s = +½, -½. Запишем возможные микросостояния двух электронов указанием комбинации т*т* магнитных квантовых чисел первого т* и второго т электронов. Используем надстрочный символ «+» для электрона со спином +½ и «-» — для электрона со спином -½. Например, микросостояние -1⁺1^_ указывает т_л = -1, s_x = +½, т₂ = +1, s₂ =.

= -½. Имеем следующие 36 состояний двух независимых электронов (табл. 18.1).

Таблица 18.1

Микросостояния конфигурации р²

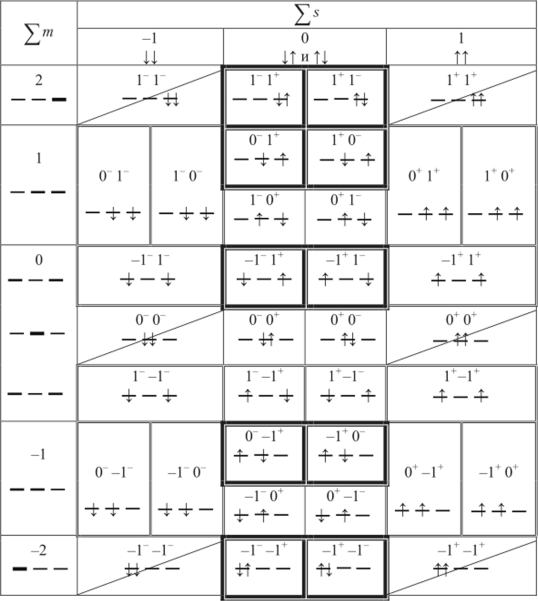
Из этих микросостояний получают систему термов. Для этого отбросим все микросостояния, противоречащие принципу Паули. В таблице они зачеркнуты. Из оставшихся микросостояний выбираем максимально возможное значение L-^m, равное 2. Значит, возможен терм D. Кроме того, S = 2^s = 0, следовательно, получаем терм 'D,. Для этого терма должны существовать микросостояния с изменяющимся ^ т от -2 до +2 (пять значений) и^s = 0. Последнее возможно в виде двух вариантов: 5 = +½−½ = 0 и 5 = -½ +.

+ ½ = 0. Всего таких микросостояний 5×2 = 10. Эти микросостояния в табл. 18.1 обведены полужирной рамкой.

После отделения микросостояний терма в строке ^т = 1 остались микросостояния ³Р₂ терма, которые обведены тонкой рамкой. В конечном счете остались микросостояния, относящиеся к терму ^lS₀.

Рассматривая конфигурации только с положительными значениями полного спинового момента (так как ориентацию оси 2 можно выбрать произвольно), из таблицы можно сделать вывод, что конфигурация углерода …р² 15-кратно вырождена. Поэтому в соответствии с правилами Хунда положение энергетических уровней атома углерода можно изобразить следующим образом (рис. 18.2):

Рис. 18.2. Энергетические уровни электронной конфигурации пр^2.

Атом N …2р Аналогичным образом получают, что для конфигурации пр³ существуют следующие термы: ²Р_{3 2}, -ГЛ.

5/2 ' °3/2 *.

Энергия термов рассчитывается через энергию микросостояний, составляющих термы. Было видно, что для двух эквивалентных р-электронов имеются три терма: ³Р, 'D, ^,S. Микросостояние 1⁺1″ принадлежит только терму ^!D, поэтому.

Микросостояние ГО* относится только к терму ³Р, поэтому.

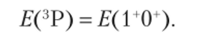
Для нахождения энергии терма 'S нужно учесть, что, например, 1=0иХ=0 В клетке вышеприведенной таблицы отвечают микросостояния сразу трех термов. Поэтому используют так называемое правило сумм

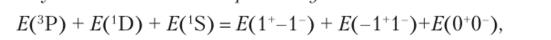
откуда с учетом уже известных энергий термов ¹D и ³Р можно найти энергию терма ‘S.

Возникает система термов для конкретной конфигурации из-за кулоновского взаимодействия между электронами, которое, как было ранее показано, определяется вкладами кулоновского (/) и обменного (К) интегралов. Причем последний интеграл имеет место только для электронов с параллельными спинами. Тогда энергия электростатического взаимодействия электронов и составляет энергию термов. Относительная энергия отдельного микросостояния при этом легко вычисляется, например:

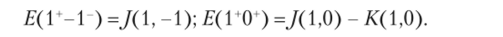
Интегралы,/ и К рассчитываются либо с помощью квантово-химических программ, либо через так называемые коэффициенты Кондона — Шортли и некоторые более простые интегралы. Последний вариант предусматривает использование водородоподобных функций.