Случайные события и действия над ними

Определим теперь, что будет пониматься иод случайными событиями. Начнем с примеров. Так, в эксперименте из примера 1.1 можно говорить о том, что номер извлеченного шара будет меньше или равен 3. Будем говорить, что это произойдет тогда и только тогда, когда эксперимент окончится одним из элементарных исходов coj, (c)2, 0)3. Таким образом, подмножество, А = {со₁₍ о>2, 0)3} множества П соответствует тому, что номер извлеченного шара < 3. Аналогично, подмножество В = {(со_с, СО;,), (ю_с, со_к)} множества Q из примера 1.2 соответствует тому, что первым будет извлечен синий шар.

Пусть теперь Q — произвольное пространство элементарных исходов. Случайными событиями будем называть подмножества А множества Q. Ясно, что событие А происходит тогда и только тогда, когда эксперимент оканчивается одним из элементарных исходов из А. Элементарные исходы из А будем называть благоприятствующими событию А элементарными исходами. Тот факт, что элементарный исход to благоприятствует событию А, т.с. принадлежит А, будем обозначать ш е А. Если со не принадлежит событию А, то будем обозначать со g А. Пусть, А и В произвольные события из Q, и пусть каждый элементарный исход со, благоприятствующий событию А, благоприятствует и событию В. Это означает, что из наступления события, А следует наступление события В, что будем обозначать, А с В или В з А. Если события, А и В состоят из одних и тех же элементарных исходов, то они называются равносшъными. Тот факт, что события, А и В равносильны, будем обозначать, А = В. Событие, соответствующее множеству С1, будем называть достоверным событием. Событие, не содержащее ни одного элементарного исхода, называется невозможным и обозначается 0. Через, А будем обозначать событие, состоящее из элементарных исходов, принадлежащих множеству Q и не принадлежащих А. Событие, А называется противоположным событию А. А происходит тогда и только тогда, когда не происходит событие А.

Операции, которые производятся над событиями, удобно иллюстрировать с помощью диаграмм Вениа, на которых множество Q. изображается в виде прямоугольника, а события в виде подмножеств множества О. Например, если событию, А соответствуют элементарные исходы (точки прямоугольника), лежащие внутри заштрихованной области.

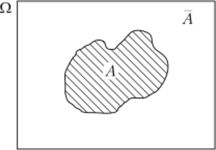
Рис. 1.8.

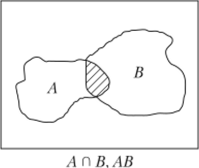
Рис. 1.9.

(рис. 1.8), то А содержит элементарные исходы, лежащие вне ее. Над событиями можно производить действия, аналогичные действиям над множествами. Пусть А и В — два события из пространства? Х Множество, состоящее из элементарных исходов, принадлежащих и событию Л, и событию В, образует событие А П В (или АВ), называемое пересечением (или произведением) событий А и В. Ясно, что событие АВ происходит тогда и только тогда, когда в результате эксперимента происходят и А, и В. На рис. 1.9 событию А и В соответствуют элементарные исходы, принадлежащие заштрихованной области.

Пример 1.8. Рабочий обслуживает два автоматических станка. Пусть события А и В состоят в том, что в течение интервала времени Т первый (соответственно второй) станок потребует внимания рабочего. Тогда событие, заключающееся в том, что оба станка потребуют внимания рабочего, С = АВ.

Пример 1.9. Рассмотрим задачу из примера 1.6, в. Пусть событие А заключается в том, что давление на опору X, 5 < d_x< 20, а событие В — давление на опору У, d_y > 3. Тогда Л Б графически представлено на рис. 1.10.

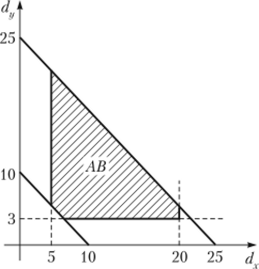
Рис. 1.10.

Объединением (суммой) двух событий А и В называется событие A U В (или А + В), содержащее элементарные исходы, которые принадлежат или событию А, или событию В, либо обоим одновременно. На рис. 1.11 событие Л U В изображено заштрихованной фигурой.

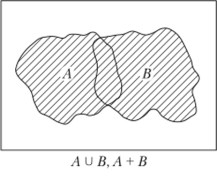
Рис. 1.11.

Пример 1.10. Если в примере 1.8 через D обозначить событие, при котором «по крайней мере один из двух станков потребует внимания рабочего», то D = A U В.

Пример 1.11. Объединение событий Л и В, определенных в примере 1.9, иллюстрируется рис. 1.12.

Рис. 1.12.

Понятия пересечения и объединения событий можно перенести на любое число событий. Пересечением (произведением) событий А_иА₂, A3,… называется событие, обозначаемое Л] П А₂ П Аз П … (или Л^Лз…), содержащее элементарные исходы, принадлежащие всем указанным событиям.

Событие Л1Л₂Л₃… происходит тогда и только тогда, когда в результате эксперимента происходят все события А, Л₂, Л₃,…

Пример 1.12. В электрическую цепь последовательно включены п приборов, поломка любого из которых приводит к ее разрыву. Пусть событие А, — прибор не вышел из строя, а событие В — по цепи идет ток. Тогда В = Л^.-.Л,.

В дальнейшем, для краткости, событие В, эквивалентное.

П

произведению событий АА₂.А_п, будем обозначать П Л,.

1=1.

Объединением событий А, А₂, … называется событие,.

П

обозначаемое U Л,-, содержащее элементарные исходы, ко- 1−1.

горые принадлежат хотя бы одному из событий А, А->…

Пример 1.13. Если событию Л благоприятствуют только исхо.

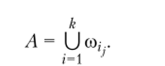
ды со,-, со,₂,…, со,-, то События А и В называются несовместными (непересекающимися), если А В = 0. События Л _ь А₂, … А^ называются попарно несовместными, если любые два из них несовместны. На рис. 1.13 приведен пример пяти попарно несовместных событий. Будем говорить, что события А_ь А₂,…, А^ образуют полную группу, если они попарно несовместны и объединение их — достоверное событие, т. е. A, Aj = 0 для.

П

любых i, j =1,2,…, п, i^j и ил, — = Q. Каждый элементарный.

/=1.

исход принадлежит одному и только одному событию из ПОЛНОЙ группы событий Л!, Л₂,…, Л".

На рис. 1.14 приведен пример шести событий, образующих полную группу событий.

Пример. 1.14. Для произвольного события Л, события Л и Л образуют полную группу из двух событий.

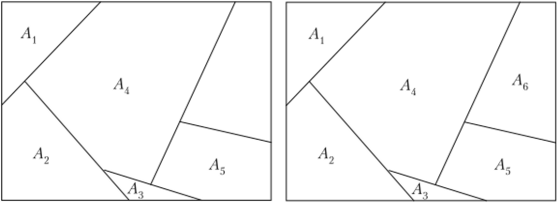
Рис. 1.14.

Рис. 1.13

Разностью событий А и В называется событие АВ, содержащее элементарные исходы, принадлежащие событию А и не принадлежащие событию В (рис. 1.15).

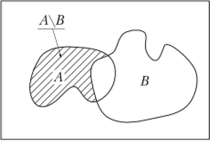
Рис. 1.15.

Введенные операции объединения и пересечения обладают переместительным, сочетательным свойствами и связаны распределительным законом, т. е. если А, В и С — любые события из пространства Q, то они обладают следующими свойствами:

.А U В = В U А;

• 2. АВ = ВА;
• 3. (A U В) U С = А и (В и су,
• 4. (АВ)С = А (ВС);
• 5. А (В U С) = АВ U АС.

Свойства I—4 непосредственно следуют из определения операций объединения и пересечения. Докажем свойство 5. Пусть элементарное событие со е Л (В и С'). По определению пересечения со е А и со е В и С. Таким образом со е А и со е В, либо со е А и со е С. Если со е АВ, то со е (АВ) и (АС), аналогично если со е А С, то со е (АВ) и (АС), т. е. доказано, что А (В U С) с (АВ) U (АС).

Точно также можно получит!) обратное включение, откуда будет следовать свойство 5. Приведенное доказательство можно кратко записать в следующем виде: со е А (В U С) тогда и только тогда, если со е А и (со е В или оз е С) (со е А и со е В) или (со е А и со е С) со е (АВ) U (АС).

Пример 1.15. Пусть Ли В — произвольные события из пространства Q. Тогда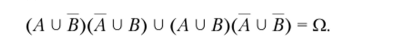

Доказательство. На основании свойства 5 имеем.

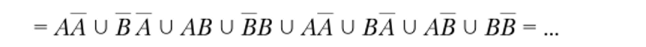
так как АЛ = 0 и В В = 0, и в соответствии со свойствами 2, 3 и 5 получаем.

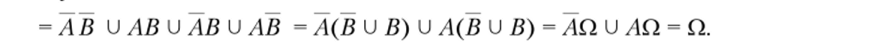
Пусть А_ь А₂, Аь произвольные события из пространства Q, то справедливо.

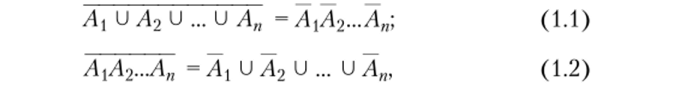
называемыми равенствами де Моргана.

Доказательство.

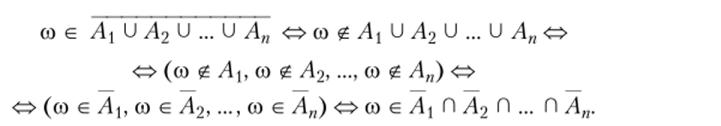
Проведенные выкладки показывают, что события, стоящие в левой и правой частях равенства (1.1), содержат одни и те же элементарные исходы, что и доказывает его справедливость. Равенство (1.2) доказывается аналогично [1, 2|.

Пример 1.16. В электрическую цепь включены три выключателя по схеме, указанной на рис. 1.16.

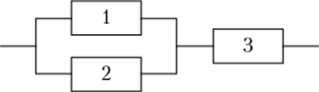
Рис. 1.16.

Рассмотрим следующие события:

Aj — включен выключатель i, i = 1, 2,3,.

В — по цепи идет ток.

Событие В можно представить в виде_Л = (А U А₂)А3. Противоположным к событию В будет событие В = «по цепи не идет ток». На основании правил дс Моргана можем написать.