Лекция №7, 8. Основы термодинамики. I, II и III начало термодинамики. 
Основы термодинамических расчетов

ЧАСТЬ 1

Термодинамика — наука, изучающая закономерности процессов, сопровождающихся взаимным превращением различных видов энергии (например, взаимные превращения тепла и работы). Объектом исследования в термодинамике являются только макроскопические системы. Термодинамический метод широко используется при исследовании самых разнообразных систем, в том числе геологических, металлургических, обогатительных и других. Этот метод позволяет определить количественные соотношения при превращении различных видов энергии, установить возможность протекания данного процесса и его глубину, т. е. равновесное состояние, до которого он может протекать в данных условиях.

I закон термодинамики

Термодинамику формируют три основных закона (или Начала). Первый закон термодинамики формулируется следующим образом: «Невозможно создать вечный двигатель первого рода (perpetuum mobile), т. е. такой, который производил бы работу без каких-либо затрат энергии». В раскрытии этого закона важную роль сыграли работы Гесса, Майера, Джоуля, Гельмгольца и др. Из этого закона следует принцип эквивалентности между теплотой и работой. Математическая запись данного закона выражается следующими уравнениями:

Q=U+W.

Q=dU+W.

Теплота, полученная системой (Q; Q), расходуется на работу (W; W), совершаемую системой и увеличение ее внутренней энергии (dU; U). Из этих трех энергетических величин только внутренняя энергия является функцией состояния системы и поэтому однозначно определяется параметрами системы (т.е. она является полным дифференциалом).

Теплота и работа представляют собой формы передачи энергии и поэтому являются функциями процессов. Они не являются полными дифференциалами.

Работа делится на совершаемую против внешних сил, т. е. работу расширения.

W_рас=PdV; W_рас=PdV; W=-VdP.

и работу, не связанную с изменением объема, условно называемую ''полезной'' W^/,.

W^/= W^/

Последняя может совершаться только при изменении состава системы.

Теплота зависит от теплоемкости системы © и температуры.

Q=Q=nC (T)dT.

Следует учитывать, что сама теплоемкость тоже зависит от температуры. Эта зависимость выражается уравнением (для случая, когда Т>Т₀=298К):

с (T)=a+bT+cT²+ c^/T^-2

Где: а, в, с, с^/ — коэффициенты, зависящие от природы и агрегатного состояния вещества, определены экспериментально и приведены в справочниках физико-химических величин. При использовании различных справочников результаты расчетов могут несколько отличаться.

В случае приближенных расчетов обычно достаточно использование выражения:

с (Т)=а+bТ Для газообразных веществ различают теплоемкости при постоянном объеме (с_v) и постоянном давлении (с_р). Связь между этими величинами определяет уравнение Майера:

с_p-с_v=R Если с_р, с_v — мольные, то R=const=8,31Дж/мольК с_p-с_v=R Если с_р, с_v — массовые, то R=R_удconst.

Например, для воздуха значение этой величины при н.у. равно 280 Дж/кгК Для идеальных газов теплоемкости постоянны и без учета энергии колебательного движения молекул (что справедливо при сравнительно невысоких температурах) равны:

• -для одноатомных молекул с_V=R3/2;
• -для двухатомных и линейных многоатомных молекул

с_V=R5/2;

-для нелинейных трехатомных и многоатомных молекул сV=3R.

Используя соотношение между теплоемкостями при постоянном давлении и постоянном объеме, выражают следующую величину показателя адиабаты:

=с_P/с_V

значение которого для идеального газа зависит только от числа атомов в молекуле газа. Для теплоемкостей можно использовать и такие выражения как:

с_P=R/(-1).

с_v=R/(-1).

для одноатомных газов =5/3=1,67.

для двухатомных газов =7/5=1,40.

для трехатомных газов =9/7=1,30.

Для жидких и твердых веществ теплоемкости с_р и с_V близки по величине:

с_р с_V

Для систем, не совершающих полезной работы (W^/=0), первый закон термодинамики принимает вид:

Q=dU+PdV.

при V=const Q_v=dU, Q_v=U.

при V=const Q_P=dU+PdV=d (U+PV).

Величина Н=U+PV называется энтальпией (или теплосодержанием системы). Энтальпия, подобно внутренней энергии, является функцией состояния системы и определяется ее параметрами:

Q_p=dH, Q_P=H.

Закон Гесса. Тепловые эффекты химических реакций

Тепловым эффектом называется количество выделенной или поглощенной теплоты при следующих условиях: система совершает только работу расширения, объем или давление остаются постоянными, температуры исходных и конечных веществ одинаковы, реакция протекает практически до конца.

Для расчета тепловых эффектов различных процессов, (в том числе и состоящих из нескольких этапов) в термодинамике применяют закона Гесса (установлен экспериментально Г. И. Гессом), который формулируется следующим образом: «Тепловой эффект химической реакции не зависит от пути процесса, а определяется лишь состоянием исходных и конечных веществ, в ней участвующих». Тепловой эффект химической реакции равен разности сумм произведений энтальпий образования конечных и исходных веществ на стехиометрические коэффициенты в уравнении реакции.

_rH⁰₂₉₈=n_кон(_fH⁰₂₉₈)_кон-n_нач(_fH⁰₂₉₈)_нач

Для различных веществ при нормальных условиях (Р₀=101,3 кПа; Т₀=298К) энтальпии образования обозначаются как _fН⁰₂₉₈, кДж/моль и приводятся справочниках физико-химических величин.

Для реальных систем закон Гесса используют при вычислении общего количества теплоты, необходимого для нагревания (или выделяющегося при охлаждении) любой системы от Т₁ до Т₂ при Р=соnst, где Т₁ Т₀:

Q_p=nс_p(T)dT.

Q_p=H=n[a (T-T₀)+b/2(T²-T²₀)+c/3(T³-T³₀)+c^/(1/T₀-1/T)+d/4(T⁴-T⁴₀)].

Закон Кирхгофа. Зависимость теплового эффекта химической реакции от температуры

Тепловой эффект процесса зависит от температуры. Эта зависимость определяется законом Кирхгофа, который формулируется следующим образом: «Частная производная от теплового эффекта по температуре равна разности теплоемкости системы в конечном и исходном состояниях». Для процессов, протекающих при постоянном давлении, этот закон выражается уравнением:

dQ_p/dT=d (_rH)/dT=(nC_p)_кон-(nC_p)_исх=_rC_p

Закон Кирхгофа справедлив для любых процессов при условии, что W^/=0, т. е. W=W_расш. Для приближенных расчетов: Q_p=_rH⁰₂₉₈+_ra (T-298)-(T²-298²)_rb/2. Где:

_ra=(na)_кон-(na)_исх.; _rb=(nb)_кон.-(nb)_исх..

ЧАСТЬ 2

II закон термодинамики. Теорема Карно-Клаузиуса

Задачей второго закона термодинамики является определение условий, в которых возможно протекание самопроизвольных процессов, и условий, при которых наступает равновесие.

Коэффициент полезного действия (кпд) тепловой машины, работающей по квазистатическому циклу Карно, не зависит от природы рабочего тела, а определяется только интервалом температур, в котором совершается работа. Справедливость этой посылки в термодинамике доказывает теорема Карно-Клаузиуса, являющаяся одной из формулировок II закона термодинамики:

где: Q₁ — теплота, сообщенная рабочему телу при температуре Т₁ от источника тепла; Q₁ — теплота, отданная телом при температуре Т₂ холодильнику.

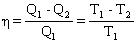
Основной формулировкой второго закона является формулировка Больцмана: «Все процессы в природе переводят систему из состояния менее вероятного в более вероятное».

В 1865 г. Клаузиус ввел новую функцию состояния S — энтропию, являющуюся мерой хаоса, неупорядоченности системы, которая принята в качестве меры вероятности: (математическая запись второго начала).

Второе начало имеет статистическую интерпретацию: S=k*ln (w) (формула Больцмана), где: k= - константа Больцмана, w — термодинамическая вероятность (или статистический вес) макросостояния.

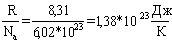
Величина, равная Q/T, называется приведенным теплом и является рассеянной теплотой, следовательно и энтропия характеризует рассеянность теплоты; размерность ее соответствует [Дж/мольК]. В изолированной системе (Q=0) приращение энтропии при равновесии равно приведенному теплу, а в самопроизвольных процессах больше приведенной теплоты. Энтропия является функцией состояния системы и однозначно определяется ее параметрами.

III закон термодинамики. Теорема Нернста. Постулат Планка

Важное значение в раскрытии этого закона принадлежит работам Нернста и Ричардса. В частности, Нернст в 1906 г. в своей классической работе «О вычислении химического равновесия из термических данных» высказал гипотезу, суть которой эквивалентна следующему утверждению:

при Т0 S=0 и S=0. Важнейшим следствием этой гипотезы является то, что энтропия правильно сформированного (бездефектного) идеального кристалла при 0К равна 0. Этот постулат впервые сформулировал Планк в 1912 г. По сути, это и есть формулировка третьего начала (закона) термодинамики: lim_T0S=0; S_T=с (T)dT/T.

На основе этого закона разработаны современные методы вычислений изменения стандартной энергии Гиббса, а также констант равновесия при различных температурах.

Определение термодинамической вероятности осуществления процесса

Для определения термодинамической вероятности осуществления процесса используют понятие изобарно-изотермического потенциала или энергии Гиббса G=U+PV-TS=H-TS. Энергия Гиббса является функцией состояния системы и имеет размерность энергии (кДж). При постоянном давлении и температуре энергия Гиббса может служить признаком самопроизвольного процесса или наличия равновесия. Самопроизвольно происходят только процессы, ведущие к ее уменьшению, при равновесии она постоянна и минимальна по величине. Изменение энергии Гиббса определяют как: G=H—(TS), H_х.р.=n_кон(_fH⁰₂₉₈)_кон-n_нач(_fH⁰₂₉₈)_нач; S_х.р=(nS⁰₂₉₈)_кон-(nS⁰₂₉₈)_нач.

Если значение G>0, то процесс термодинамически мало вероятен, причем, чем более положительно значение G, тем менее вероятен этот процесс.

Если значение G=0, то система находится в равновесии.

Если G<0, то процесс термодинамически вероятен, причем, чем более отрицательно значение G, тем более вероятен этот процесс.

Энергия Гельмгольца

Величина F=U-TS является функцией состояния системы и носит название изохорно-изотермического потенциала или энергии Гельмгольца (размерность энергии (Дж)). При Т, Р=const энергия Гельмгольца может служить признаком наличия равновесия или самопроизвольности процессов. При равновесии она постоянна и минимальна по величине. Самопроизвольно могут протекать только процессы, которые приводят к ее убыли.

Расчет энергетических величин и выражения первого закона термодинамики для предельных процессов идеального газа