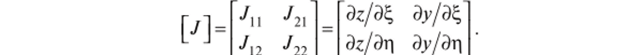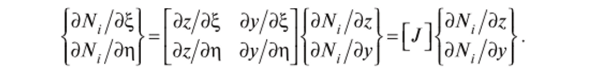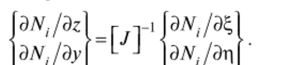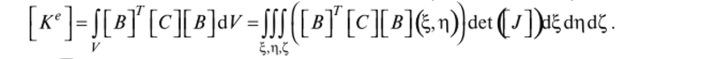Расчет коэффициентов жесткости

Входящие в уравнение (23.11) производные функций формы dNJdz и dNJdy, связанные с применением дифференциального оператора Коши D, невозможно вычислить без учета искажения реального пространства (в координатах z и у) по отношению к исходному, определяемому в естественной системе координат 5 и г| (см. рис. 23.13). В естественной системе прямоугольник не искажается никогда.

Для дальнейших преобразований нужно связать декартовы и естественные координаты формулами видах = /(§) или? = g (x).

или после обращения последнего выражения Величина dx/d? = |У| называется матрицей Якоби для одномерной задачи. Для двумерной задачи матрица Якоби имеет вид.

Тогда производные функций формы.

После обращения матрицы Якоби имеем.

Для составления элементов обратной матрицы Якоби используют численное интегрирование. Матрицу жесткости элемента можно определить путем численного интегрирования способом Гаусса—Лежандра, требующим меньшего количества точек интегрирования, чем другие способы.

Произведем замену переменной в выражении (23.11). Для малого элемента объема dV= dxdydz = |det[y]d^dpd^|. Тогда.

При численном интегрировании вместо интеграла вычисляют сумму значений по всем т узловым точкам с учетом весовых коэффициентов W. Естественные координаты точек интегрирования и весовые значения в этих точках задаются алгоритмом способа Гаусса—Лежандра в зависимости от числа точек интегрирования: