Группы. 
Дискретный анализ. 
Основы высшей алгебры

Определение и простейшие свойства

Абстрактная современная алгебра отличается от школьной тем, что в ней рассматриваются произвольные операции, удовлетворяющие заданным свойствам (аксиомам).

Мы будем рассматривать только бинарные операции, когда операция применяется к двум элементам. Говорят, что на множестве М определена бинарная алгебрамчсская операция *, если для всяких двух его элементов а и b однозначно определен элемент с = а * 6, называемый произведением элементов а и b (порядок операндов важен!). Примерами таких операций могут служить обычные операции сложения, вычитания или умножения на множестве действительных (или комплексных) чисел, операция умножения на множестве квадратных матриц данного порядка, операция композиции на множестве перестановок из п элементов, операция векторного умножения на множестве векторов трехмерного пространства.

Сам термин «произведение» подсказывает, что результат бинарной операции, примененной к элементам а и Ь, обозначается обычно а-b или даже ab. Это мультипликативная запись. Иногда используется аддитивная запись а + 6, особенно в тех случаях, когда на одном множестве рассматриваются сразу две операции. Когда используется аддитивная запись, результат операции обычно называется сулимой.

В общем случае операция применяется к упорядоченному набору из п элементов множества М (и называется тогда n-арной). По нас такой общий случай интересовать не будет.

По определению алгебраическая операция отличается тем, что ее результат не выводит из множества Л/ (говорят также, что М замкнуто относительно определенной на нём алгебраической операции). Этим алгебра принципиально отличается от математического анализа. В математическом анализе есть операции, которые выводят из множества. Например, операция нахождения производной непрерывной функции вовсе не обязательно дает непрерывную функцию. В алгебре такое исключено.

Рассмотрим несколько примеров алгебраических аксиом и задаваемых ими алгебраических структур.

Полугруппы. Имеется единственная аксиома а • (Ь • с) = = (а • Ь) • с. Такое свойство называется ассоциативностью. Множество с одной операцией, от которой требуется только ассоциативность и ничего больше, называется полугруппой. Мы ими заниматься не будем. Полугруппы встречаются довольно часто. Например, они важны для одной из современных математических теорий — так называемой теории автоматов.

Пример 1.1. Пусть А — конечное множество. Словом в алфавите А называется конечная последовательность элементов А. Множество слов в алфавите А обозначается А*. Для слов определена операция конкатенации: дописывание одного слова вслед за другим. Например, конкатенация аа и ЬЬ дает aabb. Множество слов с операцией конкатенации образует полугруппу. Действительно, результат конкатенации слов гг, v, w в каждом из двух случаев (uv)w и u (vw) — это слово, которое получается последовательным выписыванием символов слова гг, за которыми следуют символы слова V, за которыми следуют символы слова w.

Пример 1.2. Отоб]Х1Э1сепие множества X в множество Y ставит в соответствие каждому элементу множества X некоторый элемент множества У (можно считать Смпова «отображение» и «функция» синонимами). Обычно отображение / множества X в множество Y обозначается как /: X —> У, а записи.

/: х у и f (x) = у означают, что отображение / ставит в соответствие элементу х элемент у (у называется образом х). Если для каждого элемента у из множества Y существует хотя бы один элемент х из множества X такой, что f: х у (т в этом случае называется прообразом у), то отображение / называется отображением на множество Y.

На отображениях множества X в себя определена операция композиции (последовательного выполнения). Если f, g два отображения, то их композиция F = / о у задается формулой F (x) = f (g (x)). Отображения множества в себя с операцией композиции также образуют полугруппу:

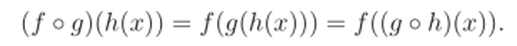
Обратите внимание, что в обоих примерах порядок операндов существенен.

Моноиды. Следующая алгебраическая структура — это множество с такой операцией, для которой кроме ассоциативности требуется еще наличие единицы, т. е. такого элемента, произведение с которым слева и справа оставляет любой другой элемент неизменным. Дополнительно мы потребуем, чтобы единичный элемент был единственным. Итак, имеем две аксиомы:

Ml: х? (у ‘ z) = (х? у) • z (ассоциативность);

М2: (аксиома единицы) существует единственный единичный элемент е такой, что для любого х выполняется е • х = = х? е = х.

Множество с ассоциативной и обладающей единицей операцией называется моноидом.

Рассмотренные выше примеры являются не только полугруппами, но и моноидами. В множестве слов единичным элементом относительно конкатенации является пустое слово (последовательность длины 0). В множестве отображений единичным элементом относительно композиции является тождественное отображение: id: х i-> х.

Замечание 1.3. Поскольку результат операции, вообще говоря, зависит от порядка операндов, иногда бывают нужны.

левые и правые единицы. Элемент е называется левой единицей, если для любого х выполнено ех = х. Аналогично, для правой единицы выполняется тождество хе = х.

Группы. Группа G = (М, *) — это такая пара из множества М и бинарной операции * на этом множестве, что выполняются следующие свойства (аксиомы группы):

G1: (ж * у) * z = х * (у * z) (ассоциативность);

G2: (аксиома единицы) существует единственный единичный элемент е такой, что для любого х выполняется е * х = = х * е = х

G3: для любого элемента х существует ровно один обратный элемент, т. е. такой элемент у, для которого у*х = х*у = = е (обратный элемент обозначается т^-1).

Группы с добавленным свойством коммутативности операции а*Ь = Ь*а называются коммутативными или абелевыми (по имени норвежского математика Абеля, который их изучал) .

При использовании мультипликативной записи х • у или ху единичный элемент группы традиционно называется единицей и обозначается е или 1. При аддитивной записи единичный элемент называется нулем и обозначается 0. Вместо термина «обратный» при аддитивной записи используется термин «противоположный». Противоположный к элементу у обозначается —у. Аддитивная запись обычно (но далеко нс всегда) используется для обозначения коммутативных операций.

Группа называется конечной, если в ней (а точнее — во множестве М) конечное число элементов, которое называется порядком группы.

Посмотрим на простейшие формальные следствия из групповых аксиом.

Первая аксиома группы означает независимость результата применения нескольких операций от расстановки скобок. По индукции можно распространить ее на сколь угодно длинные выражения. Другими словами, если есть конечная последовательность элементов группы ai, a2,…, a_n, то имеется однозначно определенный элемент группы.

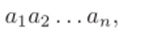
который нс зависит от того, в каком порядке расставлены скобки в этом выражении. Докажем это утверждение формально.

Будем доказывать индукцией, но числу сомножителей п, что при любой расстановке скобок произведение элементов а,…, а_п равно а (аг (… а_п)…). Основание индукции п = = 3 — это аксиома ассоциативности. Пусть утверждение доказано для произведений п элементов. Рассмотрим произведение (п+ 1)-го элемента. Оно имеет вид L? R, где в L и R элементов не больше п. Поэтому по предположению индукции L = а-Ь а L • R = (а? V) • R = а • (V • R). В V • R всего п элементов, так что можно еще раз применить предположение индукции и вывести справедливость доказываемого утверждения для произведений (п + 1)-го элемента.

Вторая и третья групповые аксиомы очень важны, потому что позволяют решать уравнения простейшего вида ах = b и ха = b:

(знаком обозначается равносильность утверждений).

Решения уравнений указанного вида в числах проходят в младших классах школы и дальнейшая школьная алгебра на них опирается. Если выполнены групповые аксиомы в какойнибудь более сложной ситуации (скажем, для движений пространства), то некоторые привычные равенства останутся справедливыми. Обычно проверять групповые аксиомы проще, чем проверять разрешимость линейных уравнений (чтобы это почувствовать, попробуйте решить уравнение ах = 6, где а — поворот вокруг оси z на 90° против часовой стрелки, b — поворот вокруг оси х на 90° по часовой стрелке).

Очень важно свойство сократимости: если взять два неравных элемента группы а ф Ь и умножить их на один и тот же элемент с, то снова получатся неравные элементы: ас ф Ьс. Это совершенно очевидно: если ас = Ьс, то и асс~¹ = Ьсс^-1, поэтому.

a = b. Аналогичное свойство выполняется и для умножения слева.

В качестве еще одного примера использования групповых аксиом проверим полезное равенство (ab)^-1 = Ь~¹а~¹, которое выражает обратный к ab элемент группы через обратные к а и Ь. Имеем.

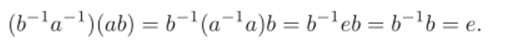
Здесь первое равенство получается после двух применений аксиомы ассоциативности, второе следует из определения обратного, третье — из аксиомы единицы, последнее — опять из определения обратного. Равенство (а6)(6^-1а^-1) = е проверяется аналогично.

Свойство сократимости облегчает перечисление небольших групп. Операцию в конечной группе естественно задавать таблицей, строки которой индексированы первыми операндами¹), столбцы — вторыми операндами, а в каждой клетке записан результат применения операции. Такая таблица называется таблицей Кэли (или таблицей умножения). Свойство сократимости означает, что в каждую строку и в каждый столбец таблицы Кэли каждый элемент группы входит нс более одного раза. А поскольку число строк и число столбцов таблицы равно числу элементов группы, то можно утверждать, что каждый элемент группы входит в каждую строку и каждый столбец ровно один раз.

Для группы из двух элементов таблица будет выглядеть так:

Три клетки заполняются, но аксиоме единицы:

С учетом свойства сократимости в четвертую клетку можно.

^Разумеется, чтобы записать таблицу на бумаге, нужно приписать всем элементам группы какие-то имена (символы).

поставить только е. Можно проверить, что таблица.

задает группу. Значит, существует единственная группа из двух элементов. Единственность здесь нельзя понимать буквально. Реализация группы может быть очень сложной: придавая разный смысл элементам е, а и групповой операции, можно получать содержательно разные примеры. Один из самых употребительных примеров группы второго порядка — множество чисел { — 1, +1} относительно операции умножения.

Аналогичный анализ можно проделать и для групп с тремя элементами. В этом случае также есть только одна группа.

Аксиома единицы оставляет незаполненными четыре клетки в таблице Кэли группы из трех элементов:

В центральной клетке не может стоять а. Если в ней стоит е, то приходим к противоречию со свойством сократимости: в третьем столбце второй строки должно стоять Ь, но в третьем столбце b уже есть. Получаем единственную возможность.

Обратите внимание, что заполненные части первой строки и первого столбца таблицы Кэли совпадают с первой строкой и первым столбцом той части таблицы, которая выделена линиями (единичный элемент стоит первым). В дальнейшем при задании группы таблицей Кэли мы будем придерживаться этого соглашения — единичный элемент стоит первым — и будем опускать ту часть таблицы, которая лежит слева и сверху от линий.

Классическая реализация группы из двух элементов имеет вид: е = 0, а = 1, групповая операция — сложение, но модулю 2 (суммируем и берем остаток от деления на 2). Аналогично для группы из трех элементов: е = О, а = 1,6 = 2, операция — сложение по модулю 3. Примеры групп из четырех, пяти и т. д. элементов получаются точно так же.

Из этих примеров можно увидеть, что для любого натурального п имеется хотя бы одна группа с п элементами. Сколько есть существенно разных групп с п элементами? Это трудная задача, которая до сих пор в общем случае не решена. (Точный смысл слов «существенно разных» — неизоморфных, см. ниже раздел 1.6.).