Методы расчета количества запасных частей, основанные на асимптотических формулах процессов восстановления

В табл. 13.21 приведены соответствующие формулы для простого и общего процессов восстановления. Считается, что асимптотические формулы дают точные оценки параметров Q.(L), oj (L), D (L) при наработке, превышающей величину переходного периода Ln.

Таблица 1321

Асимптотические зависимости для простого и общего процессов восстановления

Наименование.	Процесс восстановления.
	Простой.	Общий.
Ведущая функция потока отказов*.
Параметр потока отказов.

Наименование.	Процесс восстановления.
	Простой.	Общий.
Дисперсия числа отказов.
Переходный период**.

* L, Од — среднее значение и среднее квадратичное отклонение наработки до первого отказа; L, а — то же между отказами.

**Под переходным периодом здесь понимается пробег L_w при достижении которого дисперсия случайной величины числа отказов D (L) ~ 1.

С помощью асимптотических зависимостей производится интервальная оценка числа отказов Q (AL) на пробсте ДL = L_k~ L_H. Так, для верхней доверительной границы <2^И (ДL) имеем.

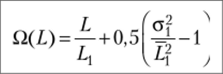
где u_p — квантиль нормального распределения, соответствующий доверительной вероятности Р.

На рис. 13.15 приведены асимптотические зависимости Q (L) для деления наработок, подчиняющихся нормальному и экспоненциальному законам (по данным табл. 13.20). Поскольку асимптотические формулы справедливы для любых законов распределения наработок между отказами, то различия между Q (L) определяются величиной коэффициента вариации v, а также соотношением между Ц и L(общий процесс восстановления). Например, прямые 1 и 2 (см. рис. 13.15) для простого процесса восстановления охватывают значения v от 0,3 до 1. Но в этом интервале находятся коэффициенты вариации для ряда законов распределения: Вейбулла, логарифмически нормального, гамма и т. д. Следовательно, асимптотические зависимости Q.(L) для нормального и экспоненциального законов позволяют оценить граничные значения для других законов распределения с коэффициентами вариации v, находящихся в интервале v_H 1.

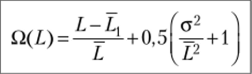
Рис. 13.15. Асимптотические зависимости для ведущих функций потоков отказов:

• 1 — простой процесс восстановления, экспоненциальный закон;
• 2 — то же, нормальный закон; 3 — общий процесс восстановления, экспоненциальный закон; 4 — то же, нормальный закон
• ? Разбор ситуации

Рассмотрим пример расчета количества деталей для парка транспортных средств с различным сроком эксплуатации, основываясь на асимптотических зависимостях, приведенных в табл. 13.21 для общего процесса восстановления.

В качестве рассматриваемого_узла возьмем карданный шарнир со средним пробегом до первого отказа L_{ = 120 тыс. км и отклонением а, = 50 гыс. км. Примем количество транспортных средств в соответствии с количеством лет эксплуатации Г, = 3, Г₂ = 4, Т₃ = 5, равное = 10, N₂= 25, N₃= 15.

Тогда период между отказами L и отклонение ст будут равны.

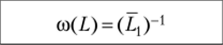
при принятых коэффициентах корреляционных зависимостей а₀, равными 22; 0,24 и 17; 0,2 соответственно.

Значение годовых пробегов для пяти лет службы автомобиля равны (тыс. км):

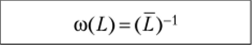
Результаты расчетов представлены также на графике (рис. 13.16).

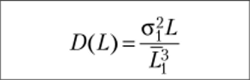
Рис. 13.16. Значение годовых пробегов для пяти лет службы автомобиля.

Проверим условие переходного периода: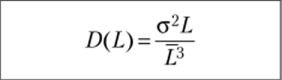

Определим значение ведущей функции отказов начального и конечного периода для группы Л', = 10 ед., Г, = 3 г.:

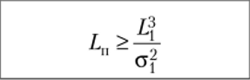
Тогда необходимое количество указанной детали для рассматриваемой группы и периода:

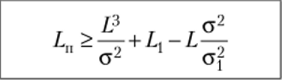
Аналогично рассчитываются параметры для оставшихся групп N₂ = 25, Л^гз= 15 с периодами Т₂=4, Г₃=5. Результаты расчетов приведены в табл. 13.22.

Таблица 13.22

Результаты расчетов с учетом различных сроков эксплуатации

Таким образом, как видно из табл. 13.22, суммарное прогнозное значение деталей с учетом срока эксплуатации групп транспортных средств — 66 шт. ?