Интерполирование. 
Химическая технология: научные основы процессов ректификации. 
Часть 2

Пусть функция у = /(х) при значениях аргумента Х|, х₂,…, х" принимает значения У, у_г,…, у_п, которые сведены в некоторую таблицу. И пусть необходимо определить значение у = /(х), (х_м < х < х₍). Значение х = х попадает между двумя табличными значениями, поэтому для вычисления значения функции необходимо предположить некоторый характер ее изменения между узловыми точками. Если закон изменения функции между узловыми точками предположить линейным, то для нахождения искомого значения можно воспользоваться уравнением прямой, проходящей через две точки,.

Такая замена функции /(х) на отрезке [х_м, х₍] прямой линией называется линейной интерполяцией, а точки х_м, х, — узлами интерполяции.

Если для данных значений функции линейная зависимость дает значительную погрешность, то можно воспользоваться квадратичной (параболической) интерполяцией у = ах² + Ьх + с, (а, Ь, с — коэффициенты, определяемые по трем прилежащим узловым точкам).

В общем случае зависимость, которой подчиняется функция, заданная таблично, может быть аппроксимирована многочленом и более высокой степени:

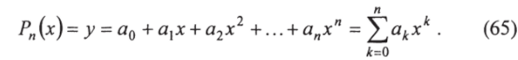
Тогда для определения коэффициентов этого многочлена необходимо располагать (п + 1)-й узловой точкой.

Геометрически задача построения многочлена Р" (х) степени п при интерполировании заключается в проведении кривой, проходящей через заданные точки. Уравнения вида (65) линейны относительно коэффициентов, поэтому аналитически определение коэффициентов интерполяционного многочлена для (и + 1) точек сводится к решению системы линейных уравнений (п + 1)-го порядка, каждое из которых представляет собой выражение (65), записанное для определенной узловой точки.

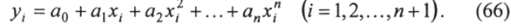
Система линейных уравнений (66) имеет единственное решение, если ее определитель.

Интерполяционный метод Лагранжа. Метод Лагранжа заключается в следующем.

Пусть в (п + 1)-й точке *о, ???, х" определены значения.

уо, Уи? ? •, у" — Требуется построить многочлен Р_п (х) степени не выше п, принимающий в узловых точках заданные значения.

Рассмотрим многочлен.

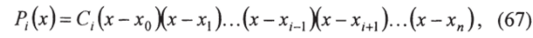
который в заданных точках удовлетворяет условиям.

Полагая x = x_t, из условий (68) можно найти значение константы С*:

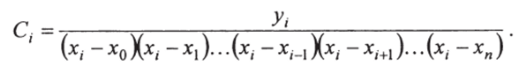
Теперь, подставляя полученное выражение в соотношение (67) будем иметь:

Таким образом, найден многочлен, принимающий в /-й точке заданное значение у, и равный нулю во всех остальных точках. Для того чтобы построить многочлен, принимающий значения уо, у> …" у_п в соответствующих точках, можно взять сумму.

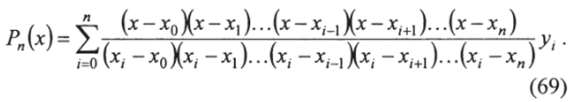
Этот многочлен называется интерполяционной формулой Лагранжа. Следует заметить, что при заданной совокупности узловых точек построение многочлена Лагранжа возможно только единственным образом. Действительно, если бы существовал другой многочлен степени п, то он как и первый, должен обращаться в нуль во всех узловых точках. Отсюда следует, что их разность была бы тождественно равна нулю, т. е. они должны совпадать.

Многочлен Лагранжа может быть построен при любом расположении узлов интерполяции. Однако, если для повышения точности интерполирования необходимо включить дополнительные точки, то все коэффициенты многочлена необходимо определять заново.

Пример 1. Построить интерполяционный многочлен Лагранжа, если заданы значения функции у = /(*):

Решение. Здесь п = 3. Применяя формулу (69), получим:

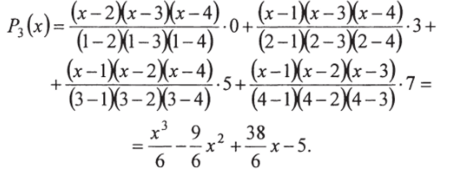
Конечные разности. Пусть некоторая функция у = f (x) в точках хо, хо + h, хо + 2h и т. д. принимает значения уо, у,? ??, у_п, где h — шаг интерполяции.

Выражения.

называются первыми конечными разностями функции у = f (x). Символ Д называется разностным оператором и означает, что функции у = f (x) ставится в соответствие функция Ду = f (x + h)~ f{x). Поскольку разностный оператор может применяться многократно, можно получить разности второго, третьего и более высоких порядков. Все разности порядка выше первого определяются через разности на единицу меньшего порядка, однако могут выражаться и через разности и более низкого порядка или через значения функции. Например, для заданной функции /(х) разности второго порядка есть:

Аналогично строятся конечные разности более высокого порядка:

Конечные разности первого, второго и т. д. порядков удобно представлять в виде таблиц разностей. Для функции у — /(х) конечные разности приведены в табл. 3.

Таблицы разностей используются при обработке экспериментальных данных и, в частности, при интерполировании и экстраполировании функций.

Интерполяционные формулы Ньютона. Пусть для функции у = /(х) заданы значения y_t — /(х,) при равноотстоящих значениях аргумента x_i=x₀+ih (г = 0,1,2,…, и). Требуется построить многочлен Р"{х) степени не выше п, принимающий в точках х, значения.

При интерполировании по Ньютону многочлен Р_п(х), удовлетворяющий этому условию, может определяться двумя способами:

Если интерполяционный многочлен строится в виде уравнения (70), то получается формула Ньютона для интерполирования вперед, если же в виде (71), то формула Ньютона для интерполирования назад. Выбор формулы определяется той частью табличных значений, которая будет интерполироваться впоследствии. Формула (70) более удобна для интерполирования начальных значений функций, а формула (71) — наоборот, конечных.

Формулы Ньютона позволяют легко изменять число узлов интерполирования, а следовательно, и степень многочлена. Действительно, при увеличении числа точек на единицу соответственно на единицу увеличится число членов многочлена и его степень, причем наивысшая степень будет соответствовать последнему члену многочлена.

Определение коэффициентов формул (70) и (71) производится аналогично, поэтому ниже будет рассмотрен только порядок получения коэффициентов формулы (70).

Задача построения многочлена вида (70) заключается в определении коэффициентов а₀, а₁, а₂,…, а_п и может быть решена следующим образом. Полагая х = xq и подставляя это значение в (70), получим Отсюда, а₀= у₀.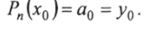

Для определения коэффициента а в уравнение (70) необходимо подставить значение х = х,.

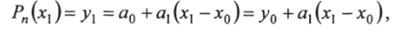
откуда.

где л’уо = А¹ У (дг) = /(х₀ + Дх)-/(лг₀) — первая конечная разность.

Для определения коэффициента аг подставим в уравнение (70) х = х₂: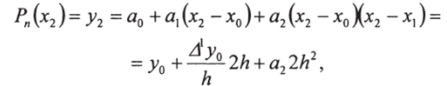

откуда.

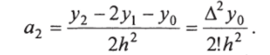
Продолжая подстановку значений x_i (г = 3,4,…), можно получить соответственно

Подставляя найденные значения коэффициентов а₀, а,…, а_п в уравнение (70), получим.

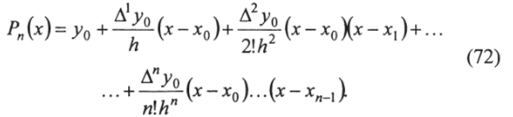
Этот многочлен называется формулой Ньютона для интерполирования вперед.

Формулу Ньютона для интерполирования назад можно получить, если последовательно в уравнение (71) подставить значения х_п, х_п_₁,…, х₁

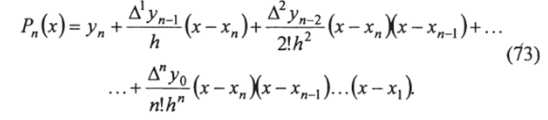
Таким образом, для построения многочлена Ньютона степени п необходимо вычислить конечные разности до я-го порядка. При этом добавление узлов интерполирования не приводит к пересчету ранее вычисленных коэффициентов.

Пример 2. Построить интерполяционный многочлен Ньютона для заданных значений функции у — f (x)

Решение. Здесь п = 3, h = 1.

Составим таблицу конечных разностей функции у = /(*) (табл. 4).

Воспользовавшись формулой (72) получим.

Тот же результат может быть получен, если воспользоваться формулой (73) для интерполирования назад:

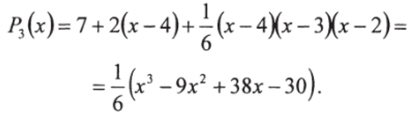
Заметим, что многочлен Лагранжа, построенный по этим же точкам, совпадает с многочленами Ньютона. Следовательно, если дана (я + 1)-а узловая точка, то независимо от способа построения многочлена степени не выше я, проходящего через заданные точки, последний определен однозначно в пределах ошибок округления.

Пример 3. Пусть задана относительная плотность раствора карбоната натрия при 30 °C (по отношению к плотности воды при 4°С):

Состав, % 4 8 12 16 20 24 28.

Плотность, 1,0363 1,0775 1,12 1,1636 1,2086 1,2552 1,3031.

г/см

Таблица 5. Конечные разности для примера 3

Определить плотность 30%-го раствора карбоната натрия. По этим данным построим таблицу конечных разностей (табл. 5).

Из табл. 5 следует, что:

• — для экстраполяции можно воспользоваться полиномом третьей степени, тогда точность не будет превосходить единицы четвертого разряда;
• — последнее значение разности Aⁱd получено из х = 16, поэтому это значение аргумента следует выбрать в качестве хо для формулы (72).

Применяя интерполирование вперед, запишем d_i0 = = f (x)= f (x₀ + kh). Поскольку хо = 16; h = 4; х = 30, то.

к _ 30−16 _з 5 4.

Тогда, используя формулу (72), можно записать:

(по справочнику t/зо = 1,3274).

Оценка точности формул интерполирования. Интерполяционный многочлен независимо от способа его получения аппроксимирует исходную функцию с некоторым приближением. Поэтому естественно поставить вопрос о степени его приближения к функции в точках, отличных от узловых, т. е. оценить остаточный член интерполяции.

Оценка остаточного члена интерполяции обычно производится аналогично оценке остаточного члена при разложении функции в ряд Тейлора. При использовании этого способа необходимо, чтобы функция j{x) имела все производные до (п + 1)-го порядка включительно. Поскольку выражение (74) обращается в нуль в (п + 1) точках, можно записать, что.

Теперь выберем К (х) так, чтобы для произвольного х е [хо, х"] вспомогательная функция Щх) обращалась в нуль:

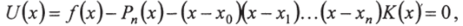
откуда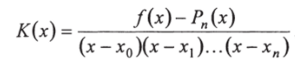

Очевидно, при таком выборе К (х) функция U (х) будет иметь по крайней мере (и + 2) корня на интервале определения /(х), включая концевые точки, и по теореме о среднем ее производная обращается в нуль, по крайней мере в (и + 1)-й точке. Выполняя дифференцирование функции U (х) (и + 1) раз для произвольного х отрезка определения функции /(х), получим:

Поскольку U (д:) имеет (п + 2) корня, то ее (п + 1)-я производная в некоторой точке х е [x₀, х_п ] также обращается в нуль, т. е. ?Л^я+|)(х) = 0.

Следовательно,

и для остаточного члена интерполяции можно записать:

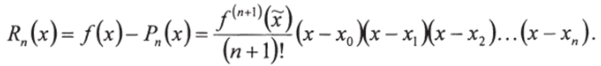
Для оценки возможной максимальной ошибки интерполирования вместо /*^я+|*(3с) используется величина.

Тогда максимальная ошибка интерполяции не превосходит величины.

Как следует из выражения (75), ошибка определяется максимальной величиной производной /*^л+|*(;с). Если высшие производные функции малы, то мала и ошибка приближения. Однако для некоторых функций их высшие производные ведут себя как п. Поэтому не всегда повышение степени интерполяционного многочлена может привести к уменьшению ошибки аппроксимации. Может даже оказаться, что меньшая степень обеспечивает более высокую точность представления функции.

Ошибка, обусловленная большой величиной высших производных, не может быть изменена, она определяется характером функциональной зависимости. Для функций, заданных таблично и не имеющих аналитического представления, ее подчас невозможно оценить. Однако как следует из выражения (75) ошибка, вызванная неудачным выбором узловых точек, также может быть существенной. Если, например, узлы интерполяции будут выбраны вблизи одного из концов интервала интерполирования, то для значений х, у второго конца интервала при (х_п — х₀) > 1 разности будут значительными, соответственно их произведение может быть сравнимо со значением производной. Поэтому при интерполировании с неравноотстоящими узлами выбор узловых точек необходимо производить таким образом, чтобы значение полинома в правой части соотношения (75) для различных значений аргумента было возможно малым по абсолютной величине.