Корреляционное отношение. 
Общее представление о внутригрупповом и межгрупповом разбросе

Сущность новой меры связи — корреляционного отношения — продемонстрируем на примере, заимствованном из уже упоминавшейся работы Гласса и Стэнли (с. 138—139).

Изучается зависимость результатов ответа респондента на вопросы некоторого теста (Y) от его возраста (X). Опрашивалось 28 человек. По возрасту они были разделены на 8 групп, каждая группа характеризуется средним возрастом попавших в нее респондентов (например, возраст 30 приписан всем людям, попавшим в возрастной интервал от 28 до 32 лет). Статистические данные представлены на рис. 13.3 и табл. 13.2.

На рис. 13.3 видно, что наблюдаемые точки довольно плотно расположены вокруг ломаной линии. Это наводит на мысль о том, что указанная ломаная линия отражает определенную тенденцию: с изменением возраста от 10 до 22 лет показатели людей порассматриваемому тесту растут, затем начинается спад. И говорить об этой тенденции мы можем только благодаря тому, что, во-первых, если для каждого рассматриваемого значения возраста вычислить среднее арифметическое значение зависимой переменной, ломаная линия пройдет через соответствующую точку; во-вторых, для каждой возрастной группы разброс значений теста вокруг упомянутой средней относительно небольшой. Это интуитивное соображение можно формализовать. Соответствующая формализация и лежит в основе рассматриваемого коэффициента связи.

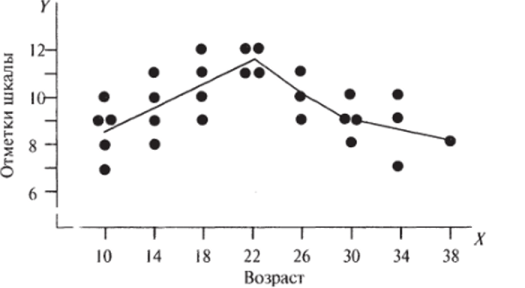
Рис. 13.3. Пример данных для расчета корреляционного отношения: связь между возрастом и характеристикой 28 человек по вспомогательному тесту цифра-знак шкалы интеллекта взрослых Векслера (WAIS).

Введем несколько новых понятий. Обозначим через Y среднее арифметическое значение зависимой переменной для j-й группы (j — 1,…, J). Отметим, что точка перед индексом j в обозначении среднего арифметического означает, что по первому индексу величины Y. произошло суммирование.

Определение. Внутригрупповая сумма квадратов

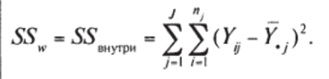
Таблица 13.2. Ответы респондентов на заданный тест в зависимости от их возраста (данные для расчета корреляционного отношения).

Y. — значение зависимого признака для /-го респондента ву-й возрастной группе; i = I,…, я, где п. — число членову-й группы;у = I,… /, где J — количество выделенных групп (в данном случае J = 8).

В нашем примере эта сумма будет равна:

• (7−8,60)² + (8−8,60)² + (9−8,60)² + (9−8,60)² + (10−8,60)² + …
• (для первой группы)
• (8−9,50)² + (9−9,50)² + (10 — 9,50)² + (11−9,50)² + …
• (для второй группы)

+ (8−8,00)²= 24, 87 (для восьмой группы).

Обозначим через К. среднее арифметическое всех значений независимого признака. Очевидно, что имеет место соотношение:

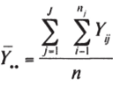
j.

где п = 2) = я, + +… + tij — объем выборки.

н

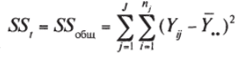
Определение. Общая сумма квадратов —.

Определение. Корреляционное отношение — разность В ^{1 _} (ss^/ss^j.

Для рассмотренного примера, что нетрудно проверить, имеют место соотношения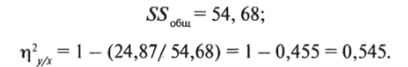

Поясним смысл корреляционного отношения. Суть любого коэффициента легче понять, если рассмотреть, при каких условиях он принимает максимальное (в данном случае — 1) и минимальное (0) значение. Ясно, что т² . = 1, когда SS _т = 0, т. е. когда в каждой вы;

у/х внутри деленной по признаку Xгруппе (в нашем случае — в каждой возрастной группе) значения признака Кодинаковы. В нашем примере это означает, что все точки лежат на выделенной ломаной линии, что действительно говорит о наличии криволинейной связи.

Что касается равенства у² = 0, оно имеет место в том случае, когда S'5_внутри = 55_о6ш, т. е. когда фиксация признака X нисколько не уменьшает разброс признака У. Это говорит об отсутствии связи: получение информации об^не увеливает информацию об У. Здесь напрашивается аналогия с принципом построения коэффициентов связи, основанных на прогнозных моделях⁸¹.

Коэффициент г²_у/х — мера степени предсказания УпоХс помощью «наилучшим образом подобранной» линии, либо прямой, либо кривой.

Заметим, что г²_у/х * г²_ф (о подобной перестановке признаков можно говорить только в случае, если оба признака измерены по интервальной шкале; хотя для измерения одного из означенных коэффициентов, скажем, Ц²_у/Х, достаточно того, чтобы У был интервальным, Л' может быть и номинальным).

Поясним на примере: если человеку 10 лет, можно довольно уверенно предсказать, что результатом тестирования для него будет балл, равный 8,60. Однако если некий человек получил балл 8,60, то его возраст может быть с одинаковой вероятностью как малым (10 лет), так и большим (38 лет). Значит, можно довольно точно предсказать У по /V, но нельзя хорошо прогнозировать X по К Это неизбежно отражается на величинах х]²_у/х и у]²^: г]²_у/х =0,545, а ц²_к/у близка к нулю. Нс будем ее вычислять, так как вычисление потребовало бы перегруппировки данных. Ячейки должны были бы быть организованы по результатам тестирования (скажем, можно было бы сформировать три ячейки — в первую включить респондентов, получивших баллы 7—8, во вторую — баллы 9—10, в третью — баллы 11 — 12). А в каче;

^к| Толстова Ю.Н. Анализ социологических данных.

стве значений У выступал бы возраст респондентов, вошедших в ту или иную ячейку.

Приведем еще один пример.

Пример. Дана частотная таблица.

Рассчитать корреляционное отношение г²_у/х.

Решение. Вспомним, что, разбив диапазон изменения признака на интервалы и составив частотную таблицу, мы потеряли исходную информацию и вынуждены считать, что респонденты, попавшие в один интервал, имеют одну и ту же зарплату, отвечающую середине этого интервала.

Расположим данные в более привычном (часто использующемся при нахождении корреляционного отношения) виде. Правда, не будем выписывать конкретные зарплаты (У) для людей, попавших в ту или иную возрастную группу (возраст — А), а укажем, сколько человек обладают тем или иным значением.

Общее среднее по Y :У" — 600 (10 + 10 + 5) + 800 (5 + 10 + 20) + + 1000 (5+ 20+ 20)/100 = 880;

55_об1ц = (600 — 880)² (10 +10 + 5) + (800 — 880)² (5+10+20) + (1000 — - 880)² (5+ 20 + 20) = 2 832 000;

К, = (600×10 + 800×5 + 1000×5) / 20 = 750;

К ₂ = (600×10 + 800×10 + 1000×20) / 40 = 850;

У з = (600×5 + 800×20 + 1000×20) /45 = 866,7;

^внутри = (⁶⁰⁰ — К, У х 10 + (800 — К,)²X 5 + (1000 — К,)² х 5 + (600 — - К₂)² х 10 + (800 — У,₂)² х 10 + (1000 — У₂)² х 20 +(600 — Г ₃)² х 5 + + (800 — К ₃)²х 20 + (1000 — К ₃)²х 20 = 150²х 10 + 50²х 5 + 250² х 5 + + 250² х 10+ 50² х 10 + 150² х 20 + 267² х 5 +67² х 20 + 133² х 20 = =2 449 945;