Уравнения состояния для практического применения

Для решения многих научных и инженерных задач необходима информация о свойствах веществ, в частности о термодинамических свойствах. Для большинства веществ, используемых в технике, подобная информация представлена в виде таблиц и графиков, а также в виде коэффициентов аппроксимирующих функций. Сведения такого рода хранятся в справочниках и машиночитаемых базах данных.

Для расчета свойств чистых веществ и их смесей широко используются уравнения состояния. Наиболее эффективные и универсальные уравнения состояния используются при разработке компьютерных программ для моделирования термодинамических процессов. В большинстве случаев пользоваться такими программами удобнее, чем графиками и таблицами, однако всегда необходимо помнить о возможных пределах их применимости и о точности результатов моделирования при анализе реальных процессов.

В настоящее время известно довольно много уравнений состояния реального газа. Большинство из них имеет ограничения как по списку веществ, так и по диапазону применимости. Относительно универсальные уравнения состояния можно разделить на три группы:

• 1) расширенное вириальное уравнение состояния;
• 2) кубические уравнения состояния, в основу которых положен расширенный принцип соответственных состояний;
• 3) уравнения состояния, полученные с использованием методов молекулярной физики.

В 1901 г. голландский физик X. Камерлинг-Оннес предложил вириальное уравнение состояния в форме полиномиального разложения по степеням v и Т

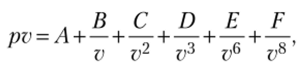
где A = RT; B = b{T + b₂ ⁺у^_+^'⁺-*; С-с{Г+с₂+у-+^-+…;…

Точность описания p—v—Tданных можно увеличивать за счет увеличения числа коэффициентов.

Более современная форма вириального уравнения состояния основана на использовании модельного потенциала межмолекулярного взаимодействия и выглядит следующим образом:

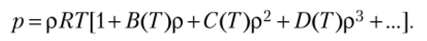
Вириальные коэффициенты В, С, D, … вычисляются с использованием параметров модельного потенциала межмолекулярного взаимодействия и (г), например, с использованием параметров потенциала Леннард-Джонса.

В частности, второй вириальный коэффициент можно рассчитать по формуле.

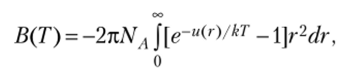
где N_a — число Авогадро; k — постоянная Больцмана.

Несколько первых коэффициентов вириального уравнения можно рассчитать с использованием параметров потенциала Леннард-Джонса, которые достаточно просто оценить, см. например [1]. В области, достаточно удаленной от критической точки, вириальное уравнение состояния с приемлемой для инженерных целей точностью позволяет описать свойства чистого газа и газовых смесей. Поэтому его целесообразно использовать для моделирования состояний и процессов с участием газовой фазы в области высоких температур и давлений.

При выборе уравнения состояния обычно приходится искать компромисс между простотой уравнения, доступностью его параметров и точностью описания данных экспериментов.

Уравнение Бенедикта — Вебба — Рубина —

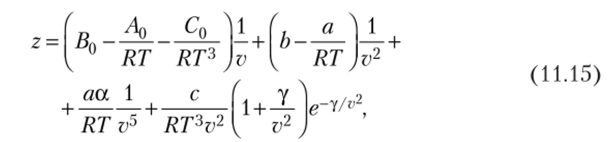
где Aq, В₀, С₀, а, Ь, с, а, у — параметры уравнения состояния. Соотношение (11.15) позволяет с высокой точностью описать экспериментальные данные о сжимаемости веществ в широком диапазоне температур и давлений. Главным его недостатком является большое число коэффициентов.

В химической технологии и при решении ряда теплофизических задач в области сосуществования пара и жидкости широко применяются кубические уравнения состояния. Одно из них, уравнение Ван-дер-Ваальса, мы уже рассмотрели. В 1949 г. было предложено более точное уравнение состояния Редлиха — Квота

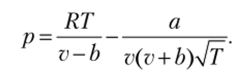
Это уравнение состояния напоминает уравнение Ван-дер-Ваальса.

Если давление выражено в барах, температура — в кельвинах, объем — в кубических сантиметрах на моль, а и b имеют размерности бар • (см³/моль)² и см³/моль соответственно. Тогда уравнение Редлиха — Квонга можно записать в виде.

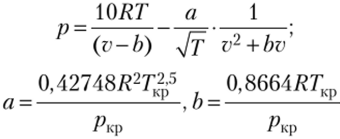
В различных модификациях уравнения Редлиха — Квонга используется дополнительный эмпирический параметр — фактор ацентричности ю, который характеризует степень отклонения межмолекулярного потенциала и (г) данного вещества от межмолекулярного потенциала и'(г) сферической молекулы вещества сравнения:

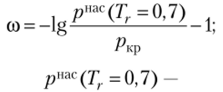
давление насыщенного пара при Т_г = Т/Т_Щ) =0,7.

Уравнение состояния Соава —.

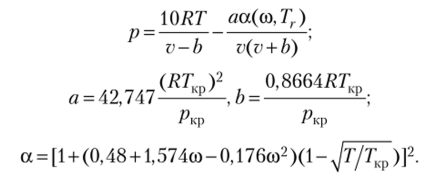
Зависимость а (со, Т_Г) получают путем обработки экспериментальных данных.

Уравнение состояния Пета — Робинсона —

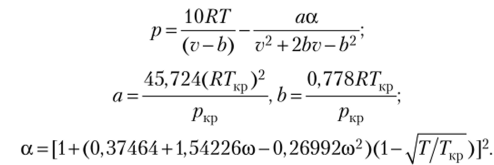
Уравнение состояния Редлиха — Квота — Пета — Робинсона (RK —.

PR) [2] -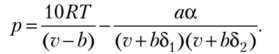

Для 0,171 < 2_кр < 0,29.

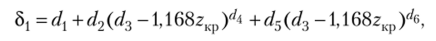
где 5₁ — безразмерная величина (б/р). Если z_Kp >0,29, то 8) =V2−1.

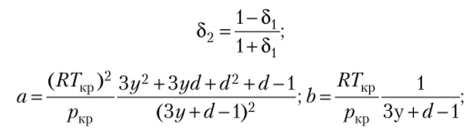
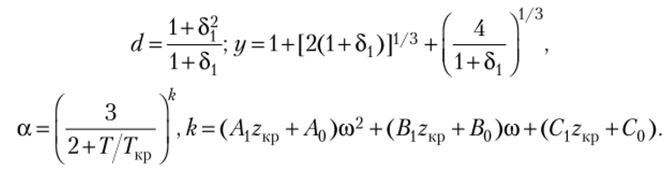
Значения коэффициентов приведены в табл. 11.2. Уравнение состояния Редлиха — Квонга — Пента — Робинсона является одним из наиболее точных кубических уравнений состояния на сегодняшний день.

Таблица 11.2

Коэффициенты уравнения RK — PR.

С помощью уравнений состояния кубического типа можно моделировать поведение как полярных, так и неполярных веществ. Важным достоинством кубических уравнений состояния является то, что с их помощью можно описывать свойства газовой и жидкой фаз в двухфазной области. При этом число коэффициентов уравнения состояния относительно невелико. Такие уравнения состояния успешно применяются для анализа фазовых равновесий и в многокомпонентных системах. Однако кубические уравнения состояния часто довольно плохо описывают линию насыщенной жидкости в координатах/?—?;, которая проходит практически вертикально вследствие малой сжимаемости жидкости. Это объясняется тем, что отталкивательный член в уравнении состояния моделируется неудовлетворительно.

Для того чтобы уравнение состояния могло описывать свойства газа и жидкости одновременно, необходимо, чтобы оно имело вид.

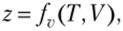
поскольку в этом случае наличие нескольких корней решения дает возможность выделить из них объем жидкой фазы и объем паровой фазы. При этом функция/_г(Г, У) должна быть, по крайней мере, кубической относительно объема.

Иногда можно встретить термин «аналитическое» уравнение состояния. Этот термин следует понимать двояко. С одной стороны, речь может идти о том, что уравнение состояния представлено в аналитической форме. В некоторых случаях уравнение состояния задается в табличном виде. С другой стороны, уравнение состояния называется аналитическим, если его корни могут быть вычислены аналитически, а не численно. Это означает, что функция f_v(T, V) не должна содержать степеней V выше четвертой.

Пример 11.1.

Параметры критической точки воды: Г_кр =647 К, р_кр = 220,6 бар,.

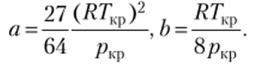
Рассчитайте постоянные, а и Ь в уравнении Ван-дер-Ваальса для воды. Решение

Выберем размерности коэффициентов:

Рассмотрим еще один пример.

Пример 11.2.

Давление в баке объемом 24 м³ не должно превышать 105 бар. Оцените величину давления в баке, если в нем находится 1000 кг водяного пара при температуре 360 °C. Использовать в расчетах три уравнения состояния: идеального газа, Ван-дерВаальса и Редлиха — Квонга.

Параметры уравнений состояния:

• (м³ У М³
• • Ван-дер-Ваальса — а-5,531 бар —; 6 = 0,0305-;

^ кмоль ) кмоль.

• (М³ f — м³
• • Редлиха — Квонга: — а = 142,59 бар — К⁰⁵; 6 = 0,0211-.

Решение кыот>) кмоль.

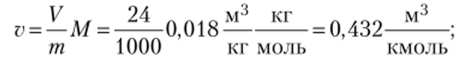
RT 8,314 10³ *633 ,_OIQ<

1) уравнение идеального газа — р = — =-= 121,8 бар;

v 0,432.

2) уравнение Ван-дер-Ваальса —