Теорема Остроградского — Гаусса

Пусть в пространстве задано векторное поле, которое представлено зависимостью.

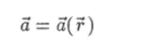
некоторого вектора, а от радиус-вектора г. Поток вектора, а через замкнутую поверхность S обозначается так:

где вектор п есть внешняя нормаль к поверхности.

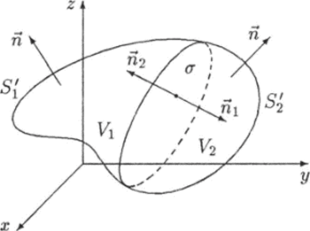
Рис. 12.11. К доказательству теоремы Остроградского — Гаусса.

Замкнутая поверхность S всегда ограничивает некоторый объем V. Разделим этот объем на две части V и Vi поверхностью а (рис. 12.11), которая делит поверхность S также на две части и S'₂: S = S[ + S‘₂- Поверхность S, ограничивающая объем V, состоит из поверхностей и a: S — + <�т, а поверхность ограничивающая объем 1^, — из 5^ и.

ст: Si = S’i + (т. Поэтому потоки вектора а через замкнутые поверхности Si и Si в направлении внешних нормалей к этим поверхностям можно записать так:

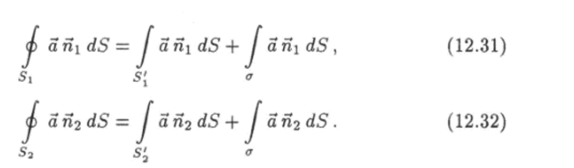
На границе раздела <�т внешние нормали ni и П2 к поверхностям S и соответственно таковы, что.

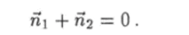
С учетом этого условия сложение равенств (12.31) и (12.32) дает.

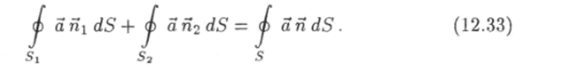
Таким образом, приходим к выводу, что сумма потоков через поверхности, ограничивающие объемы V и V2, равна потоку через поверхность, ограничивающую объем V + V2. В свою очередь каждый из объемов V и V2 можно также разделить на две части. Эту операцию можно проделать сколько угодно раз. Применяя при каждом разделении формулу (12.33), докажем в результате следующее утверждение. Сумма потоков некоторого вектора а через поверхности 5,-, ограничивающие объемы К" которые все вместе составляют объем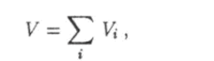

равна потоку этого вектора через поверхность 5, ограничивающую объем.

V:

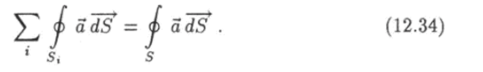
Вычислим поток вектора а через поверхность бесконечно малого параллелепипеда, ребра которого параллельны координатным осям х, у, z и равны соответственно dx, dy_} dz (рис. 12.12). Параллелепипед имеет шесть граней. Грань S параллельна плоскости x-z, проходит через точку (х, у, г), а ее площадь равна dxdz. Внешняя нормаль к этой грани п = — j. Поэтому поток вектора а через поверхность Si будет.

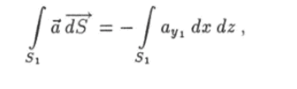
где a_yi = (i_y(P) — проекция вектора а на ось у как функция точки Р € S1. Так как размеры грани S бесконечно малы, функцию а_У1 можно заменить ее значением в любой точке этой грани. Положим а_Ух = а_у(х, у, z). Получим^-

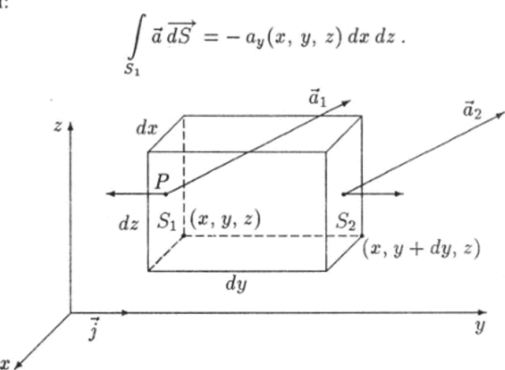
Рис. 12.12. К доказательству теоремы Остроградского — Гаусса.

Таким же образом найдем поток вектора а через грань 5 г, которая также параллельна плоскости x-z, но проходит через точку (х, y + z):

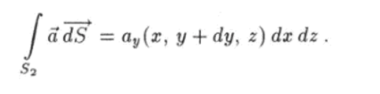
Согласно определению частного дифференциала функции нескольких переменных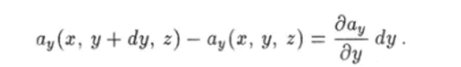

С учетом этого равенства сумма потоков вектора а через грани S и 5 г будет равна.

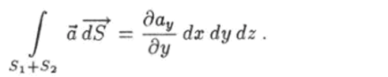
Повторяя эти действия при вычислении потоков вектора а через другие пары граней, найдем в результате их сложения полный поток этого вектора через поверхность S параллелепипеда:

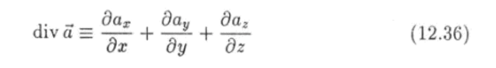
называется дивергенцией вектора а. В силу свойства (12.33) равенство (12.35) справедливо для бесконечно малого объема любой формы.

Разделим произвольный объем V на множество бесконечно малых объемов dV_} для каждого из которых справедливо равенство (12.35). Суммируя левые и правые части этих равенств, с учетом свойства (12.34) получим:

где S — поверхность, ограничивающая объем V. Равенство (12.37) составляет содержание теоремы Остроградского — Гаусса (Михаил Васильевич Остроградский (1801 — 1861) — русский математик, Карл Гаусс (1777 — 1855) — немецкий ученый). Согласно этой теореме поток вектора, а через произвольную воображаемую замкнутую поверхность S ь направлении внешней нормали равен объемному интегралу от дивергенции этого вектора по объему V, заключенному внутри поверхности S.