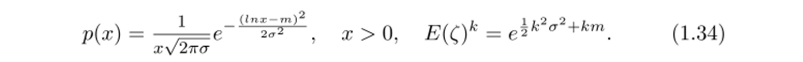Численное решение СДУ с растущей дисперсией

Во второй главе учебного пособия [31] предложен способ сведения исходной неустойчивой системы СДУ к системе СДУ с решением, близким к стационарному процессу [39]. С использованием формулы дифференцирования Ито получены системы СДУ для стохастической составляющей как в случае линейной, так и нелинейной исходной системы СДУ. Для трех конкретных задач, имеющих решение с растущей дисперсией, выписаны соответствующие им в новых переменных стационарные в широком смысле СДУ. Также излагаются классические методы уменьшения дисперсии оценок функционалов применительно к численному решению СДУ.

Продемонстрируем данную методику при решении конкретной задачи.

Уравнение (формула (2.33) учебного пособия [31]) решалось на интервале [0,10] при а = 0, s = 1 но точной формуле (см. формулу (2.34) учебного пособия [31]) с шагом h = 10 и оценивалось математическое ожидание т_у(10). В качестве начального значения задавалось уо = е^, где? € N (0,1). Напомним, что если? нормальная случайная величина со средним га и дисперсией а², то? = ^ ~ логарифмически нормальная случайная величина с плотностью р (х) и моментами А>порядка:

Поэтому первый и второй момент точного решения при t = 10 равны: Еу ( 10) = 1.649, Еу²(10) = 162 754.8.

С помощью замены (формула (2.38) учебного пособия [31]) был осуществлен переход от уравнения (формула (2.33) учебного пособия [31]) к уравнению (формула (2.41) учебного пособия [31]), которое на интервале [0,10] при а = 0, s = 1 решалось методом Эйлера с шагом h = 0.01. В момент времени t = 10 вычислялось статистическое среднее переменной га_х(10), а затем (форм}'ла (2.40) учебного пособия [31]) вычислялась оценка математического ожидания переменной га_у(10). В табл. 1.5 для различных объемов выборки N в момент Т = 10 приводятся полученные оценки математического ожидания обоими методами.

Численное исследование предложенного способа решения СДУ с растущей дисперсией, проведенное на одномерном уравнении, показало, что данный метод действительно позволяет более точно оценивать функционалы от решения, в частности, математическое ожидание. Также.

интересно исследование предложенного способа при проведении комплексных численных экспериментов для трех типов задач, в которых возникает явление неустойчивости: 1) линейный осциллятор, 2) уравнение Ван дер Поля, 3) краевые задачи математической физики.