Условные законы распределения. 
Числовые характеристики двумерной случайной величины. 
Регрессия

Определение. Условным законом распределения одной из одномерных составляющих двумерной случайной величины (X, У) называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение {или попала в какой-то интервал)

Выше (параграф 5.1) рассмотрено нахождение условных распределений для дискретных случайных величин. Там же приведены формулы (5.1) и (5.2) условных вероятностей:

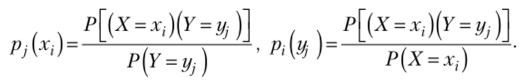
В случае непрерывных случайных величин необходимо определить плотности вероятности условных распределений ср_(/ (х) и ф_х[у). С этой целью в приведенных формулах заменим вероятности событий их «элементами вероятности», т. е. Р[(Х = Х;)(У-у,)] на <�р (д, у) дхду, Р{Х = х,) на ф (х)г/х, Р (У = у_}) на <�р (г/) ду, Р/х,) на (р,_у {х)(1х и Р,{у_}) на ф, {у) (?у, после сокращения на (1х и (1у получим:

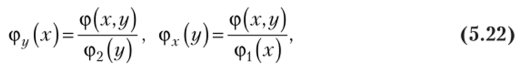
т.е. условная плотность вероятности^[1] одной из одномерных составляющих двумерной случайной величины равна отношению ее совместной плотности к плотности вероятности другой составляющей.

Соотношения (5.22), записанные в виде.

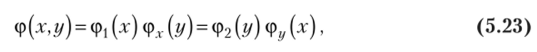
называются теоремой (правилом) умножения плотностей распределений.

Используя формулы (5.20), условные плотности вероятностей (5.22) можно выразить через совместную плотность следующим образом:

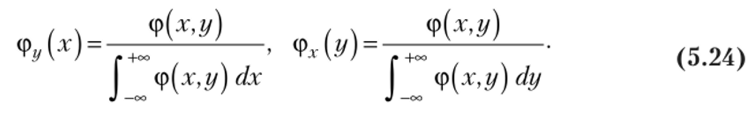aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">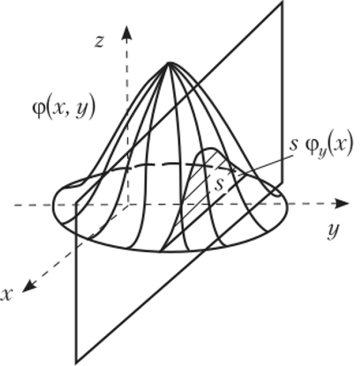

Рис. 5.9.

Если, как отмечено выше, совместная плотность ф (х, у) двумерной случайной величины представляет собой геометрически некоторую поверхность распределения, то, например, условная плотность ф_/у(х) есть кривая распределения, подобная сечению этой поверхности плоскостью У = у, параллельной координатной плоскости Охг и отсекающей на оси Оу отрезок у (рис. 5.9), и в соответствии с (5.24) и замечанием на с. 172 получается из нее делением всех ординат на площадь данного сечения 5 (т.е. сечение поверхности распределения есть кривая 5 фДх), где 0 < 5 < 1) (см. рис. 5.9).

Аналогично можно пояснить геометрически и смысл условной плотности ф_д.(г/).

Условные плотности ц>_у(х) и ф_х{у) обладают всеми свойствами «безусловной» плотности, рассмотренной в гл. 3.

Числовые характеристики одномерных составляющих X и У и их условных распределений — математические ожидания М (Х), М (У) и дисперсии О (Х), 0(У), условные математические ожидания М_у{Х) и М_Х(У) и условные дисперсии ДДХ) и О_х(У) находятся по обычным формулам математического ожидания и дисперсии, в которых используются соответствующие вероятности или плотности вероятностей (табл. 5.3).

Условное математическое ожидание случайной величины У при условии X = х, т. е. М_х(У)_у есть функция отх_} называемая функцией регрессии или просто регрессией У по X; аналогично М,_у(Х) называется функцией регрессии или просто регрессией X по У. Графики этих функций называются соответственно линиями регрессии (или кривыми регрессии) У по X и X по У^[2]. Функции (линии) регрессии характеризуют изменение в среднем одной случайной величины при изменении другой.

Основные свойства условных математических ожиданий и дисперсий аналогичны свойствам их «безусловных» аналогов, отмеченных выше (см. параграфы 3.3, 3.4); при этом надо учитывать, что проводимые в них операции понимаются теперь уже не как действия над числами, а как действия над функциями.

Таблица 5.3.

Характеристики	Дискретные случайные величины	Непрерывные случайные величины

Примечание. Условные вероятности я. Д. т,), р,.(у,) и условные плотности (р_;/(х), <�р_х(у) находятся соответственно по формулам (5.1), (5.2). (5.22).

Отметим здесь некоторые дополнительные свойства условного математического ожидания.

1. Если Z = g (X), где g — некоторая неслучайная функция от X, то 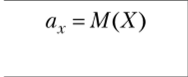В частности,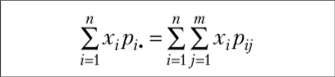

{правило повторного ожидания).

• 2. Если г = g (X)_y то М_Д(7У) = 7 М_Д (У).
• 3. Если случайные величины X и Унезависимы, то

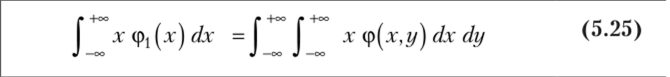
? Докажем в качестве примера (для непрерывной случайной величины) правило повторного ожидания М (М_Х(У)) = М (У). Условное математическое ожидание М_Х(У) находится по условному распределению случайной величины У (при условии, что X = х), задаваемому условной плотностью вероятности ср_д.(У). По формуле (5.27') с учетом равенства (5.22) получим Теперь

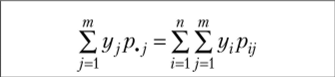
(в соответствии с формулой (5.25')). ?

• [1] 2 Для условных плотностей вероятности используются также обозначения <�р (л' | у), (р (г/1 х).
• [2] Говорят также: У на X и X на У.