Оценка вероятности (биномиального распределения) по относительной частоте

Пусть производятся независимые испытания с неизвестной вероятностью р появления события Л в каждом испытании. Требуется оценить неизвестную вероятность р по относительной частоте, т. е. надо найти ее точечную и интервальную оценки.

А. Точечная оценка. В качестве точечной оценки неизвестной вероятности р принимают относительную частоту.

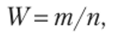
где т — число появления события Л п — число испытаний^[1].

Эта оценка несмещенная, т. е. ее математическое ожидание равно оцениваемой вероятности. Действительно, учитывая, что М (т) = пр (см. гл. 7, § 5), получим.

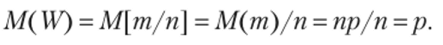
Найдем дисперсию оценки, приняв во внимание, что D (m) = npq (см. гл. 7, § 6):

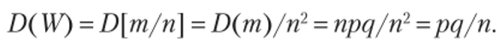
Отсюда среднее квадратическое отклонение.

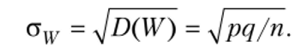
Б. Интервальная оценка. Найдем доверительный интервал для оценки вероятности по относительной частоте. Напомним, что ранее (см. гл. 12, § 6) была выведена формула, позволяющая найти вероятность того, что абсолютная величина отклонения не превысит положительного числа 8:

где X — нормальная случайная величина с математическим ожиданием М (Х) = а.

Если п достаточно велико и вероятностьр не очень близка к нулю и к единице, то можно считать, что относительная частота распределена приближенно нормально, причем, как показано в п. А, М (W)-р.

Таким образом, заменив в соотношении (*) случайную величину X и ее математическое ожидание а соответственно случайной величиной W и ее математическим ожиданием р, получим приближенное (так как относительная частота распределена приближенно нормально) равенство.

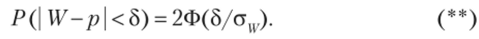
Приступим к построению доверительного интервала (p_vp₂)* который с надежностью у покрывает оцениваемый параметр р> для чего используем рассуждения, с помощью которых был построен доверительный интервал в гл. 16, § 15. Потребуем, чтобы с надежностью у выполнялось соотношение (**):

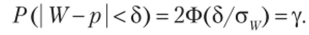
Заменив c_w через yjpq/n (см. п. А), получим.

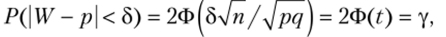
где t = b4n/yfpq.

Отсюда.

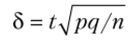
и, следовательно,.

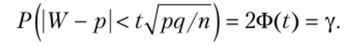
Таким образом, с надежностью у выполняется неравенство (чтобы получить рабочую формулу, случайную величину Wзаменим неслучайной наблюдаемой относительной частотой w и подставим 1 -р вместо q):

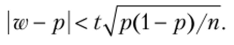
Учитывая, что вероятностьр неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда

Обе части неравенства положительны; возведя их в квадрат, получим равносильное квадратное неравенство относительно/?:

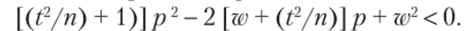
Дискриминант трехчлена положительный, поэтому его корни действительные и различные:

меньший корень.

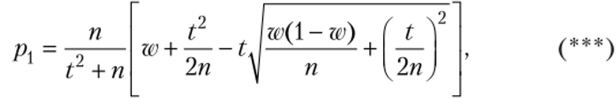
больший корень.

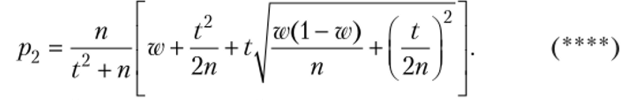
Итак, искомый доверительный интервал р_х<�р< р_г где р_{ и р₂ находят по формулам (***) _и (****).

При выводе мы предположили, что w > р; тот же результат получим при w

Пример. Производят независимые испытания с одинаковой, но неизвестной вероятностью р появления события, А в каждом испытании. Найти доверительный интервал для оценки вероятностир с надежностью 0,95, если в 80 испытаниях событие Л появилось 16 раз.

Р е ш е н и е. По условию, п = 80, т = 16, у=0,95. Найдем относительную частоту появления события А:

w — т/п — 16/80 = 0,2.

Найдем t из соотношения Ф (?) = у/2 = 0,95/2 = 0,475; по таблице функции Лапласа (см. приложение 2) находим t = 1,96.

Подставив п = 80, w = 0,2, t = 1,96 в формулы (***) и (****), получим соответственно р_] = 0,128, р₂ = 0,299.

Итак, искомый доверительный интервал 0,128 <�р< 0,299.

Замечание 1. При больших значения п (порядка сотен) слагаемые t²/(2n) и (t/(2n))² очень малы и множитель n/(t² + п) —1, поэтому можно принять в качестве приближенных границ доверительного интервала.

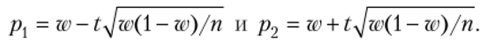
Замечание 2. Чтобы избежать расчетов концов доверительных интервалов, можно использовать табл. 28 книги: Янко Я. Математикостатистические таблицы. М.: Госстатиздат, 1961.

• [1] Напомним, что случайные величины обозначают прописными, а их возможныезначения — строчными буквами. В различных опытах число т появлений событиябудет изменяться и поэтому является случайной величиной М. Однако, поскольку через М уже обозначено математическое ожидание, мы сохраним для случайногочисла появлений события обозначение т.