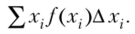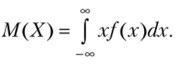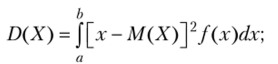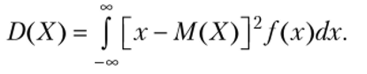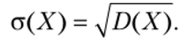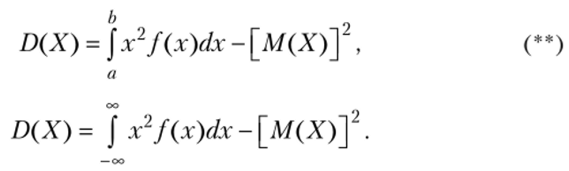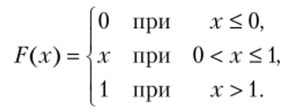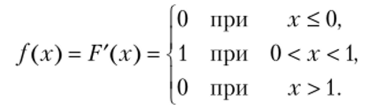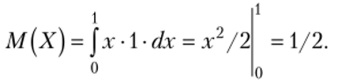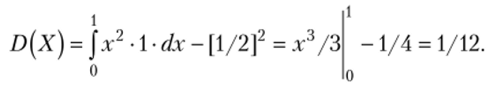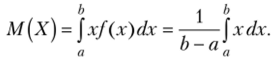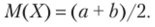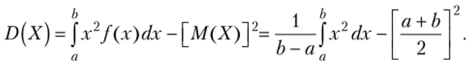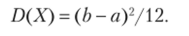Нормальное распределение. 
Теория вероятностей и математическая статистика

Числовые характеристики непрерывных случайных величин

Распространим определения числовых характеристик дискретных величин на величины непрерывные. Начнем с математического ожидания.

§ 1. Числовые характеристики непрерывных случайных величин 125.

Пусть непрерывная случайная величина X задана плотностью распределения f{x). Допустим, что все возможные значения X принадлежат отрезку а, Ь. Разобьем это отрезок на п частичных отрезков длиной Дх₍, Дх₉, …, Дх" и выберем в каждом из них произвольную точку х. (г =1,2,…, п). Нам надо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений х_;. на вероятности попадания их в интервал Дх (напомним, что произведение f (x)Ах приближенно равно вероятности попадания X в интервал Дх):

Перейдя к пределу при стремлении к нулю длины наибольшего из.

ь

частичных отрезков, получим определенный интеграл ~xf (x)dx.

а

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку а, Ь, называют определенный интеграл.

Если возможные значения принадлежат всей оси Ох, то.

Предполагается, что несобственный интеграл сходится абсолютно, т. е. существует интеграл J |х| f (x)dx. Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к-а верхнего — к + °°.

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку а, Ь, то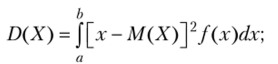

если возможные значения принадлежат всей оси х, то.

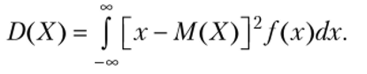
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством.

Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:

Пример 1. Найти математическое ожидание и дисперсию случайной величины X, заданной функцией распределения.

Решение. Найдем плотность распределения:

Найдем математическое ожидание по формуле (*):

Найдем дисперсию по формуле (**):

Пример 2. Найти математическое ожидание и дисперсию непрерывной случайной величины X, распределенной равномерно в интервале (а, 6).

Решение. Найдем математическое ожидание X по формуле (*), учитывая, что плотность равномерного распределения f (x) = 1/(6 — а) (см. гл. 11, § 6):

Выполнив элементарные выкладки, получим 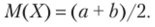Найдем дисперсию X по формуле (**):

Выполнив элементарные выкладки, получим.

Замечание 3. Математическое ожидание и дисперсия случайной величины R, распределенной равномерно в интервале (0,1), т. е. если а = 0, 6=1, как следует из примера 2, соответственно равны M® = ½, D® = = 1/12. Этот же результат мы получили в примере 1 по заданной функции распределения случайной величины R.