Изучение основных понятий теории вероятностей

Фундаментальными понятиями теории вероятностей являются понятия «событие», «вероятность» и «случайная величина».

В теории вероятностей понятие «событие» неразрывно связано с теоретико-множественными представлениями. По определению, под событием понимается любое подмножество множества элементарных исходов. Наиболее предпочтительным при изучении основных понятий теории вероятностей представляется логически обусловленный путь — на базе необходимых понятий теории множеств вводятся основные понятия теории вероятностей.

Изучение понятия «событие» сопряжено у учащихся с трудностями психологического характера. Его ученики обычно воспринимают в контексте бытовой лексики, связывая его с неким единичным бытовым актом, локализованным в пространстве и времени. В соответствии же с определением понятия «событие» наряду с единичным актом надо мыслить и некоторое их множество, числом элементов большим или равным единице, равным нулю. Далее, необходимо четко разграничить понятия эксперимента (опыта) Е и события А как некоторого исхода со, благоприятствующего некоторому комплексу условий S. Для учащихся понятия «эксперимент» и «событие» часто совпадают.

Формирование представления о понятии «событие» начинается с рассмотрения простейших вероятностных моделей — подбрасывание игральной кости, извлечение шаров из урны, извлечение карт из колоды, стрельба, но мишени — и формирования на интуитивном уровне понятия элементарного исхода. При этом имеет смысл вводить и изучать основные понятия в историческом контексте, так как при этом не нарушается и логика развертывания теории вероятностей. Следуя Т. Байесу, рассматриваются такие опыты, при каждом испытании которых возможны несовместные и равновозможные исходы. Каждый такой исход называется элементарным исходом, или элементарным событием. На основе рассматриваемых опытов можно ввести понятие «полная группа событий» как множества попарно несовместных и равновозможных элементарных событий. Все эти понятия дают возможность сформулировать определение понятия «событие» и сформировать первичное представление об этом важном понятии теории вероятностей. Естественно, что при изучении этого фундаментального понятия теории вероятностей, как и при типологии событий, уместна конкретно-индуктивная стратегия изучения (от разнообразных примеров через выделение общих закономерностей к формулированию определения понятия).

Еще одним элементом, способствующим формированию понятия «событие», является классификация событий по степени их «объективной возможности реализации». Изучение классификации событий по этому признаку имеет для учеников важное мировоззренческое значение. Оказывается, что в окружающем мире не существует иных событий, кроме достоверных, невозможных и случайных. Здесь же подчеркивается фундаментальный характер понятия «случайное событие» в построении и изучении закономерностей вероятностных моделей окружающего мира. Примеры таких моделей естественным образом привлекаются из школьных дисциплин (физики, химии, географии, биологии, истории, обществоведения, экономики). При этом имеет место реализация межпредметных связей.

Значение классификации по указанному выше признаку определяется еще и тем, что на ее основе осуществляется фактически первый подход к формированию понятия «вероятность». Если попытаться сопоставить с возможностью или невозможностью наступления конкретного события некоторую численную меру, в частности каждому достоверному событию поставить в соответствие число 1, а каждому невозможному — число 0, тогда понятно, что каждому случайному событию будет соответствовать действительное число из интервала (0; 1). Оставляя временно нераскрытым вопрос о методах установления соответствия между случайными событиями и элементами множества I = (0; 1), логически обоснованно перейдем к изучению вопроса об операциях над событиями.

При изучении этого понятия целесообразно предварительно рассмотреть понятие «отношения между событиями» — имеется в виду отношение включения (А, а В), синонимичное с наиболее часто употребляемыми оборотами речи «событие А влечет за собой событие В», «событие В является следствием события Л», «событие А является частью события В». На основе этого отношения логично ввести определение равных событий (события Л и В называются равными, если Л с В и В с Л). При изучении отношений и операций над событиями естественно использование наглядно-графических средств, которыми являются диаграммы Эйлера — Венна.

В курсе теории вероятностей изучаются следующие операции над событиями — сложение (объединение), умножение (пересечение). Разность событий можно ввести через соответствующее определение или на основе введенных операций (АВ = А и В). Подчеркивая, что события — это множества, можно изучать операции над событиями аналогично изучению операций над множествами, используя примеры, построенные на базе основных вероятностных моделей.

Наличие у учащихся теоретико-множественных представлений позволит им проследить полную аналогию между операциями над множествами и операциями над событиями. Теория вероятностей дает возможность ученикам увидеть, что объекты и отношения в этом разделе математики фактически те же, что и в теории множеств. Разница заключается лишь в терминологии, языке, используемом в теории вероятностей. Полезно составить таблицу соответствия между терминами теории множеств и терминами теории вероятностей.

Следует отметить, что уверенное владение учащимися навыками по работе с операциями над событиями и умение использовать основные свойства этих операций важны для развития навыков решения задач по курсу теории вероятностей. Одна из важнейших проблем, рассматриваемая в теории вероятностей, — определение вероятности сложных событий, получаемых из простых с использованием операций над событиями. Кроме этого, изучение операций над событиями актуально для случаев, когда вероятностное пространство имеет достаточно большое число элементов и решение задач с его использованием приводит к громоздким вычислениям. Эти положения можно считать основой мотивации изучения операций над событиями.

Утверждения относительно свойств операций над событиями, сформулированные в алгебре событий, полностью аналогичны утверждениям алгебры множеств. Это обстоятельство позволяет применить метод аналогий в обучении. Ставя в соответствие невозможному событию пустое множество 0, а достоверному — все множество возможных исходов U (или в других обозначениях О), получается возможность сформулировать теоретико-множественные тождества на языке теории вероятностей. Интересным представляется обсуждение утверждений алгебры событий относительно операций с невозможными и достоверными событиями. Например, для любого события А верны равенства A u U = ?/, A n U = Л, Лп0 = 0, ЛпЛ=Л, Ли0 = 0, ЛиЛ=Л, ЛпЛ = 0, ЛиЛ = (/ и т. д. Желательно проиллюстрировать доказательства этих утверждений наглядно-графическим способом и привести содержательные примеры. Кроме этих соотношений в качестве упражнения можно предложить учащимся подумать, что будет результатом в следующих выражениях: [/п0,Ли0, t/, 0U и т. д.

Методической проблемой при изучении этой темы в процессе решения задач можно считать обучение процедуре выделения простых событий. Разрешение этой проблемы приходит в результате накопления опыта решения задач.

Отбор системы задач по этой теме желательно осуществить так, чтобы позже использовать их для решения задач по вычислению вероятности сложного события по известным вероятностям простых событий.

Изучение операций над событиями необходимо сопровождать примерами, которые достаточно наглядно отражают не только сущность самой изучаемой операции, но и различие в этих операциях. Как правило, ученики достаточно легко построят и сумму, и произведение событий по определению. Труднее сформировать понимание сущности операций над событиями. Например, после введения определений операций суммы и произведения событий и рассмотрения соответствующих примеров можно предложить ученикам следующие задания.

Для обучения выделению простых событий (элементарных исходов) могут быть использованы, в частности, следующие задания.

Задача 22.7.

Бросают два игральных кубика. Какие исходы возможны? Каково общее число исходов? Каково число исходов, в которых в сумме выпало 7 очков?

Задача 22.8.

В лотерее установлены выигрыши по 2000 руб., выигрыши по 1000 руб., выигрыши, но 250 руб. и выигрыши, но 50 руб. Человек покупает 1 билет. Из каких простых событий состоит событие: человек выиграет не менее 250 руб.

Работая с этой задачей, следует обратить внимание и на противоположное событие: выигрыш менее 250 руб. В дальнейшем переход к противоположному событию может упростить вычисление вероятности событий.

Задача 22.9.

В ящике 3 белых и 4 красных шара. Событие состоит в том, что подряд вынимают два шара. Какие исходы возможны? Каково общее число исходов? Каково число случаев появления двух белых шаров, двух разноцветных шаров, непоявления двух красных шаров?

Изученные операции над событиями должны привести к более глубокому осмыслению учащимися таких понятий, как «пространство элементарных событий», «несовместные события», «достоверные события», «невозможные события», «противоположные события», так как эти понятия могут быть определены на основе операции над событиями.

Более сложным является следующее задание (задача 22.10), сюжет которой иллюстрирует одну из причин возникновения и развития теории вероятностей — предварительная оценка результатов и планирование военных действий. Подобные сюжеты характерны для курса теории вероятности в высшей школе. Знакомство с ним облегчит выпускникам изучение этого раздела в вузе.

Задача 22.10.

По самолету стреляют два зенитно-ракетных комплекса (ЗРК). Самолет сбит, когда в него попал хотя бы один снаряд неважно какого ЗРК, первого или второго (и совсем необязательно, чтобы в самолет попали оба ЗРК). Пусть событие А — самолет сбит первым ЗРК, событие В — самолет сбит вторым ЗРК. Событие С — самолет сбит. Ставя перед учениками вопрос, что представляет собой событие С, учитель активизирует деятельность учащихся. Эта задача приводит учеников к рассуждению о возможности интерпретации события С как суммы событий А и В (С = А + В) и возможности представления события С как произведения событий А и В (С = А • В). Для учащихся очевидно, что в качестве решения задачи прежде всего является именно сумма событий, а не их произведение, так как есть четкое понимание того, что самолет будет сбит в случае, когда хотя бы один ЗРК в него попал. Кроме этого, интуитивно понятно, что «вероятность» произведения событий — «что-то из области фантастики», т. е. вероятность события, что в самолет попадут оба ЗРК, много меньше, чем вероятность попадания в него каждым ЗРК в отдельности.

Интересным дополнением к материалу темы является знакомство учеников с законами де Моргана: А п В = А и В, А и В = А п В, справедливость которых может быть проиллюстрирована диаграммами Эйлера — Венна. Эти законы могут быть использованы при изучении, например, противоположных событий.

Второе фундаментальное понятие теории вероятностей — понятие «вероятность». Это понятие является основой построения всех схем вероятностного характера, описывающих широкий класс случайных явлений. Формирование этого понятия, так же как и понятия «событие», начинается с преодоления противоречия между субъектным опытом ученика употребления им термина «вероятность» в повседневной практике и смыслом, вкладываемым в определение этого понятия в прикладной математике.

В настоящее время существует несколько подходов к определению понятия «вероятность события» — статистическое, аксиоматическое, классическое, субъективное (на основе экспертных оценок). Можно сказать, что формирование понятия «вероятность» происходит и в настоящее время. Философский подход к определению вероятности как «меры объективной возможности наступления (или ненаступления) некоторого события» для математики нои аддитивности;

неприемлем в силу весьма его размытого характера. Неприемлемо это определение и для реализации целей обучения теории вероятностей в школьном курсе математики.

В теории вероятностей наиболее распространенной логической схемой построения основ этого раздела является схема, предложенная академиком А. Н. Колмогоровым в 1933 г. Напомним ее.

Пусть имеется произвольное множество Q — пространство элементарных событий некоторого стохастического эксперимента Е и в Q выделена система подмножеств F — событий, являющихся а-алгеброй. Важнейшим свойством ст-алгебры является свойство замкнутости относительно операций п, и,, операция и может быть применена счетное число раз. Для любого А из F определяется числовая функция Р (А), называемая вероятностью события А. Эта функция Р (А) должна удовлетворять следующей системе аксиом:

• • Vg,/e F;
• • Р (Л) >0, Л С F;
• • Р (П) = 1;
• • если А_а (а € /, / — конечное или счетное множество) — непе-

/ л ресекающиеся множества, то Р J А_а =^Р (А_0С) — аксиома СЧеТ;

^а е / у, а е /.

• функция Р (А) определена для любых подмножеств множества нулевой вероятности: если для А, а С1 определена Р (А), причем Р (А) = 0, а В — любое множество, входящее в А (даже, возможно, и не принадлежащее F), тогда Р (В) = 0 — аксиома полноты.

Тройка (Q, F, Р), как известно, называется вероятностным пространством.

Формирование понятия «вероятность» может быть осуществлено в несколько этапов. Сначала, реализуя принцип историзма в обучении, рассматривается классическое определение понятия вероятности.

Вероятностью события А называется отношение числа т случаев, благоприятствующих событию А, к общему числу исходов п:

Р (А) = -. п

Это определение, являясь конструктивным, дает способ вычисления вероятности события и формулируется для так называемых классических экспериментов. Эксперимент называется классическим, если в результате его проведения реализуется множество событий, удовлетворяющих следующим условиям:

• • все события равновозможны;
• • они попарно несовместны;
• • образуют полную группу событий.

Исторически такие события назывались шансами, случаями, исходами, и речь о них шла в рассматриваемых ранее основных вероятностных моделях — подбрасывание игральной кости, извлечение шаров из урны, извлечение карт из колоды, стрельба по мишени.

Можно проверить, что введенное таким образом определение вероятности обладает следующими свойствами:

• • P (U) = 1 — вероятность достоверного события равна 1, так как т = п;
• • Р (0) = 0 — вероятность невозможного события равна 0, так как т = 0;
• • 0 < Р (А) < 1 — вероятность принимает значения из промежутка (0; 1); так как всегда т > 0, т < п, п * 0, то из 0 < т < п следует

_Л т п 0< - < п п

• Р (Л + В) = Р (Л) + Р (В), если события Ли В несовместны.

Это свойство можно обосновать. Пусть в результате проведения серии п экспериментов событие А произошло т_{ раз, а событие В — т₂. Так как события А и В несовместны, то сумма событий произошла т_х + т₂ раз. Тогда получаем, что.

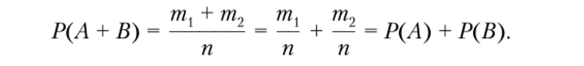
В качестве примеров определения вероятностей событий на основе классического определения вероятности можно рассмотреть задания на вычисление вероятности выпадения «орла» или «решки» при бросании симметричной монеты, рождения мальчика или девочки.

И, например, такое, которое используется в дальнейшем при изучении теорем сложения. Вычислить вероятность того, что при бросании двух кубиков количество выпавших очков будет кратно трем. Решение каждой задачи начинается с выявления полной группы событий. Можно показать, что полная группа событий Q состоит из 36 элементарных исходов, которые представляют собой упорядоченные пары, т. е. = {(со,; со₂), (со,; со₃),…, (со₍.; со₍.)}, где со, — событие, состоящее в выпадении i очков на одном кубике. Обозначим А — событие, состоящее в выпадении числа очков, кратного трем. Этому событию удовлетворяют элементарные исходы: А = {(со,; со₂), (со₂; со,), (со,; со₅), (со₅; со,), (со₂; со₄), (со₄; со₂), (со₃; со₃), (со₃; со₆), (со₆; со₃), (со₄; со₅), (со₅; со₄), (со₆; со₍.)}. Как видно, число таких исходов равно 12.

12 1.

и искомая вероятность по определению равна Р (А) = — = -.

36 3.

Приведенный пример может етать основой для разработки целой серии упражнений по мотивации изучения и формирования понятия вероятности. Например, определить, вероятность какого события выше: выпадения семи или восьми очков; или вычислить вероятность выпадения числа очков не больше трех и т. д.

Одним из существенных недостатков классического определения вероятности является то, что оно пригодно только для классических экспериментов, которые редко имеют место в повседневной практике. Важно добиться от учащихся четкого понимания того факта, что введенное выше определение вероятности обслуживает весьма узкий класс явлений (в рамках классических экспериментов) и в общем случае оно недостаточно, поэтому возникает необходимость рассмотрения других подходов к определению понятия вероятности. С практической точки зрения одним из наиболее важных является статистический подход к определению понятия «вероятность». Его реализация рассматривается как следующий этап формирования теоретико-вероятностных представлений у учащихся. Освоение статистического определения вероятности важно для последующего его применения в разделах математической статистики для оценки статистических характеристик широкого класса явлений различного характера.

Введение

статистического определения понятия «вероятность» неразрывно связано с изучением понятия «относительная частота события» как отношение числа опытов т> в которых появилось событие А, к общему числу экспериментов п. Эту величину обычно.

т

обозначают v, но можно ее обозначить Р*(А), где Р*(А) = — = v по.

п

определению. Это даст возможность ученикам проследить связь с классическим определением вероятности. Для относительной частоты естественно указать следующие свойства:

• • P*(U) = 1, так как т = п;
• • Р*(0) = 0, так как т = 0;

т п

• 0 < Р*(А) < 1, так как 0 < т < п и 0 < — <

п п

• Р*(А + В) = Р*(А) + Р*(В), если А и В — несовместны.

Эти свойства обосновываются аналогично обоснованиям в классическом определении вероятности.

Рассмотрев понятие относительной частоты и ее свойства, можно перейти к статистическому определению понятия «вероятность» как некоторого числа, около которого колеблется и к которому приближается относительная частота события при увеличении числа опытов. Это число, вероятность события Л, обозначается символом.

т

Р (А). Тогда можно написать Р (А) ~ РА) = —. При этом получает;

п

ся не вероятность, как видно из формулы, а лишь некоторое ее приближение (или «оценка»). Вероятность Р (/1), являясь предельным значением Р*(А) при неограниченном увеличении числа экспериментов, обладает теми же свойствами, что и относительная частота. Рассмотрение этой закономерности позволяет в дальнейшем выйти на один из фундаментальных законов теории вероятностей — закон больших чисел.

Одна из проблем, решаемая в теории вероятностей, связана с определением вероятностей различных событий. Один из подходов к ее решению связан с применением статистического определения вероятности. Это позволяет получить оценки вероятностей событий на основе проведения достаточно больших серий испытаний.

Существует еще одно определение вероятности — определение так называемой геометрической вероятности. Оно применяется в случае, если имеет место эксперимент с бесконечным числом исходов. К таким задачам сводится, например, задача о вероятности попадания брошенной наугад «точки» на некоторую область g, gczG. Определение геометрической вероятности имеет вид: Р (А) = mes g

=-—, где mesg и mesG — меры множеств g и G.

mesG.