Основные вехи истории логики

Как уже неоднократно говорилось, создателем логики как науки был греческий философ Аристотель, и произошло это рубежное для истории человечества событие в IV в. до н.э. Но, безусловно, надо подчеркнуть, что появление логических трактатов великого ученика великого Платона, в которых была поставлена и решена задача создания специальной науки о необходимых нормах мышления, явилось закономерным следствием развития «логической» (в широком смысле этого слова) традиции в древнегреческой философии VI—IV вв. до н.э. О некоторых, наиболее примечательных, с нашей точки зрения, вехах этой традиции мы сейчас и расскажем (следует отметить, что в традиционных учебниках по логике эти интереснейшие вопросы истории человеческого познания мира и самопознания затрагиваются «реже, чем почти никогда»).

Глубокое философское откровение по поводу природы того, что мы сейчас называем процедурой определения, можно отыскать в дошедших до нас фрагментах творчества Анаксимандра из Милета (ок. 610 546 до н.э.). Анализируя вопрос о том, какую природу должно иметь архэ — первоначало, субстанция всего сущего, — Анаксимандр приходит к выводу, что это должно быть нечто Беспредельное, Неограниченное, Бесконечное, по-гречески Апейрон, — ибо только тогда это нечто может лежать в основании всего разнообразия вещей и явлений реального мира. Если любая конечная (а потому конкретная) вещь в итоге берет начало из апейрона (в пределе сводится к нему), значит, апейрон сам не может быть чем-то конкретным, ограниченным, определенным. Но не следует трактовать апейрон как некое начало, обладающее свойством «беспредельности». Апейрон — это скорее сама беспредельность и неограниченность. И тогда — внимание, самая соль рассуждения Анаксимандра! — возникновение тех или иных вещей в бытии, определение их в качестве таковых (кошек, столов, мужественных поступков и т. д.) есть их опредёливание по отношению к изначальной беспредельности. Ведь описать вещь в качестве какой-то конкретной — значит, указать свойства, которыми эта вещь обладает (тем самым будут отброшены свойства, которыми она не обладает), т. е. провести замкнутую границу внутри бесконечного множества возможных свойств. Все, что окажется внутри этой границы (точнее, все носители свойств внутри этой границы), будет относиться к классу данных вещей, все, что вне ее, — будет иными вещами. Таким образом, апейрон (как это самое бесконечное множество свойств и определений) потенциально содержит в себе все вещи.

Иными словами, Анаксимандр впервые в истории человеческой мысли де-факто дал философско-методологический анализ логической процедуре определения, трактуя ее, правда, сугубо в онтологическом ключе, т. е. показал связь между этой процедурой и возникновением самих этих вещей в реальности в качестве, по крайней мере, объектов возможного рассмотрения. Ведь то, что мы называем вещами, может быть более чем разнообразным по своим свойствам — но оно обязательно будет «каким-то». Опираясь, в частности, и на это открытие Анаксимандра, великий Платон позже построит грандиозную модель бытия, о которой мы уже говорили.

Представители так называемой Элейской философской школы (по названию города Элея в Южной Италии) — главным образом Парменид (вторая половина V — первая половина IV вв. до н.э.) и его ученик Зенон Элейский — были первыми, кто стал в своем дискурсе использовать строгие последовательные рассуждения-доказательства, кто обратил внимание на необходимость использования общих отвлеченных понятий и категорий при обосновании тех или иных моделей мироздания.

Среди философов широко известно рассуждение Парменида: «Небытия нет. А нет его потому, что оно немыслимо (видимо, древнегреческий мыслитель опирается на неявный аргумент: „Если нечто есть, о нем можно помыслить“. — К. М.). А немыслимо оно потому, что всякая попытка мыслить его сразу же сделала бы его бытием — по крайней мере, в качестве предмета этой мысли. Следовательно, подлинное бытие как таковое и мышление о нем совпадают! Предмет мысли и мысль о предмете в данном случае тождественны» (такая философская доктрина называется сейчас панлогизмом).

Зенон Элейский (ок. 490 — 430 до н.э.).

Зенон же прославился тем, что сформулировал множество рассуждений, названных апориями (от греч. «затруднительная, безвыходная ситуация»), в которых обосновывал мысль своего учителя о том, что изменчивый чувственно воспринимаемый мир нельзя адекватно отразить силой разума, используя строгие, четкие, непротиворечивые и однозначные понятия. Вот, к примеру, его знаменитая апория «Летящая стрела».

Представим себе летящую в воздухе стрелу. В каждый момент времени она занимает определенное место в пространстве. Но это значит, что она там в этот момент времени покоится (иначе бы ее там не было, она бы не «занимала» «этого места»). Но так как это справедливо для любого момента времени и для любого места, получается, что летящая стрела покоится. Мы пришли к противоречию. Следовательно, необходимо сделать вывод, что отразить движение в понятиях разума невозможно. Движение, конечно, есть (в чувственном мире, «мире мнения», как его называли элеаты), но его нельзя сделать предметом мысли, следовательно, элементом теоретической модели мира, претендующей на отражение его сущности.

Многие из наших читателей, без сомнения, слышали и о парадоксе (апории) Зенона под названием «Ахиллес и черепаха». На прямой дороге в 1000 м друг от друга (в точках А и В соответственно, рис. 1.7) находятся самый быстрый бегун Греции Ахиллес и самое медлительное существо черепаха. Они одновременно начинают движение в одном направлении, причем Ахиллес передвигается со скоростью, в сто раз (считаем так для удобства) превышающей скорость черепахи.

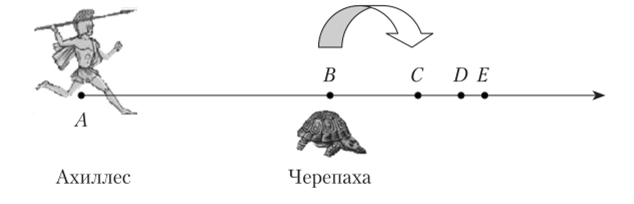
Рис. 1.7. Ахиллес и черепаха на старте.

Когда Ахиллес добежит до того места, где была черепаха в момент «начала соревнования», ее там уже, конечно, не окажется, ибо она успеет отползти на 10 м (рис. 1.8, без соблюдения масштаба).

Рис. 1.8. Ахиллес и черепаха: догонит или не догонит?

Но когда Ахиллес преодолеет эти 10 м, черепаха по-прежнему будет впереди него — теперь на 10 см (в точке D). Пока Ахиллес ликвидирует это отставание, черепаха создаст себе новую фору — пусть совсем ничтожную, всего в один миллиметр, но все же «фору» (переползет в точку Е). И такая ситуация будет бесконечно повторяться. За то время, пока Ахиллес преодолевает оставшийся с «предыдущего раза» «кусок дистанции», отделяющий его от черепахи, эта черепаха успевает создать себе новый «запас», который, как бы мал он ни был, никогда не будет равным нулю. Следовательно, хотя в реальной жизни Ахиллес, конечно, и догонит, и перегонит черепаху, построить непротиворечивое логическое объяснение этого факта, полагает Зенон, оказывается невозможным¹.

Вот третья (рис. 1.9) из знаменитой четверки апорий Зенона против возможности непротиворечиво мыслить движение — апория «Дихотомия» («деление надвое»).

Рис. 1.9. Апория «Дихотомия».

¹ См. неплохую анимацию по ссылке: URL: http://nibiryukov.narod.ru/nb_russian/nbr_ teaching/nbr_teach_ppp/nbr_ppp_osnovy_filosofii/nbr_zeno.ppt (слайды 22—39), здесь же содержится отличное изложение четвертой из основных апорий Зенона, а также ряда других.

Неподвижное тело находится в точке А (например, учитель сидит в классе за своим столом). Чтобы достичь точки В (входной двери, т. е. чтобы выйти из класса), это тело сперва должно пройти половину расстояния АВ, т. е. достичь точки С. Но чтобы достичь точки С, предварительно надо достичь точки D (AD = DC). Чтобы достичь точки Д надо перед этим достичь точки Е (АЕ = ED) — и так до бесконечности. Следовательно, движение не может начаться (и закончиться, если оно уже происходит). Учитель никогда не сможет выйти из класса. Разумеется, не в реальном чувственном мире, а в мире понятий, т. е. никогда не сможет объяснить, как именно ему удалось это сделать (выйти из класса).

А вот сформулированный Зеноном парадокс уже другого вида. Одно падающее зерно не производит никакого шума. (И даже если мы добавим второе зерно, шума тоже не возникнет.) Так почему производят шум тысячи падающих зерен?

V—IV вв. до н.э. в истории Древней Греции — эпоха «высокой классики», эпоха расцвета греческой культуры в целом и ее основных сфер (искусства, философии, науки). Это эпоха «греческого Просвещения». И огромную роль в этой эпохе в частности и в истории человеческой мысли вообще (прежде всего — в логике) сыграли так называемые софисты.

Софисты (от греч. софистес — мудрец¹) — платные преподаватели ораторского искусства и риторики прежде всего, а также прочих, как сейчас сказали бы, «общегуманитарных» дисциплин. Повсеместное распространение в Греции в V в. до н.э. подобных учебных центров для богатых граждан объяснялось весьма просто. Развитие полисной демократии вело к повышению социального авторитета «публичных профессий» (политических деятелей различного ранга — от судей и «народных заседателей» до военных стратегов), овладение которыми с необходимостью предполагало недюжинный ораторский талант. Это уже не говоря о том, как с этим талантом непосредственно был связан реальный престиж в обществе у соответствующего «профессионала». А спрос, как известно, рождает предложение. Умение разумно выстраивать свои мысли и грамотно их излагать всегда ценилось очень высоко в по-настоящему культурном и просвещенном обществе, а в такой социальной структуре, как греческое общество того периода, — и подавно. «В античной традиции на первое место входит агонистика — состязательность, проникающая буквально во все сферы общественной жизни. К числу существенных отличий полисной культуры следует отнести активную правовую практику. В V в. в Афинах каждый гражданин имел право выдвигать собственный законопроект и обсуждать другие проекты»^[1][2]. Таким образом, «первоначально логика разрабатывалась в связи с запросами прежде всего практики судопроизводства. От логической доказательности речи обвиняемого, обвинителя, адвоката, других участников прений часто зависело решение суда — особенно в сложных и запутанных ситуациях. Неумение четко и ясно формулировать свои мысли, изобличать подвохи и „ловушки“ своих оппонентов могло стоить оратору очень дорого»¹.

Протагор, знаменитый софист (ок. 490 — 420 до н.э.).

Но, безусловно, позитивная роль, заключавшаяся в безусловном повышении общего уровня гуманитарной культуры в Греции, довольно быстро отошла у софистов на второй план. Чем более престижными и доходными становились соответствующие должности, тем менее разборчивыми становились претенденты на них^[3][4]. И тем менее разборчивыми становились, естественно, и учителя, ибо «цель оправдывает средства». И уже оказывалось неважным, каким именно путем был устранен конкурент на глазах народного собрания — путем грамотного переубеждения и объективного доказательства своей правоты (т.е. в рамках честного спора ради истины, где, если и побеждает, то побеждает объективно более знающий и достойный) или просто путем демонстрации неспособности оппонента успешно вести «словесный поединок» (спор ради победы), недостаточности его риторической культуры, т. е. якобы образованности. Софисты обучали своих слушателей разного рода «хитрым» приемам (получившим название софизмов), которые позволяли в споре:

• 1) сбить с толку не подготовленного к такой атаке собеседника;
• 2) выставить его в глазах судей простофилей, который даже «сам не понимает, что он утверждает»;
• 3) завладеть инициативой в диалоге (например, в рамках публичных «дебатов конкурентов» — претендентов на какую-либо важную должность);
• 4) выиграть дело.

Эти приемы, как правило, явно или неявно нарушали известные сейчас каждому образованному человеку законы логики и принципы ведения спора ради истины. Примечательность ситуации состояла в том, что указать софистам тогда на их алогичность было невозможно по весьма прозаической причине — сама логика как систематическая наука о правилах рассуждений еще не была создана (это сделает Аристотель лишь в следующем веке). Софисты, рекламируя себя, беззастенчиво утверждали, что они могут доказать «все что угодно». Иными словами, «все, что нужно сделать истинным, можно считать таковым и поэтому сделать таковым, необходимо лишь умение аргументировать». А за последнее в таком разрезе действительно можно было и платить немалые деньги «сэнсэям». Философские основания идей софистов восходят к знаменитому утверждению главного из них — Протагора: «Человек есть мера всех вещей — существующих в их существовании и не существующих в их несуществовании». Иными словами, как кому кажется, так оно и есть. Рассказывают, что софисты достигали такого риторического мастерства, что могли в течение одного выступления сначала совершенно убедить аудиторию в верности одной точки зрения, а потом не менее впечатляюще — в верности противоположной.

На следующих схемах-рисунках приведены некоторые из самых известных софизмов.

А на мотив знаменитого софизма «Покрытый» (пожалуй, одного из самых тонких и философских среди всех) нами в рамках нашего проекта по популяризации логики была написана следующая небольшая «пьеса».

Агамемнон и сын его Орест, или Женская логика в Древней Греции.

{логическая интермедия без пролога и эпилога)

Действующие лица и исполнители: Агамемнон, сын его Орест, дочь его Элечка (она же Электра), козни Клитемнестры, кинорежиссер Александр Серый, Эсхил, дух К. А. Михайлова (последние четыре персонажа прямого участия в действии не принимают).

Агамемнон {обращаясь к Электре, указывая на стоящего рядом субъекта, закутанного в покрывало). Вот видишь этого человека под покрывалом?

Электра. Да, отец.

Агамемнон. Знаешь ли ты, кто это?

Электра. Нет, падре, как же я могу его знать, раз я его не вижу?

Агамемнон. Ты же сказала, что видишь?

Электра {путаясь в показаниях). Ну… я вижу… но не вижу.

Агамемнон {снисходительно улыбаясь). Это как же так, о возлюбленная дочь моя?

Электра {оживляясь от посетившей ее конструктивной идеи). Я не вижу, кто там. Поэтому не знаю этого человека.

Агамемнон (довольно усмехаясь). Отлично, Элечка! {Обращаясь к человеку под покрывалом.) Орест, можно заканчивать маскарад!

Человек сбрасывает покрывало, и все видят, что это Орест. Электра в шоке.

Агамемнон. Электра, ты знаешь этого человека?

Электра (растерянно). Да… это же мой браг Орест. Привет, Орик! Как ты здесь оказался?

Агамемнон (злорадно потирает руки). Вот это и называется женская логика… Сначала сказала, что не знает этого человека, а потом выяснилось, что отлично знает — ведь не может же она не знать своего брага! Это как в том совейском фильме: тут помню, а ту г не помню… Одно слово — женщины… Никакой способности говорить правду! «Правда ли, что Аякс предал греков, сговорившись с Приамом? — Сущая правда, архонт! Только не с Приамом, а с Одиссеем. И не сговорился, а поссорился. И не Аякс, а Паламед. И не предал, а защищал…» Вот и моя Клитемнестрочка что-то замышляет…

С тех самых пор слово «софизм» приобрело явно негативный оттенок: его значением стали заведомо неправильные рассуждения, запрещенные приемы и уловки, которые, однако, нелегко разоблачить сразу. Софизмы могут быть основаны на подмене понятий, на смешении логических отношений противоположности и противоречия, на двусмысленности выражений, на «обыгрывании» сложного диалектического характера процесса познания, на ложных аргументах, которые только кажутся истинными, и т. д. (Попробуйте самостоятельно опровергнуть приведенные в этом параграфе софизмы.) Позднее Аристотель с присущей ему педантичностью систематизировал и разоблачил софистические приемы в своем блестящем сочинении «О софистических опровержениях».

Недоумение Отец, глядя в тетрадь сына-школьника: «Я что-то не пойму: здесь написано „Классная работа“, а стоит почему-то двойка» (отличная подборка подобных примеров здесь: URL: http://shopwork.ru/work-1987/ и URL: http://window.edu.ru/library/ pdf2txt/314/77 314/58408/ pagc4).

Обратите внимание на следующую разницу. «Внешне правильное рассуждение, содержащее какую-то скрытую уловку, называется софизмом. Внешне правильное рассуждение, содержащее скрытую неумышленную ошибку (допущенную, например, по недостатку логической культуры или случайно), называется паралогизмом. Строгое рассуждение, которое с логической неизбежностью приводит к противоречию в силу внутренней противоречивости используемой теории (или заданных условий), называется парадоксом"'. О парадоксах подробно пойдет речь в следующей главе.

Выполните упражнения 9—10 из Практикума.

«Софизмы прямо ставили вопрос о необходимости построения строгой логической теории. Обнаружилась явная проблема сущности доказательства как процедуры. Нарушая еще не открытые законы логики, софисты непосредственно подвели древнегреческую мысль к их формулированию. Таким образом, особая наука логика возникла еще и как в определенном смысле теоретическое оправдание здравого смысла, интуитивного понятия доказательства» (А. А. Ивин).

Но ни в коем случае не следует трактовать деятельность софистов как сугубо деструктивную. Они «разбудили» мысль, учили людей думать, сравнивать, обсуждать сложные неоднозначные вопросы, обосновывать свою позицию; показали, что в большинстве гуманитарных проблем альтернативные позиции могут опираться па разумные и сильные аргументы каждая. Софисты внесли большой вклад в становление риторики и теории аргументации, фактически именно они разработали очень сильный методический прием в риторике — «вызываю огонь на себя» (сначала демонстративно полемизировать против самих себя, а потом разбивать эту критику заранее подготовленными аргументами), учили видеть сильные стороны любой позиции. Их роль в греческом Просвещении была весьма значительной.

Однако релятивизм (учение о том, что все относительно) софистов, их критика объективности истины, их эпатажность противоречили духу греческого миросозерцания (основанного на понятиях меры, гармонии, порядка, калокагагии — тождества между истиной, добром и красотой) и вызвали резкую критику со стороны «традиционалистов», во главе которых встал Сократ (469—399 до н.э.), дело которого продолжил его ученик Платон.

Сократ и Платон окончательно утвердили понимание различий между единичным и общим, внесли огромный вклад в искусство диалектики как^[5]

отыскания истины в споре, как методики сопоставления разнообразных позиций по обсуждаемому вопросу и выработки решения-консенсуса, как бы мы сейчас сказали. Прославился Платон в логике и своими знаменитыми пятью доказательствами бессмертия души, два из которых — кажущихся нам наиболее примечательными с точки зрения логики как теории рассуждений — мы сейчас здесь приведем.

Довод от взаимоперехода противоположностей.

В мире мы наблюдаем постоянные переходы противоположностей друг в друга, сохраняющие гармонию мира. Теплое.

остывает и становится холодным, которое, нагреваясь, снова становится теплым. Сон и бодрствование, болезнь и здоровье постоянно сменяют друг друга. Живое умирает и становится мертвым. Если бы не было обратного перехода («оживления» неживого), все рано или поздно стало бы мертвым (Платон неявно полагает, что мы не можем сделать заключения, что мир имел начало, количество живого в нем постоянно уменьшается, а мы сейчас просто живем в момент, когда «живое еще сохраняется».) Но этого не наблюдается. Поэтому необходимо должно существовать начало, отвечающее за обратный переход — из неживого в живое, причем начало бессмертное. А это начало и есть душа. Устами Сократа Платон говорит: «Души умерших должны существовать в каком-то месте, откуда они вновь возвращаются к жизни»^[6]. «Взаимопереход противоположностей осуществляется здесь как космический круговорот душ» ^[7].

Довод от постоянства душ как таковых. Все души постоянны как души. Хотя они между собой и различны, но «быть душой» для всех душ одинаково и неизменно. А все неизменное бессмертно как таковое, т. е. этот принцип души бессмертен. Но душа как нечто нематериальное есть то, что полностью воплощает принцип «быть душой». Поэтому бессмертна и сама душа.

Подумайте, как можно возразить Платону на эти доводы.

«И хотя в процессе аргументации умение разоблачать различного рода софизмы необходимо, но все же оно является недостаточным. Особенно если речь идет о научной аргументации, целью которой является не победа в споре, а отыскание истины. Быстро развивавшаяся античная наука была вторым важным источником возникновения логики. В рамках философии, физики, геометрии, биологии постепенно вырабатывались самые разнообразные познавательные приемы, которые нужно было методологически обосновать, обобщить и систематизировать. Этим занимались многие мыслители, но как стройная научная теория — подчеркнем это еще раз — логика впервые сформировалась во второй половине IV в. до н.э. в трудах выдающегося древнегреческого философа Аристотеля. Логические трактаты Аристотеля — „Категории“, „Об истолковании“, так называемые Первая и Вторая „Аналитики“, „Топика“ и „О софистических рассуждениях“ — были в I в. н.э. объединены его последователями под общим названием „Органон“. Слово „органон“ по-гречески означает „орудие“, и для самого Аристотеля логика выступает прежде всего как орудие, инструмент любого рационального познания. С другой стороны, аристотелевскую логику часто называют „каноном“, т. е. правилом, образцом. Она не только объясняет, как должна строиться любая наука, но и сама является примером строгой научности и рациональности. Примечательно, что логическая система Аристотеля является первой в истории человечества формальной аксиоматической теорией — идеал, к которому стремятся все точные науки»^[8].

Полезный совет Любой экспромт должен быть тщательно подготовлен.

Обобщим наши знания о сложившихся к середине IV в. до н.э. объективных предпосылках возникновения логики.

• 1. Математическая практика (осуществление различного рода математических доказательств). Появлялись различные тины доказательств (например, от противного). Возникала необходимость их обоснования.
• 2. Научная практика.
• 3. Общественно-политическая практика (судебное и политическое красноречие), широкое распространение интеллектуальных споров. Стало необходимым осуществлять обоснование мыслей. Требовал ответа вопрос: «Что считать доказанным?»
• 4. Высокая степень разработанности собственно философского знания. Необходимо было создание инструмента строгих и систематических философских исследований.

Благодаря гению Аристотеля этот «запрос эпохи» был выполнен.

У нас нет возможности подробно рассматривать в этом учебнике историю логики. Заинтересовавшиеся читатели смогут сделать это сами, например, используя книги А. О. Маковельского «История логики», П. С. Попова и Н. И. Стяжкина «Развитие логических идей от Античности до эпохи Возрождения» или И. Н. Грифцовой «Логика как теоретическая и практическая дисциплина» (в которой история логики более чем оригинально и методически продуктивно представлена как смена парадигм различных трактовок «образа логики» как науки). Но несколько слов о «послеаристотелевском пути» развития логики мы все же скажем.

Большой вклад в становление логики как теории рассуждений сыграли представители школы стоиков (эпоха поздней Античности) — они заложили основы теории умозаключений из сложных высказываний (де-факто фрагменты современной логической теории «Логика высказываний», которую мы с вами вскоре начнем изучать).

Средние века (прежде всего — схоластика) — эпоха безраздельного царствия логического авторитета Аристотеля, эпоха комментирования его сочинений, уточнения и детализации его мыслей. В то же время средневековые логики внесли большой вклад в «логическую парадоксологию», учение о «неразрешимых предложениях» (типа «Это предложение ложно»), которые тогда назывались по-латыни инсолюбилиями (об этом см. в гл. 2).

Новое время — эпоха возникновения и бурного развития эмпирической экспериментальной науки — обогатило логику теорией индуктивных рассуждений, так называемой логикой открытия Фр. Бэкона, озаглавившего свой логический трактат весьма претенциозно —.

«Новый Органон» (с аллюзией на отказ от аристотелевской парадигмы логики).

Представители немецкой классической философии И. Кант и Г. Гегель разрабатывали иные варианты реформы логики на путях ее «философизации» и придания ей (в ее новом облике) в той или иной степени содержательного характера. Так, И. Кант, выдвинув^РБэкон проект «трансцендентальной логики», предложил ото- (1о61—1626).

ждествить эту новую логику и теорию познания вообще (параллельно сводя к теории познания и учение о самом бытии).

Г. Гегель же, разработав первую концепцию диалектической логики, фактически отождествил законы мышления (причем не столько индивидуального, сколько Мирового Разума как такового) с законами самого бытия, превратив все мироздание в те или иные формы существования логических законов, категорий и принципов. И Кант, и Гегель пытались дать ответ об источниках и природе логического знания, объяснить его глубинными, философскими принципами устройства бытия и познания.

Георг Гегель, Но еще раньше — уже упо;

Готфрид Лейбниц (1646−1716).

• (1770—1831) минавшимся Г. В. Лейбни-
• — цем — при осмыслении задач

логики как науки был выдвинут принципиальный методологический проект, на протяжении двух с половиной столетий будораживший умы ученых.

«Когда-нибудь наступит такое время, — писал Лейбниц, — когда люди перестанут спорить, а просто сядут и посчитают, кто из них прав». Фактически великий математик и философ имел в виду идеал полной формализации человеческого знания, создание универсального языка, на котором однозначным образом может быть сформулирована вся информация о мире, а также формальной математизированной системы, в которой станет возможным неоспоримо доказать (как в геометрии) все содержательно истинные утверждения о мире, по крайней мере, самую существенную их часть, станет возможным проверить — по аналогии с математическими вычислениями — все рассуждения и обоснования на предмет их соответствия требованиям разума и истины.

Курт Гёдель (1906—1978).

Проект Лейбница действительно был фундаментальным и в течение многих десятилетий находил отклик у многих «формалистов». За два с лишним века математики серьезно продвинулись на пути к осуществлению «замысла Лейбница». Но их ждала катастрофа! В 1931 г. 25-летний (!) великий немецкий математик Курт Гёдель доказал свою знаменитую теорему, согласно которой в любой формальной системе, содержащей элементарную арифметику (утверждения о числах), всегда можно придумать (сконструировать) предложение, которое будет заведомо истинным, но в принципе не доказуемым средствами этой системы. Теорема Гёделя перевернула мировоззрение множества математиков и специалистов по философии математики, став одним из самых ярких событий интеллектуальной жизни всего XX в. (хотя и была «негативным открытием» по своей сути). Гёдель раз и навсегда доказал, что формализация знания (полная) невозможна в принципе, что понятия истинности и доказуемости принципиально невозможно сделать эквивалентными. Из основной теоремы Гёделя следовало несколько других весьма важных утверждений, в частности то, что непротиворечивость математики (т.е. принципиальную невозможность доказать некое утверждение А вместе с его отрицанием) нельзя доказать средствами самой математики, как надеялись многие ученые. Для этого нужно использовать более сильную систему. Но тогда встанет вопрос уже о ее собственной непротиворечивости. А чтобы доказать эту непротиворечивость, нужна еще более сильная система. И так до бесконечности. Оказалось, что самое строгое знание — математическое — в принципе не может быть окончательно обосновано. Крупный математик Герман Вейль обобщил этот печальный для математиков факт следующей сентенцией: «Бог существует, так как математика, несомненно, непротиворечива. Но существует и Дьявол, ибо доказать эту непротиворечивость мы не можем».

Достижения Гёделя (хотя и «ограничительные») на стыке логики и математики отлично демонстрируют суть характерного для XX в. процесса — математизации логики, начало которой положила так называемая революция в логике на рубеже XIX—XX вв. Ее суть можно обобщить в следующих пунктах.

1. Логикой вплотную занялись математики, внедрив в определенные разделы логики точные методы проверки, математический аппарат. Замысел Лейбница в этой своей части окончательно воплотился в жизнь («математизация»). Огромную роль сыграла здесь так называемая булева алгебра, названная так в честь знаменитого математика Д. Буля.

• 2. Э. Гуссерлем был нанесен сокрушительный удар психологизму в логике, что способствовало дальнейшему развитию логики как автономной теоретической науки.
• 3. В рамках строгих теорий (например, теории множеств) были обнаружены парадоксы (см. следующую главу). Это поистине потрясло логикоматематический мир. Осмысление этих парадоксов (не говоря уже о более поздних работах Гёделя и польского математика Альфреда Тарского) дало ценные результаты в области философии математики и логики.
• 4. Появились так называемые неклассические логики — логики, отрицающие те или иные постулаты логики классической (двузначность, экстенсиональность и т. д.), например, трехзначная (а потом и многозначная вообще), интуиционистская, модальная (использующая логические союзы «необходимо, что», «запрещено, чтобы» и т. д.), релевантная и др.

• [1] Как шутит В. В. Горбатов, пользуясь выразительными возможностями русского языка, на деле эти «мудрецы» оказались самыми настоящими мудрилами
• [2] Зайцев Д. В. Теория и практика аргументации. М., 2007. С. 9.
• [3] Горбатов В. В. Логика. М., 2007. С. 13.
• [4] История повторяется, не так ли?
• [5] См.: Горбатов В. В. Указ. соч. С. 13.
• [6] 2 Диалоги Платона. URL: http://www.deir.org/libr/?go=book&id=470&p=429.
• [7] Лосев Л. Ф. Комментарии к диалогам Платона: компиляция из четырехтомного изданиядиалогов Платона (М.: Мысль, 1990—199?). К.: PSYLIB, 2005. URL: https://www.psyoffice.ru/9/losew06/txt 12.html.
• [8] См.: Горбатов В. В. Указ. соч. С. 14.