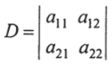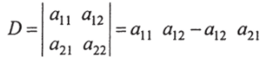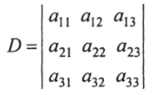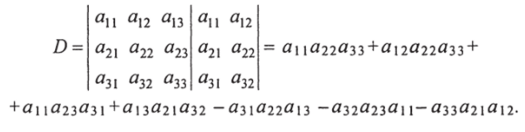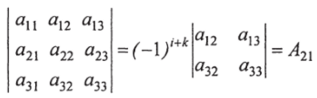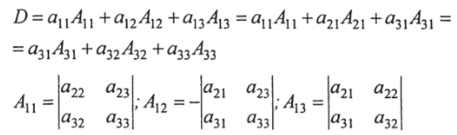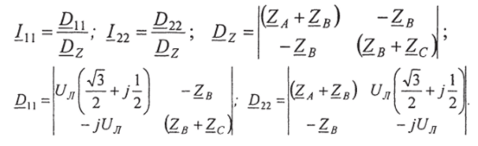Расчет трехфазных электрических цепей с помощью определителей

Определителем второго порядка называется выражение D, образованное из четырех элементов а,*, расположенных в квадратной таблице элементов вида:

Индекс / в обозначении а,* указывает номер строки, в которой находится данное число, а индекс к — номер соответствующего столбца.

Определители второго порядка вычисляются по формуле:

Девять элементов а,*, расположенных в квадратной таблице элементов, образуют определитель третьего порядка вида:

Приписав к элементам определителя третьего порядка справа два первых столбца, можно его вычислить по следующей схеме:

Определитель второго порядка, полученный из определителя третьего порядка вычеркиванием строки (г) и столбца (к), на пересечении которых расположен элемент а,*, носит название минора этого элемента.

Минор элемента а,*, умноженный на (-1)'⁺*, называется алгебраическим дополнением элемента а,* и обозначается через А,_К:

Каждый определитель третьего порядка можно разложить по элементам строки или столбца следующим образом:

ит.д.

Используя это свойство, можно вычислить и определитель четвертого порядка, сведя его к четырем определителям третьего порядка, и т. д.

С учетом уравнений, составленных по второму закону Кирхгофа для контурных токов (где 2г = 2 г 2ъ — ?31 и 2ц = 2п), алгебраические дополнения с теми же индексами также будут равны между собой (И 12 -АгАъ =Ац н Агз =Изг).

Систему уравнений (4.30), составленную для трехфазного потребителя, фазы которого соединены звездой (рис. 4.17), можно решить с помощью определителей. При этом:

Соответственно, система уравнений (4.32), составленная для потребителя, фазы которого соединены треугольником (рис. 4.18), может быть решена исходя из выражений:

Решение определителей более высокого порядка при расчёте задач методом определителей является трудоёмким.

В приложении П1 приведены возможные варианты соединения трехфазных потребителей и их векторные диаграммы.