Основные характеристики одномерных количественных данных

Для того чтобы изучать какие-то переменные и сравнивать их между собой, необходимо уметь рассчитывать основные числовые характеристики признаков.

Характеристики центра группирования данных Средние величины

Средние представляют собой обобщающие показатели, характеризующие центр группирования данных.

Как правило, рассматривают средние: арифметическую, гармоническую и геометрическую.

Вид средней выбирается согласно определяющему свойству: значение определяющей функции ф (лг, х₂,…, х") не изменится, если исходные данные заменить средней.

Пример 4.5.

Фонд оплаты труда п работников х_1з… х" можно представить как^д и как х • п,

i-1.

где х — средняя заработная плата п работников. Тогда 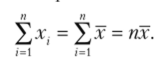Получаем среднюю арифметическую:

Если данные сгруппированы, т. е. заработную плату х_: получают m_t работников,.

к

где 1=1,2…k и п = Yj^mp ^т-^е;

i=i

го получается средняя арифметическая взвешенная

Пример 4.6.

В единицу времени п рабочих изготовляют соответственно х, х₂,…, х" изделий. Определите среднюю производительность труда п рабочих.

Суммарное время изготовления п изделий п рабочими равно:

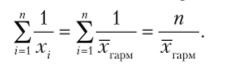
Определяющее правило: суммарное время изготовления рабочими п изделий не изменится, если все х_; заменить на х.

Отсюда получается средняя гармоническая.

Пример 4.7.

Пусть за время пути автомобиль m_t километров проехал со скоростью X/, где /= 1,2,…, k. Определите среднюю скорость автомобиля за все время пути.

Определяющее правило: общее время в пути не изменится, если фактическую скорость X) заменить на среднюю.

Из определяющей функции следует: суммарное время равно:

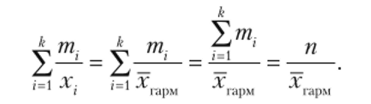
Тогда получается средняя гармоническая взвешенная:

Пусть .г, х₂,…,х" — темпы роста объема производства за п лет, требуется определить средний теми роста.

Определяющее правило: произведение темпов роста не изменится, если все x_it

п и.

х₂,…, х_п заменить па средний темп роста х_птл, т. е. выполняется условие П х. - О «.

<�ж| /=1.

тогда имеет место средняя геометрическая'.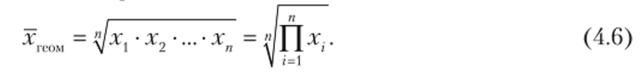

Если данные сгруппированы, то получается средняя геометрическая взвешенная

Средние геометрические используют при анализе временных данных. Из рассмотренных средних наибольшее распространение па практике имеет.

1 ^п

средняя арифметическая х = —^х_г Рассмотрим подробнее ее свойства.

п ы I.

• 1. Средняя арифметическая постоянной величины равна самой постоянной. Пусть Xj = с для всех г = 1,2,…, п. Тогда, подставив с вместо х_{ в формулу средней, легко получим х = Я
• 2. Если ко всем значениям х_х прибавить постоянную с, то средняя арифметическая изменится на эту постоянную, т. е. х + с = х + с.

В самом деле,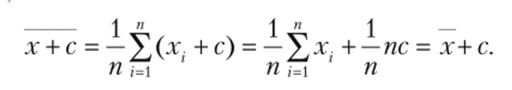

3. Если все значения х_х умножить на постоянную с, то средняя арифметическая изменится в с раз, т. е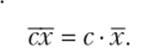

4. Средняя арифметическая от линейной функции равна линейной функции от средней арифметической.

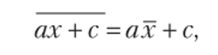
где а и с — постоянные величины. В самом деле,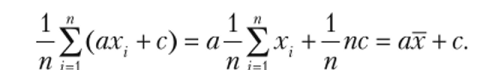

На раскрой каждого из восьми костюмов на фабрике затрачено соответственно 60, 55, 50, 52, 45, 49, 58 и 46 минут. Определите среднюю арифметическую.

Среднее арифметическое для несгруппированных данных вычисляется по формуле (4.2):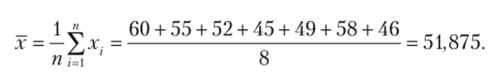

Пример 4.10.

Па основе интервального вариационного объема производства предприятий легкой промышленности, представленного в таблице ниже, вычислите среднее арифметическое.

Среднее арифметическое для сгруппированных данных — интервального ряда — вычисляется, но (4.3):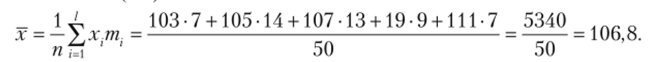

Другие характеристики центра группирования Медиана — знамение признака, приходящегося на середину вариационного ряда.

Например, при п = 5 имеем < х,₂) ^ ^ < х/₅ч и Me = х_Ме = х@у

Если число наблюдений нечетное, п = 2р + 1, где р = 1, 2, то Me = x_med = x_(p+iy

Если число наблюдений четное, п = 2р, то Me = x_med = = ^{р р}. Например, при п = 6, x_med = —^;—-——.

Для интервального вариационного ряда медианным называют первый интервал [а_Ме; Ь_Ме), для которого накопленная частота превышает ноло;

п

вину объема наблюдений, т. е. :

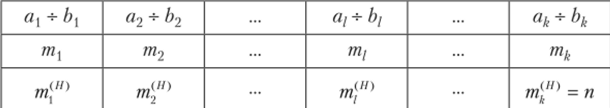
Здесь: т^Н)=т_г т^Н) =т_{ +т₂, …, ш_/^(//) =m^[⁾+w_/, …, т[^Н) =п, т. е. т^Н) =.

V¹ (Н)М (Н) м

= J/n_l=n И <-^;

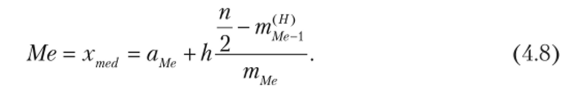
где а_Ме — нижняя граница медианного интервала; т^__{ — накопленная частота интервала, предшествующего медианному; h = (b_t -a_t) — ширина интервала группирования.

Свойство медианы, сумма абсолютных отклонений признака от Me меньше, чем от любой другой величины.

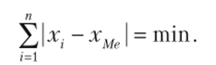
Мода — наиболее часто встречаемое значение признака.

Для интервального сгруппированного вариационного ряда мода.

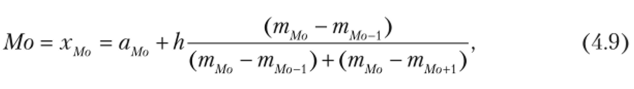
где а_Мо — нижняя граница модального интервала (рис. 4.14); т_Мо — частота модального интервала; т_{Мо Х} — частота интервала, предшествующего модальному; т.. — частота интервала, следующего за модальным.

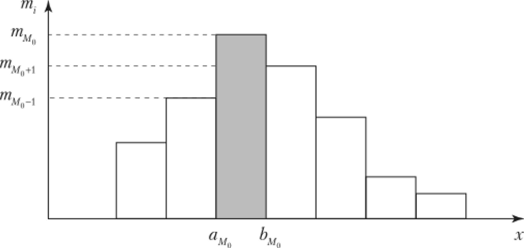
Рис. 4.14. Модальный интервал.

Пример 4.11.

На раскрой каждого из 8 костюмов на фабрике затрачено соответственно 60, 55, 50, 52, 45, 49, 58 и 46 мин. Определите медиану.

Данные не сгруппированы. Для определения медианы построим вариационный ряд.

Число наблюдений четно, поэтому медиана находится как среднее арифметическое двух средних значений: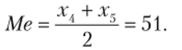

На основе интервального вариационного ряда объемов производства предприятий легкой промышленности, представленного в таблице примера 4.10, вычислите моду и медиану.

По вариационному ряду мода и медиана рассчитываются по формулам (4.8), (4.9).

Модальный интервал здесь — [104; 106], так как т₂ = 14 — наибольшая.

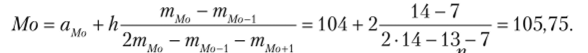
Медианный интервал — [ 106; 108], так как т^^!1) = 34 > ^ = 25;

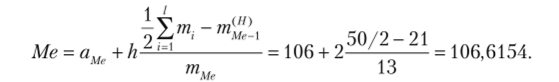
Формулы для расчета основных характеристик центра группирования данных приведены в табл. 4.12.