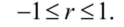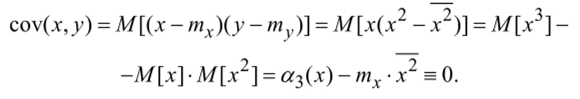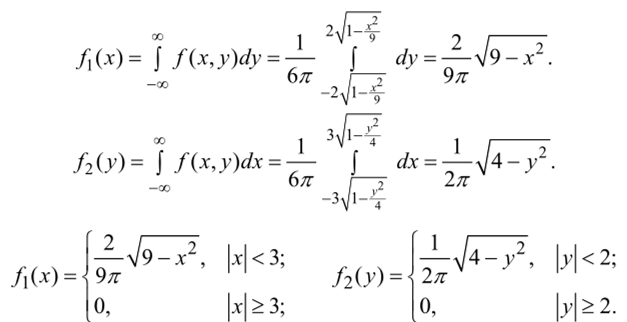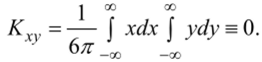Свойства коэффициента корреляции

1. Коэффициент корреляции принимает значения на отрезке [-1, 1]:

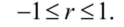(5.31).

• 2. Если случайные величины независимы, то их коэффициент корреляции равен нулю. Справедливость этого свойства очевидна, если учесть выражение (5.28), так как в этом случае К_ху = 0.
• 3. Равенство нулю коэффициента корреляции — необходимое, но недостаточное условие независимости случайных величин.

Из независимости случайных величин вытекает их некоррелированность. Обратное не всегда верно. Убедимся в этом на примере.

ПРИМЕР 4. Имеются две СВ: X => т_х — 0, #з (х) = 0; Y — х². Докажите, что эти величины некоррелированные.

РЕШЕНИЕ. Вычислим ковариацию: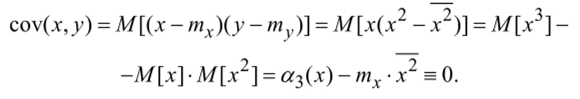

На практике для /7-мерного случайного вектора X = (^,<^₂, …, ?") достаточно сложно найти закон распределения (интегральную функцию, плотность распределения и т. п.). Поэтому обычно указывают п математических ожиданий М[^], М[?₂М[?"], п дисперсий D[?,], D[?], •••, D[%_n] и «-1 корреляционных моментов (гФ j),

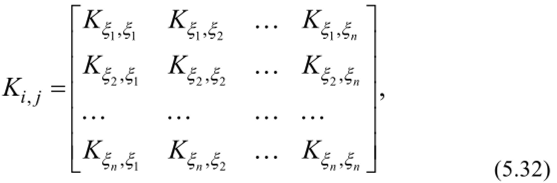
характеризующих парные корреляции всех величин, составляющих вектор X. Все корреляционные моменты, дополненные дисперсиями К= = (/ = 1, 2, …, «), располагают в виде матрицы:

которую называют корреляционной матрицей системы случайных величин.

Замечание. Корреляционная матрица симметрична относительно главной диагонали (см. формулы (5.26) и (5.27)).

ПРИМЕР 5. Двумерная СВ (X, Y) задана дифференциальной функцией:

Докажите, что X и Y — зависимые и некоррелированные СВ.

РЕШЕНИЕ. Зная двумерную плотность распределения, вычислим одномерные плотности:

Так как f (х, у) — /вл ^ f_x{x)? f₂(y), то X и Y- зависимые вели;

00 00.

чины. Найдем ковариацию: К_ху = J J (x-m_x)(y-m_Y)f (x, y) dxdy. Так.

— ОС -00.

как /{х)~ функция симметричная относительно OY, то т_х — 0, аналогично УПу — 0. Учитывая эти результаты, получим:

Действительно, каждый интеграл от нечетной функции в симметричных пределах равен нулю. Таким образом, СВ X и Y — зависимые и некоррелируемые.