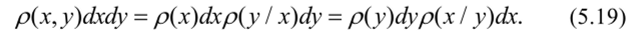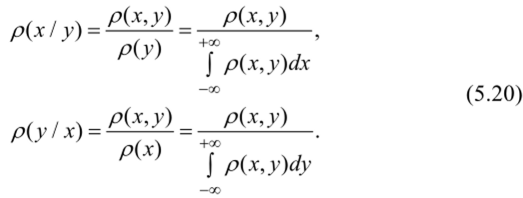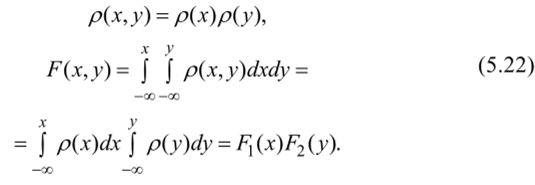Условная плотность распределения

Рассмотрим другой подход при определении вероятности попадания двумерной СВ в элементарный прямоугольник со сторонами Ах и Дуй устремим Ах и, А у к нулю (рис. 5.3).

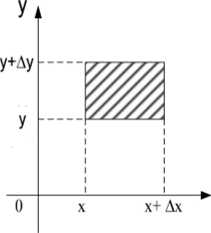
Рис. 5.3. Вероятность попадания в прямоугольник

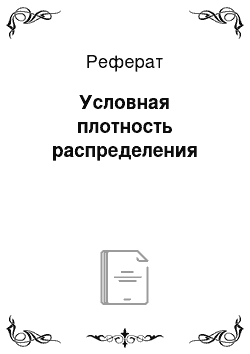
Рассмотрим вероятность попадания в элементарный прямоугольник как произведение вероятности попадания в бесконечную по аргументу у полосу [х, х + Ах], равную p (x)dx, на вероятность попасть в полосу [у, 7 + Ду] при условии, что аргумент х попал в полосу [x, x + А .г] - р (у / x) dy. В связи с тем, что аргументы х и у равносильны, запишем:

Таким образом, двумерная плотность распределения равна произведению одномерных плотностей распределения, одна из которых условная. Отсюда следует, что условная плотность распределения равна:

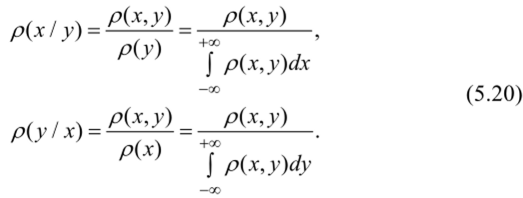
Случайная величина не зависит от другой случайной величины, если безусловная плотность распределения этой величины равна условной плотности распределения:

В этом случае говорят, что случайные величины X и Устатист и чески независим ы.

При независимости случайных величин X и У плотность распределения двумерной СВ (5.19) равна произведению плотностей соответствующих одномерных СВ, а интегральная функция распределения двумерной СВ равна произведению одномерных функций: