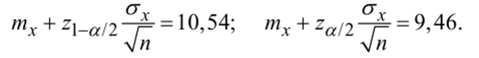Статистические критерии. 
Теория вероятностей и математическая статистика

Прежде чем перейти к рассмотрению понятия статистической гипотезы, сформулируем так называемый принцип практической уверенности, лежащий в основе применения выводов и рекомендаций, полученных с помощью теории вероятностей и математической статистики.

Если вероятность события, А в данном испытании очень мала, то при однократном испытании можно быть уверенным в том, что событие, А не произойдет, и в практической деятельности вести себя так, как будто событие, А вообще невозможно.

Вопрос о том, насколько малой должна быть вероятность а события А, чтобы его можно было считать практически невозможным, выходит за рамки математической теории и решается в каждом отдельном случае с учетом важности последствий, вытекающих из наступления события А. В ряде случаев можно пренебречь событиями, вероятность которых меньше 0,05, а в других, когда речь идет, например, о разрушении сооружений, гибели судна и т. п., нельзя пренебрегать событиями, которые могут появиться с вероятностью, равной 0,001.

Статистическим критерием (или просто критерием) называют случайную величину К, которая служит для проверки гипотезы.

Критерии значимости (критерии проверки гипотез, иногда просто тесты) — эго простейшие, но наиболее широко используемые статистические средства.

Критерий значимости даст возможность статистику найти разумный ответ па вопрос, подобный следующим:

• • Сталь, произведенная разными методами, имеет неодинаковые пределы прочности. «Указывает ли это на то, что производимая разными методами сталь имеет различную прочность или же выявленное различие можно объяснить выборочными флуктуациями?»
• • «Превосходит ли по эффективности одно противогриппозное средство другое?»
• • «Способствует ли отказ от курения снижению вероятности раковых заболеваний?»
• • «Превосходит ли по воздействию одно удобрение другое при выращивании овощей?»

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Рассмотрим простейший вид статистической процедуры, называемой проверкой гипотез. Пусть дана некоторая оценка ф, построенная по выборке из п независимых наблюдений СВ X. Предположим, что есть основания считать истинное значение оцениваемого параметра равным <�р₀. Однако, даже если истинное значение параметра (р равно (p_Q, выборочное значение ф, вероятно, не будет в точности равняться ^>₀, из-за выборочной изменчивости, присущей ф. Поэтому сформулируем следующий вопрос. Если предположить, что (p = (p_Q, то при каком отклонении ф от ср_й эта гипотеза должна быть отвергнута как несостоятельная? На этот вопрос ответ можно дать в статистических терминах, вычислив вероятность любого значимого отклонения ф от <�р₀ по выборочному распределению ф. Если вероятность такого отличия мала, то отличие следует считать значимым и гипотеза (р = (Ро должна быть отвергнута. Если же вероятность такого отличия велика, то отклонение следует приписать естественной статистической изменчивости и гипотеза (р = может быть принята.

Проиллюстрируем общий подход, предположив, что выборочное значение ф, являющееся оценкой параметра <�р, имеет плотность вероятности нормального распределения р (ф). Теперь, если гипотеза (р-<�Ро верна, то р (ф) должна иметь среднее значение (р₀ (рис. 10.1).

Вероятность а, использованная при испытании гипотез, называется уровнем значимости критерия.

Вероятность того, что ф окажется меньше нижней границы <�р_а/2, равна вероятности того, что ф превзойдет верхнюю границу ^__а/2 и каждая из них равна а / 2. Следовательно, вероятность того, что ф окажется вне интервала, заключенного между этими границами, равна а. Область значений ф, при которых гипотеза принимается, называется областью принятия гипотезы.

Нулевой (основной) называют выдвинутую гипотезу Н₀. В данном примере Hq. (р = (р^.

Область значений ф, при которых гипотеза должна быть отвергнута, называется областью отклонения гипотезы, или критической областью.

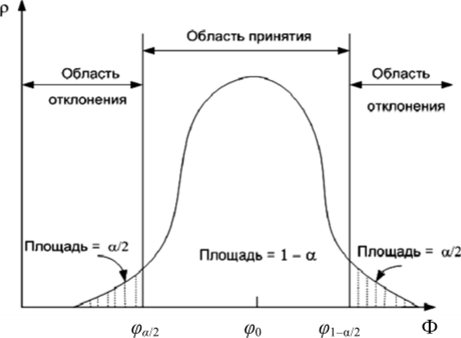
Рис. 10.1. Область принятия и отклонения гипотезы (двусторонний критерий)

Конкурирующей (альтернативной) называют гипотезу, которая противоречит нулевой. В данном примере Ну. (р^ср^.

Рассмотренный нами простой критерий испытания гипотез называется двусторонним критерием, так как, когда гипотеза неверна, значение (р может быть либо больше, либо меньше щ.

В ряде случаев достаточно бывает односторонних критериев (рис. 10.2). Например, пусть основная гипотеза Н₀: (р><�Рц. Тогда альтернативная гипотеза: Ну. <�р<(рц. Следовательно, в критерии должна использоваться только нижняя (левая) граница <�р_а, определяемая по плотности вероятности р (ф).

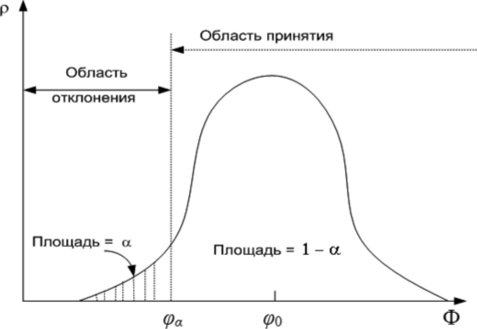
Рис. 10.2. Область принятия и отклонения гипотезы (односторонний критерий)

При проверке гипотезы возможны два типа ошибок.

• • Во-первых, гипотеза может быть отклонена, хотя фактически она верна. Такая ошибка называется ошибкой первого рода.
• • Во-вторых, гипотеза может быть принята, хотя фактически она неверна. Такая ошибка называется ошибкой второго рода.

Проиллюстрируем эти понятия графически (рис. 10.3).

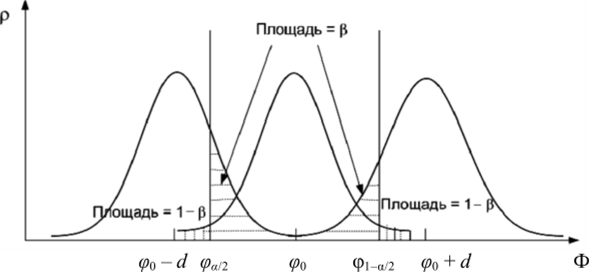
Рис. 10.3. Определение ошибки первого и второго рода при проверке гипотез

Из рисунка видно, что ошибка первого рода происходит в том случае, когда при справедливости гипотезы Н₀ значение ф попадает в область ее отклонения (критическую область). Следовательно, вероятность ошибки первого рода равна а — уровню значимости критерия.

Для определения вероятности ошибки второго рода предположим, к примеру, что истинный параметр равен либо (p₀ + d, либо (p₀-d (см. рис. 10.3). Если гипотеза состоит в том, что Н₀: (р = <�Ро, тогда как на самом деле <�р = ср₀ ± d, то вероятность того, что ф попадает в область принятия гипотезы, заключенную между <�р_а/2 и <�Р__а/2, равна Д. Следовательно, вероятность ошибки второго рода равна Д при выявлении отклонения величиной ±d от гипотетического значения (р₀.

Вероятность 1-Д называется мощностью критерия.

Следует отметить, что вероятности ошибок первого и второго рода вычисляются при разных предположениях о распределении (если верна гипотеза Н₀ и если верна гипотеза Н_]), так что никаких раз и навсегда фиксированных соотношений (например а = 1 — Д, независимо от вида гипотезы и вида критерия) между ними нет. Таким образом, при фиксированном объеме выборки п мы можем сколь угодно уменьшать ошибку первого рода, уменьшая уровень значимости а. При этом, естественно, возрастает вероятность (3 — ошибки второго рода (уменьшается мощность критерия). Единственный способ одновременно уменьшить ошибки первого и второго рода (а и /3) — увеличить размер выборки п. Именно такие соображения лежат в основе выбора нужного размера выборки в статистических экспериментах.

ПРИМЕР 1. Построение критерия проверки гипотез.

Предположим, что среднее значение СВ X равно т_х = 10, также л.

предположим, что дисперсия известна и равна сг_х = 4. Необходимо найти объем выборки п, позволяющий построить критерий проверки гипотезы #₀: т_х-10 с 5%-м уровнем значимости и 5%-й ошибкой второго рода для выявления 10%-х отклонений от гипотетического значения. Построим также область принятия гипотезы Н₀.

РЕШЕНИЕ. Выборочное среднее х, определяемое формулой (8.6), является несмещенной оценкой т_х. Соответствующее выборочное распределение х определяется из соотношения (9.7):

где z имеет распределение N (0,1). Верхняя и нижняя границы области принятия гипотезы соответственно равны:

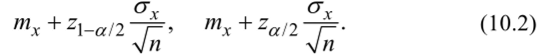
Если теперь истинное среднее значение равно т'_х = т_х ±d, то с вероятностью (3 произойдет ошибка второго рода, если выборочное среднее х окажется меньше (левее) верхней границы и больше (правее) нижней. В терминах выборочного распределения х со средним т'_х = т_х + d или.

т_х = т_х — d для верхней и нижней границ (рис. 10.3):

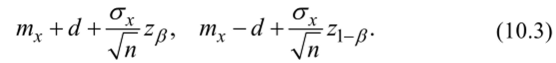
Итак, справедливы следующие равенства:

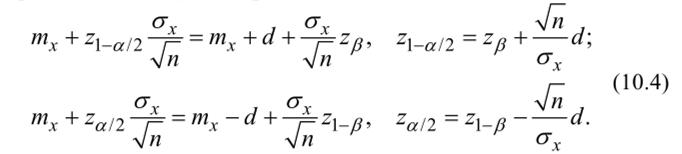
Вспомним, что благодаря симметричности распределения N (0,1) справедливы равенства:

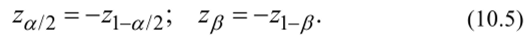
Теперь из (10.4) с учетом (10.5) найдем требуемый объем выборки:

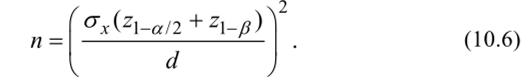
Для конкретных значений данного примера: сг_х.=2, = 0,1−10 = 1,.

^zl-a/2 ^{= г}0,975 ⁼ 1"96; Z-p =^о, 95 ⁼ 1"645. Подставим эти значения в (10.6) и получим значение необходимого объема выборки и = 51,9841. Таким образом, объем выборки должен быть равен или больше пятидесяти двух. Область принятия гипотезы Н₀ определяется соответствующими границами (верхней и нижней (10.2)):