Используемые обозначения и основные формулы

Глава 3. Сводка и группировка статистических данных Используемые обозначения

п — число групп;

N — число единиц совокупности; h — величина (шаг) интервала;

R — размах вариации;

^Хтх ~ максимальное значение признака в совокупности;

^min ^— минимальное значение признака в совокупности; о — среднее квадратическое отклонение;

Rq — квартальный размах;

а — константа; для прогрессивно возрастающих интервалов а > 0, для прогрессивно убывающих а < 0;

q — константа; для прогрессивно возрастающих интервалов q > 1, для прогрессивно убывающих q < 1, всегда положительное число;

fi — частота; w, — частость.

Основные формулы

Формула Стерджеса.

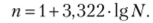
Величина равного интервала.

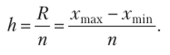
Формула Скотта.

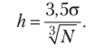
Формула Фридмана и Диакониса.

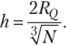
Размах вариации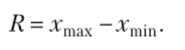

Величина неравного интервала:

• • при арифметической прогрессии h_i+1 = h_t + а
• • при геометрической прогрессии h_i+l =h_rq.

Плотность распределения:

• абсолютная //=т" ;

К

Г щ

• относительная /",=—.

hi

Глава 5. Обобщающие статистические показатели Используемые обозначения

fi — частота, показывающая, сколько раз встречается значение признака;

h — величина интервала;

/7 — объем совокупности (сумма частот);

Xj — варианта, отдельное значение признака в статистической совокупности;

х₀ — условный нуль, в качестве которого принимается середина интервала с наибольшей частотой; z — показатель степени.

Основные формулы

Относительная величина планового задания 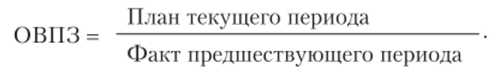Относительная величина выполнения плана Относительная величина динамики.

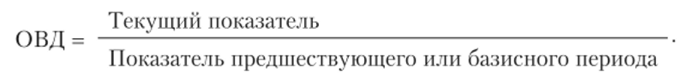
Взаимосвязь между относительными величинами планового задания, выполнения плана и динамики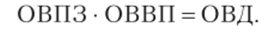

Относительная величина структуры 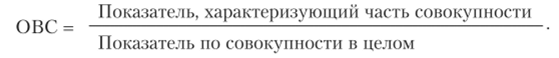Относительная величина координации 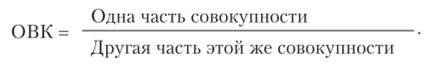Относительная величина сравнения 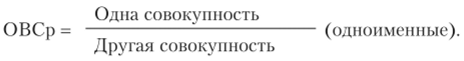Относительная величина интенсивности 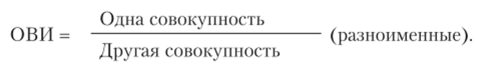Степенная средняя простая.

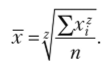
Степенная средняя взвешенная.

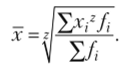
Средняя арифметическая простая.

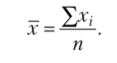
Средняя арифметическая взвешенная.

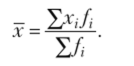
Упрощенная формула расчета средней арифметической.

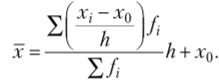
Средняя геометрическая простая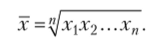

Средняя геометрическая взвешенная 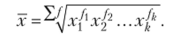Средняя гармоническая простая.

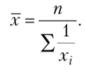
Средняя гармоническая взвешенная.

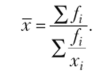
Средняя квадратическая простая 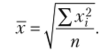Средняя квадратическая взвешенная 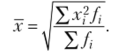Средняя кубическая простая 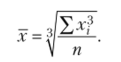Средняя кубическая взвешенная.

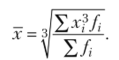
Правило мажорантности средних.

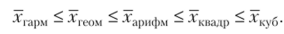
Глава 6. Анализ вариации Используемые обозначения

р, — вероятности вариант единиц статистической совокупности; Pes — доля (в процентах) количества значений признака, лежащих в интервале, равном половине среднего квадратического отклонения;

cIq — значение квартального отклонения;

V_c — значение коэффициента вариации;

V_R — значение коэффициента осцилляции;

Vj — значение линейного коэффициента вариации;

Л () — значение межквартильного интервала;

Д — значение первой децили;

Qi — значение первой квартили;

К_х — значение первой квинтили;

Щ — значение первой квинтцентили;

— значение первой сикстили;

Vq — значение показателя квартильной вариации;

Xj — значение признака;

R — значение размаха вариации;

/пр — значение среднего линейного отклонения для несгрупированных данных;

/вз — значение среднего линейного отклонения для сгрупированиых данных;

I — значение среднего линейного отклонения;

Хфифм — значение средней арифметической;

<2з — значение третьей квартили;

*_тах — максимальное значение признака; ^ximn — минимальное значение признака;

/q — накопленная частота в интервале, предшествующему первому квартильному интервалу;

— накопленная частота в интервале, предшествующему третьему квартильному интервалу;

/мс₁ ^— накопленная частота домедианного интервала; ^хш — нижняя граница медианного интервала; ^хш — нижняя граница модального интервала;

Xq_{ — нижняя граница первого квартильного интервала;

Xqz — нижняя граница третьего квартильного интервала; х — среднее значение признака для изучаемой совокупности; Yjfi — сумма частот ряда распределения;

Pas — удельный вес (в процентах) количества тех значений признака, которые превосходят среднюю арифметическую, в общем количестве значений признака данного ряда;

Рз — центральный момент третьего порядка;

М-4 — центральный момент четвертого порядка;

/мо_! — частота домодального интервала;

/мс ^— частота медианного интервала;

/мо — частота модального интервала;

/q, — частота первого квартильного интервала;

/м₀₊₁ — частота послемодального интервала;

/<2з — частота третьего квартильного интервала;

J — число единиц совокупности в отдельной группе;

APj — абсолютная плотность; h² — величина интервала значений признака; wf — значение частости в качестве процентов; тщ — значение частости как доли единицы;

К"._ш — коэффициент изменчивости категорий;

/^н_Дм ^— накопленная частота в интервале, предшествующему первому децильному интервалу;

fⁿK. — накопленная частота в интервале, предшествующему первому квинтильному интервалу;

1^пЩ- — накопленная частота в интервале, предшествующему первому квинтцентильному интервалу;

/^H5j_, — накопленная частота в интервале, предшествующему первому сикстильному интервалу;

Х_Лх — нижняя граница первого децильиого интервала;

Х_К{ — нижняя граница первого квинтильного интервала;

Хщ — нижняя граница первого квинтцентильного интервала; X_S[ — нижняя граница первого сикстильного интервала;

OPj — относительная плотность;

/д, — частота первого децильиого интервала;

/к_{ — частота первого квинтильного интервала;

/щ — частота первого квинтцентильного интервала; fs_{ — частота первого сикстильного интервала;

M_k — эмпирический момент^-го порядка; а — значение среднего квадратического отклонения; а_вз — значение среднего квадратического отклонения для сгрупированных данных;

а_пр — значение среднего квадратического отклонения для несгрупированных данных;

ft — частоты вариационного ряда;

Н —абсолютный показатель энтропии; h — ширина интервала; k — степень отклонения (порядок момента);

^—количество категорий признака;

Me — значение медианы;

Мо — значение моды; п — число единиц совокупности;

Q₂ — значение второй квартили распределения;

Wj — частоты вариационного ряда;

X; — значение признака;

А — величина, от которой определяются отклонения.

Основные формулы Средняя арифметическая простая.

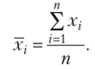
Средняя арифметическая взвешенная 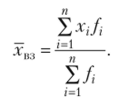Частость.

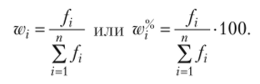
Абсолютная плотность распределения 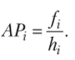Относительная плотность распределения 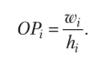Эмпирический момент k-ro порядка.

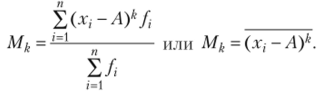
Начальный момент /г-го порядка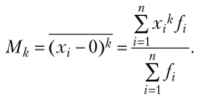

Условный момент k-то порядка 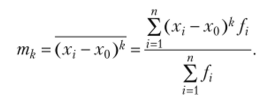Центральный момент k-ro порядка.

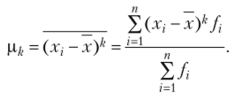
Медиана в вариационном ряду с непрерывным признаком 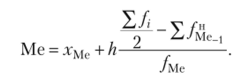Первая квартиль.

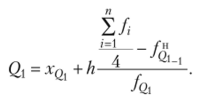
Третья квартиль.

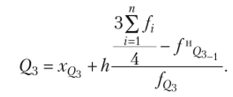
Межквартильный интервал (размах).

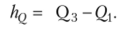
Первая квинтиль.

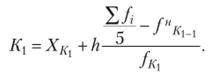
Первая сикстиль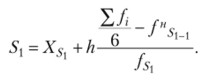

Первая дециль 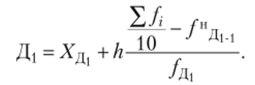Первая квинтцентиль.

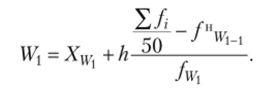
Мода в вариационном ряду с непрерывным признаком.

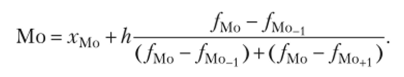
Приближенные соотношения между средней арифметической, медианой и модой.

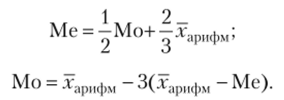
Размах вариации 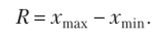Квартильное отклонение.

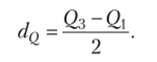
Среднее линейное отклонение для несгрупированных данных 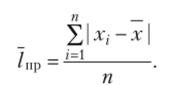Среднее линейное отклонение для сгрупированных данных.

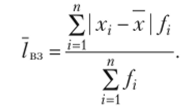
Среднее квадратическое отклонение для несгрупированных данных.

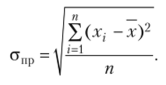
Среднее квадратическое отклонение для сгрупированных данных.

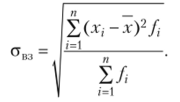
Дисперсия для несгрупированных данных 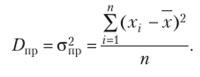Дисперсия для сгрупированных данных.

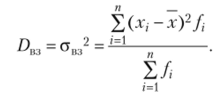
Разница между дисперсиями (поправка Шеппарда).

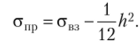
Упрощенный способ расчета дисперсии 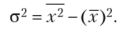Абсолютный показатель энтропии.

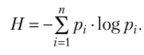
Относительный показатель энтропии.

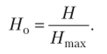
Коэффициент изменчивости категорий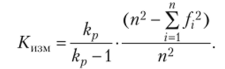

Коэффициент осцилляции 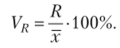Линейный коэффициент вариации.

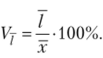
Коэффициент вариации.

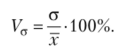
Относительный показатель квартильной вариации 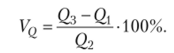Коэффициенты асимметрии Пирсона 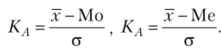Коэффициент асимметрии 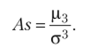Центральный момент третьего порядка.

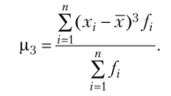
Показатель средней квадратической ошибки коэффициента асимметрии.

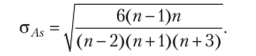
Показатель эксцесса распределения.

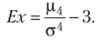
Центральный момент четвертого порядка.

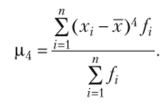
Показатель средней квадратической ошибки коэффициента эксцесса.

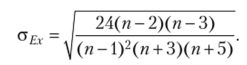
Упрощенная формула коэффициента асимметрии Линдберга 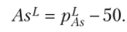Упрощенная формула показателя эксцесса Линдберга.

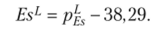
Глава 7. Статистический анализ структуры совокупности и ее изменений.

Используемые обозначения

dji, djo — удельные веса отдельных элементов двух сравниваемых совокупностей;

k — количество элементов (групп) в совокупности; yj — доля доходову-й группы;

X: — доля населения у-й группы; сит у: — накопленные доли доходов.

Основные формулы

Сумма абсолютных изменений удельных весов 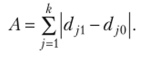Индекс различий.

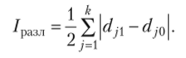
Интегральный коэффициент структурных сдвигов Гатева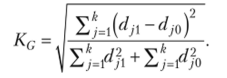

Индекс структурных различий Салаи 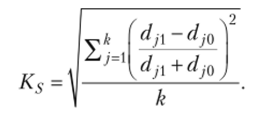Индекс Рябцева.

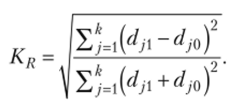
Среднее линейное изменение долей 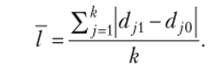Среднее квадратическое изменение.

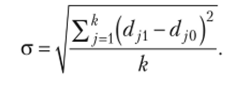
Среднее относительное линейное изменение.

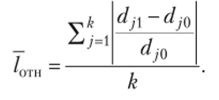
Коэффициент Лоренца 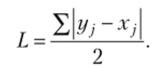Коэффициент Джини.

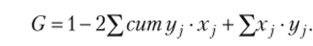
Глава 8. Основы выборочного наблюдения Используемые обозначения

N — генеральная совокупность; п — выборочная совокупность;

t — доверительный коэффициент, связанный с вероятностью (см. таблицу интеграла Лапласа);

р — средняя ошибка выборки;

Д — предельная ошибка выборки;

of — внутригрупповая (остаточная) дисперсия;

S² — межгрупповая (факторная) дисперсия;

pq — дисперсия альтернативных дихотомических признаков;

R — количество серий (гнезд) в генеральной совокупности; г — количество серий (гнезд) в выборочной совокупности;

Я₀, Я) — нулевая (проверяемая) и конкурирующая (альтернативная) гипотезы;

а, (3 — ошибки I и II рода;

Т; V, х²; F — критерии, применяемые для проверки разных гипотез.

Основные формулы

Средние квадратические ошибки (стандартные погрешности) некоторых выборочных характеристик

Параметр	Средние квадратические ошибки о.

Формулы предельной ошибки и необходимого объема выборки для различных случаев отбора

	Выборка.	Собственно-случайная.		Типическая.		Серийная.
		повторная.	бесновторная.	повторная.	бесновторная.	повторная.	бесновторная.
Предельная ошибка, Д.	средней, х
	доли, Р
Необходимая численность, п	средней, х
	доли, Р

Основные формулы для проверки статистических гипотез

Гипотеза.	Выборочная статистика.	Распределение.	Замечания.
		Стыодента с Ксв = п -1 степенями свободы.
		Стыодента с Ксв = щ+п2— 2 степенями свободы.
		X2 распределение с Ксв — yi~ 1 степенями свободы.

Гипотеза.	Выборочная статистика.	Распределение.	Замечания.
Критерий согласия Пирсона.		Распределение х2 для JV(0количество степеней свободы v = s — (2 +1).