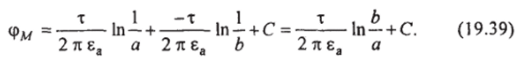Поле двух параллельных заряженных осей
Пусть одна ось на единицу длины имеет заряд +т, другая — зарядт. Возьмем в поле произвольную точку М (рис. 19.14). Результирующая напряженность поля в ней Ем равна геометрической сумме напряженностей от обоих зарядов. Расстояние отточки Мдо положительно заряженной оси обозначим через а, до отрицательно заряженной оси — через Ь. Потенциал есть функция скалярная. Потенциал точки М равен сумме… Читать ещё >
Поле двух параллельных заряженных осей (реферат, курсовая, диплом, контрольная)
Пусть одна ось на единицу длины имеет заряд +т, другая — зарядт. Возьмем в поле произвольную точку М (рис. 19.14). Результирующая напряженность поля в ней Ем равна геометрической сумме напряженностей от обоих зарядов. Расстояние отточки Мдо положительно заряженной оси обозначим через а, до отрицательно заряженной оси — через Ь. Потенциал есть функция скалярная. Потенциал точки М равен сумме потенциалов от каждой оси:
*> Единица, находящаяся под знаком логарифма в (19.38), имеет смысл единичного радиуса (единицы измерения), поэтому логарифм берется от величины с нулевой размерностью.
Уравнением эквипотенциали в поле двух заряженных осей является выражение b/a = const. Эквипотенциаль представляет собой совокупность точек, отношение расстояний в которых до двух заданных точек есть величина постоянная.
Рис. 19.14.
В геометрии известна теорема Апполония. Согласно этой теореме геометрическим местом точек, отношение расстояний которых до двух заданных точек есть величина постоянная, является окружность. Поэтому эквипотенциаль в поле двух заряженных осей есть окружность. Рассмотрим, как ее можно построить. Соединим точку М с осями. Проведем биссектрисы внутреннего (аМЬ) и внешнего (рМа) уг;
лов. Точки / и 2 пересечения биссектрис с линией, проведенной через заряженные оси, и точка М будут тремя точками искомой окружности.
Для нахождения положения центра окружности (точки О) разделим пополам расстояние между точками / и 2.